Введение
В работах авторов Калантарова П.Л., Цейтлина Л.А. и др. были решены частные случаи расчета индуктивностей канонических форм, прямолинейных и криволинейных проводов, плоских контуров, круговых колец и т.д., а также предложены приближенные и аналитические методы расчета индуктивностей для ограниченных классов задач, где постоянно требуется обращение к приведенным таблицам и кривым, что является неудобным. Технология приведенных методов заключалась в том, что необходимо подсчитывать отдельно собственные и взаимные индуктивности, затем их складывать, где неизбежно содержались эллиптические интегралы, в связи с этим и возникала необходимость в дополнительных справочных данных [6].
В случае с емкостью конденсатора сложной конфигурации и неоднородной диэлектрической проницаемостью традиционными методами необходимо рассчитывать емкости каждых однородных слоев по отдельности, затем их складывать или воспользоваться интегрированием, что также является весьма неудобным, если конденсатор содержит большое количество слоев неоднородности [8]. Поэтому расчет индуктивностей и емкостей с помощью компьютерного моделирования является актуальной задачей.
Методика
Для расчета статических электромагнитных полей [4] и параметров использовалась программа COMSOL Multiphysics (рис. 1).
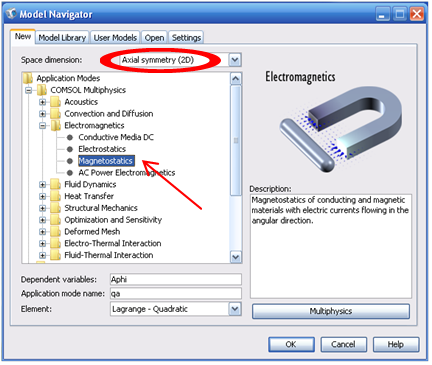
Рис. 1. Навигатор моделей COMSOL Multiphysics
В данной работе предлагается энергетический метод расчета параметров, где полученная через энергию магнитного поля результирующая индуктивность содержит в себе как собственные индуктивности элементов электродной системы, так и взаимные индуктивности между элементами системы. Полученная через энергию электрического поля результирующая емкость конденсатора с различной диэлектрической проницаемостью содержит все емкости от каждых слоев неоднородности по отдельности.
Из навигатора моделей COMSOL Multiphysics, представленного на рисунке 1, очевидно, что для моделирования магнитостатического поля и расчета индуктивности необходим блок «Magnetostatics» (магнитостатика) и, соответственно, для моделирования электростатического поля и расчета емкости необходим блок «Electrostatics» (электростатика).
Экспериментальная часть
Апробация метода была произведена на примере кругового кольца кругового сечения [1, 6] и сферического конденсатора со слоистой диэлектрической проницаемостью [2, 7]. На рисунке 2 представлено объемное изображение кругового кольца кругового сечения (а) с радиусом сечения кольца 
м, площадью сечения 
м2, а также сферического конденсатора (б) с радиусами 
м и диэлектрическими проницаемостями 
(начиная с окружности меньшего радиуса).
а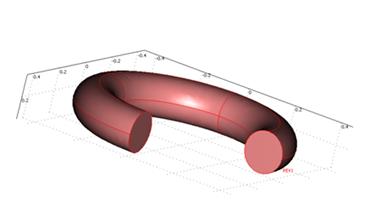 
б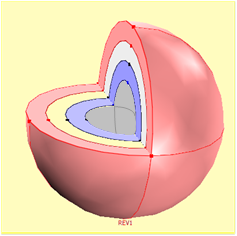 
Рис. 2. Объемное изображение: а) кругового кольца кругового сечения; б) сферического конденсатора со слоистой диэлектрической проницаемостью
В COMSOL Multiphysics необходимо выбрать границы поля и шаг сетки, затем построить геометрию кругового кольца и сферического конденсатора соответственно, указав необходимые магнитные (плотность тока, магнитная проницаемость) и электрические (разность потенциалов, диэлектрическая проницаемость) параметры. Зная геометрию и размеры исследуемых моделей, было получено распределение статических электромагнитных полей и расчет соответствующих параметров [5].
Энергия магнитного поля:
, (1)
здесь 
– ток, 
– энергия магнитного поля, 
– индуктивность.
Энергия электрического поля:
, (2)
здесь 
– напряжение, 
– энергия электрического поля, 
– емкость.
На рисунке 3 представлено распределение магнитостатического поля кругового кольца (а) и электростатическое поле сферического конденсатора со слоистой диэлектрической проницаемостью (б).
Подробный анализ расчета индуктивности на основе расчета энергии магнитного поля был рассмотрен в [3].
а 
б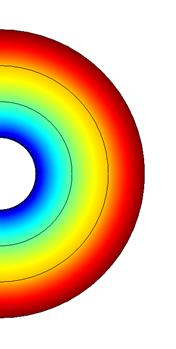 
Рис. 3. Распределение статических электромагнитных полей: а) кругового кольца кругового сечения; б) сферического конденсатора со слоистой диэлектрической проницаемостью
При токе 
А, используя (1), получаем формулу для индуктивности 
. В соответствии с этим (рис. 4) рассчитаем индуктивность.
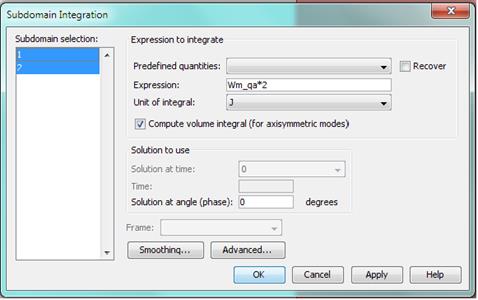
Рис. 4. Запись уравнения в окне Subdomain Integration для расчета индуктивности
В результате получили индуктивность кругового кольца, равную 
Гн.
Далее на основе [2] сравним полученный результат расчета индуктивности с расчетом в среде MathCAD, используя формулу:
, (3)
где 
м – радиус кольца, 
Гн/м – магнитная постоянная.
В результате получили индуктивность кругового кольца, равную 
Гн.
Погрешность между расчетами в программах COMSOL Multiphysics и MathCAD (3) составляет 0,9%, что говорит об адекватности моделирования.
При напряжении 
В, используя (2), получаем формулу для емкости 
. В соответствии с этим рассчитаем емкость, где на основе рисунка 4 в поле «Expression» необходимо ввести формулу для расчета результирующей емкости «We_es*2». В качестве «Unit of integral» (единицы интегрирования) выбрать J – «Electric energy density» (плотность электрической энергии).
В результате получили емкость сферического конденсатора, равную 
Ф.
Далее на основе [8] сравним полученный результат расчета емкости с расчетом в среде MathCAD, используя формулу:
; 
, 
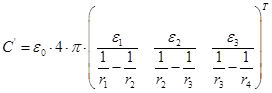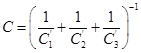(4)
где 
Ф – емкости каждых слоев конденсатора по отдельности (начиная с окружности меньшего радиуса); 
Гн/м – диэлектрическая постоянная.
В результате получили емкость, равную 
Ф.
Погрешность между расчетами в программах COMSOL Multiphysics и MathCAD (4) составляет 0,1%, что говорит об адекватности моделирования.
Результаты
Таким образом, используя программу COMSOL Multiphysics, можно одновременно получить распределение статических электромагнитных полей и соответствующие значения параметров, таких как индуктивность катушки и емкость конденсатора различной конфигурации. Преимущество данного способа – в том, что расчет можно производить не только в декартовой системе, но и в цилиндрической или сферической системах координат.
Рецензенты:
Сивков А.А., д.т.н., профессор кафедры ЭПП ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.
Курец В.И., д.т.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.