Введение
Регулирование напряжения силовых трансформаторов осуществляется путем механического переключения отпаек обмотки (РПН и ПБВ). Этот способ регулирования напряжения обладают рядом недостатков, таких как дискретность регулирования, невозможность компенсации реактивной мощности, износ трансформаторного масла и механических контактов и т.п. Ведется разработка альтернативных способов регулирования вторичных напряжений силовых трансформаторов. В [3] описан трансформаторно-тиристорный регулятор напряжения. В [2] рассматривается устройство для плавного регулирования вторичного напряжения силового трансформатора, содержащее ведомый сетью обратимый преобразователь, а также два автономных инвертора, работающих в 180–градусном режиме.
Материалы и методы исследования
На основании изложенных в [4] положений были разработаны несколько вариантов схем силовой части трансформатора с векторным управлением. Один их них представлен на рис. 1. Обмотка 4 служит для подключения нагрузки (сети низшего напряжения). Вольтодобавочный трансформатор 5 предназначен для согласования параметров силовых ключей преобразователя 11 с питающей сетью. Низкочастотные фильтры 8 и 9 представляют собой трехфазные Г – образные LC – фильтры. Конденсаторная батарея 13 звена постоянного тока 12 предназначена для обеспечения корректной работы преобразователей 10 и 11. Отличительной особенностью данной схемы, по сравнению с [2], является использование двух активных преобразователей в целях регулирования.
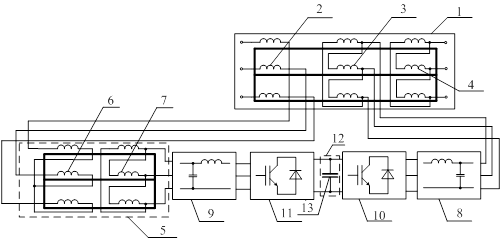
Рис. 1. Схема силовой части трансформатора с векторным управлением
1 – главный трансформатор; 2 – первичная обмотка; 3 – согласующая обмотка устройства векторного управления; 4 – вторичная обмотка; 5 – вольтодобавочный трансформатор; 6 и 7 – выходная и входная обмотки трансформатора 5 соответственно; 8 и 9 – низкочастотные фильтры; 10 и 11 – первичный и вторичный активные преобразователи соответственно; 12 – звено постоянного тока; 13 – конденсаторная батарея
При формировании базовой математической модели трансформатора с векторным управлением были приняты следующие допущения: трехфазная система симметрична; ключи активных преобразователей идеальны; потери активной мощности во всех элементах отсутствуют; намагничиванием сердечника и индуктивностями рассеяния трансформатора и питающей сети пренебрегаем.
Сделанные допущения позволяют выполнить исследование по схеме замещения для одной фазы. Звено, содержащее фильтры и активные преобразователи, заменено зависимыми источниками тока и напряжения с равными активными мощностями. При правильном подборе [5] параметров фильтров в этих источниках можно учитывать только основные гармоники. Схема замещения трансформатора с векторным регулированием показана на рис. 2.
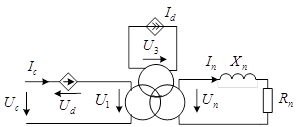
Рис. 2. Схема замещения трансформатора с векторным управлением
Закон полного тока для магнитной цепи силового трансформатора имеет вид
![]() , (1)
, (1)
где ![]() ,
, ![]() и
и ![]() – количество витков обмоток. Закон Кирхгофа для стороны высокого напряжения имеет вид
– количество витков обмоток. Закон Кирхгофа для стороны высокого напряжения имеет вид
![]() . (2)
. (2)
По уравнениям (1) и (2) строим векторные диаграммы для случаев, когда действующее значение напряжения нагрузки необходимо увеличить (рис. 3а) и уменьшить (рис. 3б). Из векторной диаграммы видно, что через преобразователи 10 и 11 (см. рис. 1) передается активная мощность. В случае, когда необходимо увеличить действующее значение напряжения нагрузки (рис. 3а), активная мощность передается от источника тока к источнику напряжения (рис. 3в). В этом случае преобразователь 10 работает в режиме выпрямления, а преобразователь 11 – в режиме инвертирования. Если необходимо уменьшить напряжение нагрузки (рис. 3б), то направление передачи активной мощности противоположное и преобразователь 11 работает в режиме выпрямления, а преобразователь 10 – в режиме инвертирования.
Напряжения нагрузки с требуемым действующим значением можно получить при различных величинах и фазах зависимого источника напряжения ![]() . Необходимая величина входного напряжения идеального трансформатора
. Необходимая величина входного напряжения идеального трансформатора ![]() показана на рис. 3 пунктирной окружностью 1. При заданной максимальной величине напряжения преобразователя (показана на рис. 3 окружностью 2) можно выбрать любой режим работы трансформатора, при котором геометрическим местом концов векторов
показана на рис. 3 пунктирной окружностью 1. При заданной максимальной величине напряжения преобразователя (показана на рис. 3 окружностью 2) можно выбрать любой режим работы трансформатора, при котором геометрическим местом концов векторов ![]() является часть окружности 1, находящаяся внутри области, ограниченной окружностью 2. Вариант, показанный на рис. 3а, обеспечивает наибольшую величину компенсации реактивной мощности активным преобразователем 11.
является часть окружности 1, находящаяся внутри области, ограниченной окружностью 2. Вариант, показанный на рис. 3а, обеспечивает наибольшую величину компенсации реактивной мощности активным преобразователем 11.
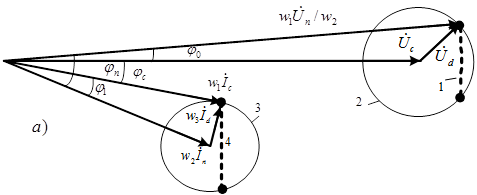
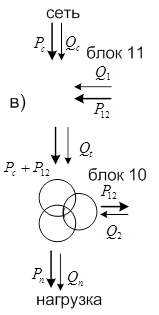
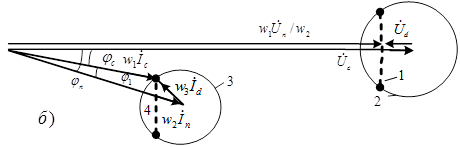
Рис. 3. Векторные диаграммы трансформатора при увеличении (а) и при уменьшении (б) напряжения нагрузки. Энергетическая диаграмма для трансформатора (в).
Величина и направление тока зависимого источника ![]() также могут быть выбраны неоднозначно. Выбор определяется выполнением баланса активных мощностей преобразователей 10 и 11 (пунктирная прямая на рис. 3) и максимально допустимой величиной тока преобразовательного блока 10 (окружность 3 на рис. 3). В этом случае геометрическим местом концов векторов
также могут быть выбраны неоднозначно. Выбор определяется выполнением баланса активных мощностей преобразователей 10 и 11 (пунктирная прямая на рис. 3) и максимально допустимой величиной тока преобразовательного блока 10 (окружность 3 на рис. 3). В этом случае геометрическим местом концов векторов ![]() является часть пунктирной прямой, ограниченная окружностью 3. Вариант, показанный на рис. 3а, обеспечивает наибольшую величину компенсации реактивной мощности активным преобразователем 10.
является часть пунктирной прямой, ограниченная окружностью 3. Вариант, показанный на рис. 3а, обеспечивает наибольшую величину компенсации реактивной мощности активным преобразователем 10.
В результате совместной работы преобразовательных блоков 10 и 11 было получено необходимое действующее значение напряжения нагрузки и выполнена частичная компенсация реактивной мощности нагрузки.
По векторной диаграмме (рис. 3а) получим математическую модель устройства. Фазу напряжения сети примем равной нулю. Зададим величины: ![]() (активная мощность нагрузки),
(активная мощность нагрузки), ![]() (сдвиг по фазе между током и напряжением нагрузки),
(сдвиг по фазе между током и напряжением нагрузки), ![]() (необходимое значение напряжения на нагрузке),
(необходимое значение напряжения на нагрузке), ![]() (действующее значение напряжения сети),
(действующее значение напряжения сети), ![]() ,
, ![]() и
и ![]() (количество витков обмоток),
(количество витков обмоток), ![]() и
и ![]() (действующие значения напряжения и тока зависимых источников). Возьмем величину
(действующие значения напряжения и тока зависимых источников). Возьмем величину ![]() в качестве параметра.
в качестве параметра.
Тогда действующие значение тока нагрузки и тока сети
![]() ,
, ![]() . (3)
. (3)
Из треугольника токов по диаграмме получаем
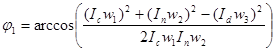 . (4)
. (4)
Из треугольника напряжений получаем
![]() (5)
(5)
![]() (6)
(6)
Векторная диаграмма (рис. 3а,б) или выражение (6) позволяют рассчитать диапазон регулирования напряжения нагрузки (![]() ,
, ![]() ) при неизменном значении
) при неизменном значении ![]() или диапазон колебаний напряжения сети (
или диапазон колебаний напряжения сети (![]() ,
, ![]() ) при стабилизации напряжения нагрузки
) при стабилизации напряжения нагрузки ![]() . Для максимально допустимого действующего значения напряжения источника
. Для максимально допустимого действующего значения напряжения источника ![]() диапазон стабилизации напряжения определяется выражениями
диапазон стабилизации напряжения определяется выражениями
![]() и
и ![]() . (7)
. (7)
Уравнения (3-6) позволяют получить аналитическое решение для параметра ![]() при заданных значениях
при заданных значениях ![]() из (6) и
из (6) и ![]() .
.
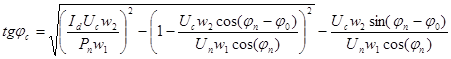 (8)
(8)
Выражение (8) определяет допустимый диапазон мощностей нагрузок, в котором можно осуществить регулирование или стабилизацию. Для максимально допустимого действующего значения тока источника ![]() диапазон мощностей определяется из выражений
диапазон мощностей определяется из выражений
![]() и
и ![]() (9)
(9)
Выражения (3-6) позволяют проанализировать энергетический баланс рассматриваемого устройства. Используя ![]() , получим активную и реактивную мощности, передаваемые через обмотку высокого напряжения
, получим активную и реактивную мощности, передаваемые через обмотку высокого напряжения
![]() ,
, ![]() . (10)
. (10)
Активная и реактивная мощности, потребляемые из сети
![]() ,
, ![]() . (11)
. (11)
Активная мощность, передаваемая от источника тока к источнику напряжения
![]() . (12)
. (12)
Реактивная мощность, генерируемая преобразовательными блоками 10 и 11, соответственно
![]() , (13)
, (13)
![]() . (14)
. (14)
Выражения (12) и (14) характеризуют также загрузку регулировочной обмотки силового трансформатора.
Результаты и их обсуждение
Используя полученную математическую модель, исследуем загрузку по активной и реактивной мощности различных частей рассматриваемого трансформатора в зависимости от изменения напряжения сети. Активная и реактивная мощность нормированы на активную мощность нагрузки ![]() , напряжение сети нормировано на номинальное значение. Обозначения зависимостей на рис. 4 соответствуют введенным обозначениям в выражениях (10-14). Максимально допустимые значения управляющих параметров выбраны удовлетворяющими условиям (7) и (9) при равномерной загрузке блоков 10 и 11.
, напряжение сети нормировано на номинальное значение. Обозначения зависимостей на рис. 4 соответствуют введенным обозначениям в выражениях (10-14). Максимально допустимые значения управляющих параметров выбраны удовлетворяющими условиям (7) и (9) при равномерной загрузке блоков 10 и 11.
Из рис. 4 следует, что во всем регулировочном диапазоне осуществляется компенсация реактивной мощности. Генерация реактивной мощности блоками 10 и 11 эффективна, поскольку оба блока генерируют емкостную мощность.
Величина реактивной мощности, генерируемой преобразовательными блоками, не всегда должна быть максимальной. Оптимизируя затраты на передачу реактивной мощности и затраты на выработку реактивной мощности преобразовательными блоками можно получить оптимальное значение реактивной мощности, отдаваемой в сеть. Если реактивная мощность нагрузки много больше указанного значения, то описанная выше стратегия выбора величин и фаз тока и напряжения зависимых источников, даст возможность генерировать преобразовательными блоками 10 и 11 максимально возможную реактивную мощность.
Если реактивная мощность нагрузки меньше оптимального для сети значения, то блоки 10 и 11 должны выполнять только задачу регулирования действующего значения напряжения нагрузки. В этом из равенства ![]() в (4) и
в (4) и ![]() в (6) получают амплитуды регулирующих тока
в (6) получают амплитуды регулирующих тока ![]() и напряжения
и напряжения ![]() . Загрузка блоков 10 и 11 реактивной мощностью в таком режиме фактически равна нулю, компенсируется только реактивная мощность силового трансформатора.
. Загрузка блоков 10 и 11 реактивной мощностью в таком режиме фактически равна нулю, компенсируется только реактивная мощность силового трансформатора.
В случае, когда реактивная мощность нагрузки сравнима с оптимальным для сети значением, то целесообразно сначала снижать генерацию реактивной мощности блоком 11, оставляя максимальной генерацию реактивной мощности блоком 10 (см. рис. 3б). Амплитуда управляющего напряжения получается из условия ![]() в (6). Амплитуда и фаза управляющего тока определяется уравнением (4). В этом случае силовой трансформатор будет загружен меньшей реактивной мощностью, что снизит потери в трансформаторе.
в (6). Амплитуда и фаза управляющего тока определяется уравнением (4). В этом случае силовой трансформатор будет загружен меньшей реактивной мощностью, что снизит потери в трансформаторе.
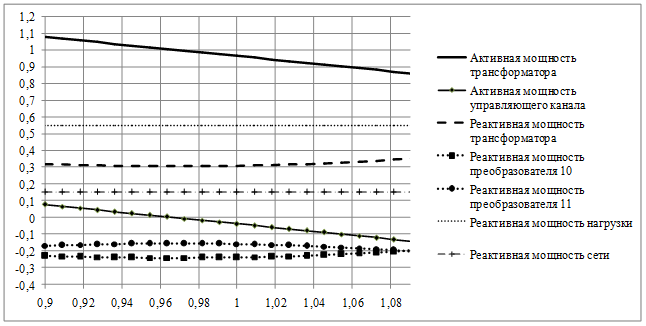
Рис. 4. Зависимости активной и реактивной мощности блоков устройства от напряжения сети
Поскольку границы между указанными областями достаточно условны, то при построении алгоритма управления, целесообразно воспользоваться нечеткой логикой [1]. Этот вопрос требует дальнейшей проработки.
Рассмотренная выше базовая математическая модель трансформатора с векторным управлением позволила только качественно описать его работу. Учет индуктивности рассеяния силового трансформатора можно выполнить следующим образом. Индуктивность рассеяния нагрузочной обмотки можно включить в индуктивное сопротивление эквивалентной нагрузки. Индуктивность рассеяния регулировочной обмотки можно отнести к эквивалентному фильтру. Таким образом, на схеме замещения (рис. 2) добавится только один дополнительный элемент ![]() , включенный последовательно с зависимым источником
, включенный последовательно с зависимым источником ![]() . Действующее значение напряжения на двух элементах
. Действующее значение напряжения на двух элементах ![]() будет определяться согласно записанным выше уравнениям. Напряжение на зависимом источнике
будет определяться согласно записанным выше уравнениям. Напряжение на зависимом источнике ![]() можно получить из баланса мощностей в виде
можно получить из баланса мощностей в виде
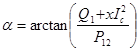 ,
, ![]() . (15)
. (15)
Однако такая модель по-прежнему не позволяет получить количественные результаты для используемых в настоящее время видов трансформаторов и активных преобразователей. Для этого необходима полная математическая модель рассматриваемого устройства, учитывающая потери в трансформаторах, фильтрах и активных преобразователях, а также моделирование устройства в пакете MATLAB Simulink с целью получения характеристик переходных процессов.
Выводы:
1) построена базовая математическая модель трансформатора с векторным управлением;
2) на основе математической модели показано, что трансформатор с векторным управлением позволяет осуществлять регулирование напряжения нагрузки и одновременно выполнять компенсацию реактивной мощности;
3) выбор оптимальных амплитуд и фаз управляющих тока и напряжения определяется отношением реактивной мощности нагрузки и реактивной мощности, которую целесообразно передать по сети;
4) в режиме максимальной загрузки генерация реактивной мощности осуществляется эффективно в каждом из преобразовательных блоков.
Рецензенты:
Ганджа С.А., д.т.н., профессор, заведующий кафедрой «Теоретические основы электротехники» ФГБОУ ВПО Южно-Уральский Государственный Университет (НИУ), г. Челябинск.
Воронин С.Г., д.т.н., профессор, заведующий кафедрой «Электромеханика и электромеханические системы» ФГБОУ ВПО Южно-Уральский Государственный Университет (НИУ), г. Челябинск.



