Введение
Строгий учет погрешностей численного решения естественнонаучных задач является одной из актуальных проблем компьютерного моделирования. Для корректного анализа сложных технических систем требуются математические модели, учитывающие неопределенность исходных данных. Эффективным средством учета неопределенности являются интервальные методы. Интервальный подход формировался вначале как метод автоматического контроля ошибок округления на ЭВМ, а затем и как средство учета влияния неопределенности в исходных данных на конечные результаты расчетов. Ценность интервальных вычислений заключается в том, что они дают возможность получения достоверного интервального решения, включающего не только диапазоны неопределенности входных параметров, но также и погрешности дискретизации задачи и компьютерных округлений [2].
В ходе интервальных вычислений результат гарантированно содержит множество всевозможных решений точечных задач, исходные значения которых содержатся в интервалах. Известно, что в некоторых случаях применение интервальных вычислений дает неудовлетворительные результаты из-за чрезмерной ширины получаемых интервалов [7].
Интервальный тип данных на множестве действительных чисел R реализуется на современных компьютерах представлением интервала двумя числами для его концов:
![]() ,
,
а множество всех интервалов обозначают I(R).
Арифметические операции определяются правилом [2, 7]:
![]() ,
,
где символу * соответствует одна из операций: ![]() .
.
Для ![]() и
и ![]() операции могут быть записаны в виде:
операции могут быть записаны в виде:
![]() ,
, ![]() ,
,
![]() ;
; ![]() ,
,
![]() ;
; ![]() ;
; ![]() .
.
Влияние погрешностей округления
Возникающая при вычислении интервальных границ погрешность включается в результирующий интервал с помощью направленных округлений: левая граница округляется к ![]() , правая к
, правая к ![]() . Режим округления процессора устанавливается с помощью функций, имеющихся в стандартных библиотеках многих систем программирования.
. Режим округления процессора устанавливается с помощью функций, имеющихся в стандартных библиотеках многих систем программирования.
Например, из свободного программного обеспечения, в среде Lazarus (компилятор Free Pascal Compiler) в модуле Math доступны функции:
o SetRoundMode(rmDown) – округление «вниз» (к ![]() ),
),
o SetRoundMode(rmUp) – округление «вверх» (к ![]() ).
).
В среде Orwell Dev-C++ (компилятор TDM GCC) в стандартной библиотеке fenv.h имеются аналогичные функции:
o fesetround (FE_DOWNWARD) – округление «вниз»,
o fesetround (FE_UPWARD) – округление «вверх».
Необходимо отметить, что многократное переключение режима округления процессора влечет за собой большие затраты: их использование в каждой интервальной операции увеличивает на порядок общее время счета. Поэтому, как правило, в модуле интервальных вычислений один раз устанавливается режим округления, например, «вниз». При этом операция сложения для интервала C = A + B может реализовываться следующим образом: c1 = a1 + b1; c2 = – (– a2 – b2). Аналогично преобразуются и другие интервальные операции.
В качестве примера учета направленного округления приведем результаты N-кратного (N = 109) суммирования вырожденного интервала: A = [10-9,10-9] с единицей. Очевидно, что при обычном округлении «к ближайшему» итоговая сумма должна быть равна двум, а ширина полученного интервала — нулю. Ниже для N, кратных 2*108, приведены результаты суммирования для базового типа с повышенной точностью (long double) с мантиссой 18 десятичных знаков (табл. 1) и для базового типа с двойной точностью (double) с мантиссой 15 знаков (табл. 2). Здесь a1, a2 — итоговые значения концов интервала, wa, wo — абсолютная и относительная ширина полученного интервала.
Таблица 1. Суммы вырожденных интервалов с базовым типом long double.
|
N*10-8 |
a1 |
a2 |
wa*1011 |
wo*1012 |
|
2 |
1.1999999999815 |
1.2000000000031 |
2.2 |
18 |
|
4 |
1.3999999999629 |
1.4000000000063 |
4.3 |
31 |
|
6 |
1.5999999999444 |
1.6000000000094 |
6.5 |
41 |
|
8 |
1.7999999999259 |
1.8000000000126 |
8.7 |
48 |
|
10 |
1.9999999999073 |
2.0000000000157 |
11 |
54 |
Таблица 2. Суммы вырожденных интервалов с базовым типом double.
|
N*10-8 |
a1 |
a2 |
wa*108 |
wo*108 |
|
2 |
1.1999999721 |
1.2000000165 |
4.4 |
3.7 |
|
4 |
1.3999999443 |
1.4000000331 |
8.9 |
6.3 |
|
6 |
1.5999999164 |
1.6000000496 |
13 |
8.3 |
|
8 |
1.7999998886 |
1.8000000662 |
18 |
9.9 |
|
10 |
1.9999998607 |
2.0000000827 |
22 |
11 |
Из приведенного примера видно, что использование типа long double приводит к ширине результирующего интервала в среднем на два-три порядка меньше, чем в аналогичных расчетах с типом double. В то же время применение типа double сокращает время счета примерно в полтора-два раза по сравнению с типом long double.
Учет погрешности дискретизации численного метода
В методе граничных элементов, который используется в данной работе, применяется «двойной пересчет» на двух граничных сетках с шагами h1 и h2 = h1/2. Затем по результатам двух решений на основании формулы Рунге [3], оценивается погрешность численного метода, которая включается в результирующий интервал.
Математическая модель электрического поля
Рассмотрим задачу расчета электрического поля в простейшей электрохимической системе с плоскими параллельными электродами. Область решения в трехмерном случае имеет вид: ![]()
![]()
![]()
![]() .
.
Известно, что потенциал u(p) стационарного электрического поля при отсутствии точечных источников удовлетворяет уравнению эллиптического типа:
![]() ;
; ![]() ,
,
где ![]() — удельная электропроводность среды, См/м,
— удельная электропроводность среды, См/м,
При ![]() потенциал u(p) удовлетворяет уравнению Лапласа:
потенциал u(p) удовлетворяет уравнению Лапласа:
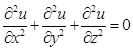 . (1)
. (1)
Границам-изоляторам (Si) соответствуют краевые условия второго рода:
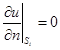 , (2)
, (2)
где n — вектор внешней нормали к границе.
На границах электролита с анодами (Sa) и катодами (Sс), в случае линейной зависимости плотности тока от разности потенциалов на обкладках двойного слоя, выполняются краевые условия третьего рода:
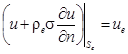 ,
, ![]() , (3)
, (3)
где
индекс «e» принимает значение «a» для анода и «c» — для катода;
ρa, ρс — удельные сопротивления на границе электрод/электролит (Ом.м2);
ua, uс — потенциалы электродов (В), разность которых равна приложенному напряжению от внешнего источника тока.
Для системы с плоскими параллельными электродами решение задачи (1) – (3) в одномерной постановке, которое несложно получить аналитически в виде формулы, должно в определенном смысле совпадать с решениями, полученными численными методами, в двумерной (прямоугольник) и трехмерной (параллелепипед) областях. В частности, представляет интерес анализ и сравнение результатов решения подобных задач с интервальными исходными данными для областей различной размерности.
Одномерная задача
Сформулируем задачу (1) – (3) для одномерного случая (u = u(x)):
![]() ;
; ![]() , (4)
, (4)
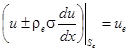 ,
, ![]() . (5)
. (5)
Общее решение уравнения (4) представимо в виде
![]() , (6)
, (6)
где A и B — произвольные константы.
Удовлетворяя решением (6) граничным условиям (5), легко получить систему двух уравнений для определения A и B, подставив которые в (6) будем иметь выражение для потенциала u(x) в любой точке из отрезка [0, Lx]:
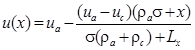 . (7)
. (7)
Из соотношения (7) определим значения потенциала в электролите на границах анода (x = 0) и катода (x = Lx):
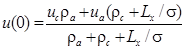 , (8)
, (8)
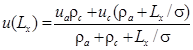 . (9)
. (9)
Далее соотношения (7) – (9) используются в качестве тестовых решений одномерной задачи с интервальными исходными данными.
Двумерная задача
Для решения задачи (1) – (3) в двумерной постановке предлагается метод граничных элементов, который без принципиальных осложнений можно использовать в областях с границей произвольной конфигурации [1, 5, 10], а также в трехмерных задачах [6, 8, 9]. Для построения граничного интегрального уравнения воспользуемся интегральной формулой Грина, которая с учетом уравнения (1), для точек p и q, лежащих на границе S, примет вид:
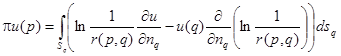 , (10)
, (10)
где ![]() — расстояние между точками p и q.
— расстояние между точками p и q.
Из формулы (10) с учетом граничных условий (2), (3) после некоторых преобразований будем иметь интегральное уравнение относительно неизвестной функции u
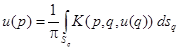 , (11)
, (11)
в котором ядро K(p, q, u(q)) определяется следующими соотношениями (аргументы p и q для краткости опущены):
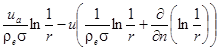 , если
, если ![]() ;
; ![]() ;
;
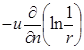 , если
, если ![]() .
.
Алгоритм решения уравнения (11) может быть построен на основе метода конечных сумм, путем сведения его к системе линейных алгебраических уравнений. Так как в реальных задачах рассматриваемого типа граничные условия (3), как правило, нелинейны, то более универсальным подходом представляется применение итерационной процедуры [5]:
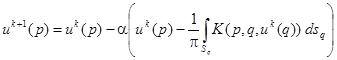 , (12)
, (12)
где k — номер итерации; α — итерационный параметр, выбираемый из условия сходимости процесса.
Изложенный алгоритм — метод граничных элементов в сочетании с итерационной процедурой (12) — неоднократно применялся при решении аналогичных задач в областях более сложной геометрии, в том числе в трехмерных задачах с нелинейными граничными условиями, но без учета интервальных исходных данных, погрешностей дискретизации задачи и погрешностей округления.
Необходимо отметить, что количество итераций в процедуре (12) зависит от сложности геометрии области, размерности задачи и требуемой точности результатов и может оказаться достаточно большим. В этом случае, вследствие накопления погрешностей округления в задачах с интервальными исходными данными, ширина результирующего интервала может превзойти допустимые пределы.
В работе используется методика, изложенная в [4], которая предполагает на первом этапе решения задачи применение традиционных численных методов на множестве действительных чисел, после чего, на заключительном этапе, применение интервальных вычислений.
Вычислительный эксперимент
Изложенный метод апробирован в расчетах электрического поля при следующих значениях основных параметров на первом «доинтервальном» этапе: Lx = Ly = 1.0 м; ρa = ρc = 0.7 Ом*м2; ua = 5 В; uc = 2 В; σ = 12 См/м; число граничных элементов по сторонам квадрата: Nx = Ny = 100; значение итерационного параметра в процедуре (12): α = 0.5; обход границы S в интегральном уравнении — от 0 до Lx, далее по периметру квадрата против часовой стрелки.
Сравнение численных решений двумерной и одномерной задач на множестве действительных чисел (зависимости 1 на рис. 1) показало: их отличие в произвольных точках p границы S не превышает 2×10-5 для функции u(p) и 3×10-5 для функции j(p), что в масштабе рисунка неразличимо. Интервальные решения (зависимости 2 и 3) построены для различных интервальных исходных данных, значения которых указаны в подрисуночной подписи.
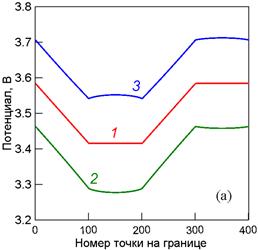
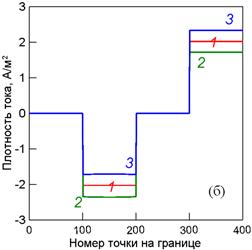
Рис. 1. Распределение потенциала (а) и плотности тока (б) в электролите по границе области: 1 – при точных исходных данных; 2, 3 – нижняя и верхняя границы интервальных решений при ua = [4.95, 5.05], uс = [1.95, 2.05]; ρa = ρс = [0.68, 0.72]; σ = [11.5, 12.5].
Таим образом, интервальные решения на рис. 1 включают погрешности исходных данных, погрешности дискретизации численного метода и погрешности компьютерных округлений. При разработке программного продукта использовалась среда Orwell Dev-C++ с компилятором TDM GCC, распространяемая по лицензии GPL.
Выводы
На основе метода граничных элементов построен алгоритм численного решения двумерной краевой задачи для потенциала электрического поля в электрохимической системе c плоскими параллельными электродами. Проведены расчеты электрического поля с интервальными входными параметрами в одно- и двумерной постановках, представлены результаты решений. Направление дальнейших исследований предполагает переход к более общим трехмерным математическим моделям с интервальными исходными параметрами, с учетом неодносвязности области, криволинейности границ и нелинейности краевых условий.
Рецензенты:
Асадуллин Р. М., д.ф.-м.н., профессор кафедры программирования и вычислительной математики ФГБОУ ВПО «Башкирский государственный педагогический университет имени М. Акмуллы», г. Уфа;
Бронштейн Е. М., д.ф.-м.н., профессор кафедры вычислительной математики и кибернетики ФГБОУ ВПО «Уфимский государственный авиационный технический университет», г. Уфа.



