Введение
Временные и фазовые искажения сигналов информации (джиттер) в каналах записи-воспроизведения (КЗВ) аппаратуры цифровой магнитной записи (накопители на магнитных дисках и лентах) в значительной степени определяют надежность сохранения информации. Поэтому математическое описание джиттера, который вызван совокупным действием многих факторов, носящих в общем случае стохастический характер, имеет важное значение для проектирования конструкции электромеханических узлов накопителей, их каналов записи-воспроизведения, а также контроля [1,2]. Предлагаемый подход к построению модели временных искажений базируется на обработке экспериментальных данных о временных искажениях сигналов в КЗВ, возможность получения которых обеспечивается оригинальной контрольно-измерительной аппаратурой [3].
Будем считать исследуемым временным параметром сигнала в канале НМД его мгновенный период – временной интервал между передними (задними) фронтами информационных импульсов (например, с выхода пикового детектора канала воспроизведения). Мгновенное значение временного интервала определяется:
- кодовой комбинацией, сформировавшей сигналограмму на соответствующем участке носителя;
- амплитудно-частотной характеристикой КЗВ;
- нестабильностью параметров КЗВ (непостоянство линейной скорости носителя и величины рабочего зазора магнитной головки);
- шумами носителя и электронной части КЗВ.
Для того чтобы обеспечить раздельный анализ искажений, вызванных межсимвольной интерференцией и другими дестабилизирующими факторами, измерения временных интервалов проводятся при воспроизведении предварительно записанной на дорожке периодической кодовой последовательности, которая должна формировать все временные интервалы, соответствующие используемому методу канального кодирования, причем желательно записывать их «тяжелую» комбинацию.
Джиттер – сложный процесс, состоящий из множества компонент, которые определяются особенностями работы устройства чтения/записи (биение головки, центробежные силы при вращении дисков, температурный режим эксплуатации устройства и т.п.), но при этом джиттер условно можно разделить на 2 части: 1 – квази детерминированный джиттер; 2 – чисто случайный [4].
Традиционно задачи построения моделей временных рядов состоят из следующих этапов:
- выделение квази-детерминированной компоненты в виде тренда и интерпретация его как низкочастотной составляющей;
- приведение процесса к стационарному;
- построение линейной модели стационарного процесса.
Для описания квази-детерминированной компоненты обычно используется аналитический подход, основанный на некотором эвристическом предположении о его характере. Например, в [5] для аппроксимации тренда используются полиномы Чебышева. В любом случае, выделение квази-детерминированных компонент связано с основанным на опыте исследователя выбором вида уравнения, размерности полиномов и оценки их значений для каждой реализации, что является достаточно ресурсоемким процессом.
В отличие от традиционного подхода, в настоящей работе предлагается применить для выделения квази-детерминированных и чисто случайных компонент джиттера алгоритм «Гусеница» [6, 7], суть которого в преобразовании одномерного ряда в многомерный с помощью однопараметрической сдвиговой процедуры (отсюда и название «Гусеница») и исследовании полученной многомерной траектории с помощью анализа главных компонент (сингулярного разложения) с последующим восстановлением ряда по выбранным главным компонентам. Результатом применения алгоритма является разложение исходного временного ряда на простые компоненты: медленные тренды и другие периодические или колебательные составляющие, а также чисто шумовые компоненты.
Формирование исходных данных
Основой для построения модели квази-детерминированной компоненты джиттера служит временной ряд, описывающий поведение мгновенного периода информационного сигнала в канале КЗВ.
Последовательность измерений синхронизируется таким образом, чтобы измерялись временные интервалы, соответствующие одноименным позициям воспроизводимой кодовой последовательности.
В связи с высокой скоростью работы накопителя и относительно низкой производительностью (10^7 измерений/сек) при высокой разрешающей способности (0.82 нс) измерителя получены данные не о каждом мгновенном периоде (рисунок 1).
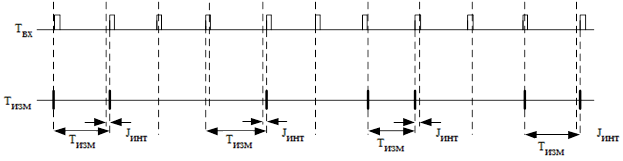
Рисунок 1. Измерение не смежных временных интервалов.
Построение модели джиттера с использованием алгоритма «Гусеница»
Для построения модели квази-детерминированного джиттера в каналах чтения/записи НМД автором предложен следующий алгоритм:
Шаг 1. Вычисление интервального джиттера
На рисунке 2 представлена измеренная реализация мгновенных периодов (![]() ) информационного сигнала КЗВ, выраженная в квантах измерителя, по оси абсцисс указан номер измерения, по оси ординат длительность мгновенного периода. Периодичность измерений периодов – 2760.
) информационного сигнала КЗВ, выраженная в квантах измерителя, по оси абсцисс указан номер измерения, по оси ординат длительность мгновенного периода. Периодичность измерений периодов – 2760.
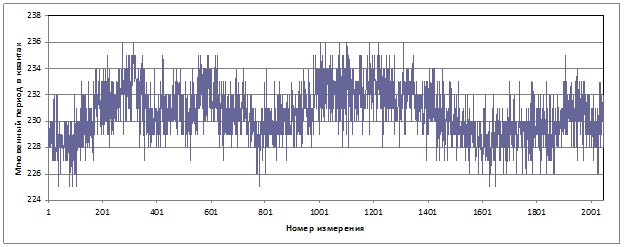
Рисунок 2. Исходные данные
Вычисление интервального джиттера выполняется по формуле:
![]() ((1)
((1)
Временной ряд, определяемый как отклонение мгновенного периода от его среднего значения, полученный по формуле (2), является исходными данными для гусеницы.
![]() ((2)
((2)
Как было показано в работе [8], восстановление информации о квази-детерминированной компоненте джиттера на пропущенных интервалах предпочтительнее выполнять после выделения квази-детерминированной компоненты «Гусеницей».
Шаг 2. Восстановление квази-детерминированной компоненты джиттера с использованием «Гусеницы»
Алгоритм метода «Гусеница» можно разделить на несколько этапов.
1.1. Вложение. Выполняется преобразование исходного ряда в последовательность ![]() -мерных векторов, число которых равно
-мерных векторов, число которых равно ![]() :
:
![]() ,
, ![]() , где N – длина временного ряда, L – длина окна «Гусеницы»
, где N – длина временного ряда, L – длина окна «Гусеницы»
2. Сингулярное разложение. Результатом этого шага является сингулярное разложение траекторной матрицы ряда:
![]()
![]() , где
, где ![]() собственные числа матрицы
собственные числа матрицы ![]() , взятые в порядке убывания
, взятые в порядке убывания ![]() ;
; ![]() – отронормированная система собственных векторов матрицы
– отронормированная система собственных векторов матрицы ![]() , соответствующих собственным числам
, соответствующих собственным числам ![]() .
.
В результате преобразований получим разложение траекторной матрицы:
![]() , где
, где ![]()
3. Группировка. Выбрав интересующие нас компоненты, выполним процедуру группировки. Для группировки и восстановления ряда рекомендуется брать первые 2–3 компоненты, т.к. остальные представляют собой реализацию «белого шума».
4. Диагональное усреднение. На последнем шаге каждая матрица сгруппированного разложения переводится в новый ряд длины ![]() по формуле
по формуле
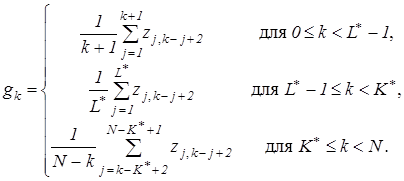
где ![]()
Таким образом, результатом применения метода является разложение временного ряда на простые компоненты: медленные тренды и периодические или колебательные составляющие, а также шумовые компоненты.
Полученное разложение служит основой прогнозирования как самого ряда, так и его отдельных составляющих.
Анализируя поведение компонент, полученных при различной длине окна гусеницы, было определено, что данный временной ряд удовлетворительно описывает реализация «Гусеницы» при длине окна ![]() . В таблице 1 приведены удельные веса первых 4 компонент «Гусеницы»
. В таблице 1 приведены удельные веса первых 4 компонент «Гусеницы»
Таблица 1. Удельный вес компонент «Гусеницы»
|
Номер компоненты «Гусеницы» |
Удельный вес компоненты, % |
|
1 |
34,226 |
|
2 |
6,129 |
|
3 |
2,230 |
|
4 |
1,051 |
\ На рисунке 3 показано, как изменяется квази-детерминированная компонента интервального джиттера в зависимости от числа выбранных компонент: Komp1 – одна компонента; Komp2 – две компоненты; Komp3 – компоненты; Komp4 – четыре компоненты.
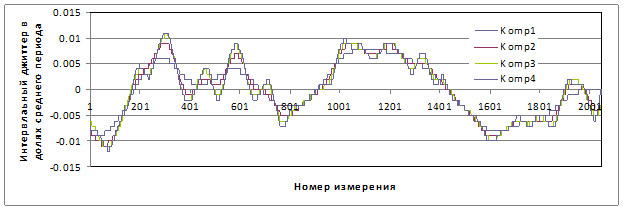
Рисунок 3. Реализации квази-детерминированной компоненты интервального джиттера
Анализ остатка после обработки сигнала «Гусеницей»
Оставшаяся часть ряда, которая была отброшена на этапе группировки существенных компонент «Гусеницы», подчиняется закону нормального распределения, что подтверждается критерием Колмогорова – Смирнова и гистограммой распределения.
Шаг 3. Интерполяция значений квази-детерминированного джиттера на пропущенные интервалы
Для восстановления информации на пропущенных временных интервалах применим механизм интерполяции 0-го порядка, тогда:
![]() , где
, где ![]() - количество пропущенных интервалов измерений;
- количество пропущенных интервалов измерений;
![]() - джиттер
- джиттер ![]() -го измеренного интервала.
-го измеренного интервала.
Полученная квази-детерминированная компонента интервального джиттера представляет самостоятельный интерес для конструкторов и технологов, поскольку несет информацию о влиянии на информационный сигнал электро-механических узлов НМД.
Для оценки поведения селектора информации необходимо вычислить квази-детерминированную компоненту фазового джиттера, который определим как отклонение временного положения информационного сигнала от его положения на идеальной шкале синхросигнала.
В существующих системах, для выделения данных из информационного сигнала применяется его стробирование синхросигналом, формируемым инерциальной системой фазовой автоподстройки частоты (ФАПЧ), которая позволяет убрать из поступающего сигнала низко-частотные компоненты, которые могут привести к ошибке из-за их накопления [9].
Шаг 4. Переход от интервального джиттера к фазовому
Для перехода к фазовому джиттеру можно воспользоваться следующей формулой:
![]() (4)
(4)
На рисунке 4 представлен график поведения квази-детерминированной компоненты джиттера в каналах чтения записи НМД
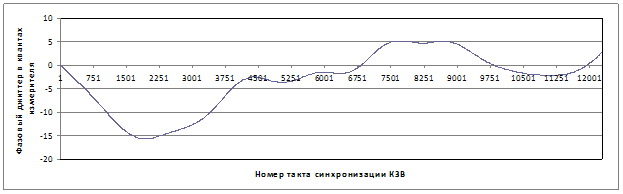
Рисунок 4. График квази-детерминированной фазовой компоненты джиттера
Рассмотрим возможность коррекции полученного фазового джиттера системой инерциального ФАПЧ, для этого воспользуемся моделью простейшего ФАПЧ, описанной в [10], и определим его следующие параметры:
- коэффициент фазового детектора
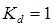 ;
; - коэффициент генератора управляемого напряжением
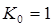 ;
; - резонансная частота контура
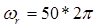 ;
; - демпинг фактор
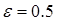 ;
; - частота дискретизации
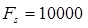 Гц.
Гц.
Пропустив квази-детерминированную компоненту «Гусеницы» через фильтр, мы получим ошибку, которую фильтр не убрал из исходного сигнала.
На рисунке 5 представлены гистограммы распределения ошибки ФАПЧ и общей ошибки
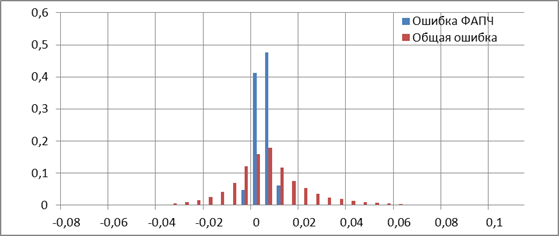
Рисунок 5. Гистограмма распределения ошибки
Область допустимых значений фазовых искажений в накопителе (нормирования) определяется, исходя из условия обеспечения требуемой достоверности воспроизведения записанной периодической байтовой последовательности, соответствующей «тяжелому» коду, при котором наибольшая межсимвольная интерференция.
Заключение
Метод «Гусеница» позволяет выделять квази детерминированную составляющую джиттера при отсутствии априорной информации о его структуре и различной полноте измерений (пропусков в реализации сигнала) и оценивать величину квази-детерминированной компоненты на каждом тактовом интервале, вне зависимости от того, проводилось ли его измерение.
Рецензенты:
Цыпин Б.В., д.т.н., профессор кафедры ИИТ, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Пензенский государственный университет», г. Пенза.
Чулков В.А., д.т.н., профессор, декан факультета заочного обучения Пензенского государственного технологического университета, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Пензенский государственный технологический университет», г. Пенза.



