Задача оптимального (и, в частности, экстремального) управления на минимум ресурсов нелинейными динамическими объектами представляет сложную, до конца не решённую проблему. Общей методики для решения нелинейных оптимальных задач не существует ввиду их большого разнообразия. В качестве основного метода исследования оптимального управления используется принцип максимума Понтрягина, учитывающий ограничения на переменные системы и поэтому применяемый для решения практических задач, и условия общности положения (УОП) для нелинейных объектов в расширенном пространстве координат [3,4,5].
Нестационарность нелинейных объектов с экстремальной статической характеристикой проявляется в дрейфе статической характеристики, который может быть вертикальным или горизонтальным, и получается при различном вхождении времени в уравнения движения объекта – аддитивном, мультипликативном и смешанном. Под аддитивным вхождением времени понимается случай, когда в уравнениях движения время суммируется с координатами объекта, под мультипликативным – когда время умножается на координаты объекта. При смешанном вхождении в уравнения движения переменная 
суммируется и умножается на координаты объекта.
В данной статье исследуются нестационарные нелинейные объекты при вертикальном дрейфе статической характеристики с аддитивным вхождением времени в математическое описание объекта управления (ОУ).
ОУ представлен в виде структуры образованной последовательным соединением линейного динамического звена и нелинейного динамического звена с экстремальной статической характеристикой, и эта структура может быть описана системой дифференциальных уравнений нелинейных по координатам 
, но линейных по управлениям 
где 
– функциональная матрица - столбец с элементами 
, 
; 
- функциональная матрица – столбец с элементами 
, (функции , , , непрерывны и достаточное число раз непрерывно дифференцируемы по ); – скалярная функция.
Необходимо найти допустимое управление , 
, доставляющее минимум интегральному критерию
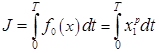. (1)
где T – время движения от начальной до конечной точки заранее не задано.
Как показано в [6], для исследования нестационарных задач используется рекуррентное соотношение:
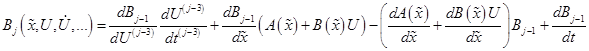, (2)
где 
, 
, 
.
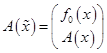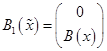Из векторов 
, 
, составляется матрица 
. Если определитель матрицы 
, то из выражения 
определяется множество особых управлений в функции фазовых координат и параметров системы.
Дифференциальные уравнения связи, характеризующие ОУ, имеют вид:
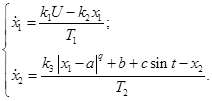(3)
Статическая характеристика объекта (3) выражается уравнением 
, а экстремум статической характеристики имеет координаты 
.
Модель (3) в общем случае является неаналитической функцией, за исключением случаев четных показателей q, например, при 
получается аналитическое уравнение квадратичной статической характеристики. Вместе с тем относительно неаналитической модели (3) предполагается, что в подпространствах входной координаты нелинейного звена 
и 
известны соответствующие аналитические функции, тогда
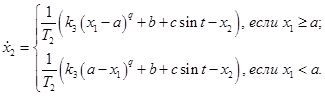(4)
Рассмотрим подпространство . В задаче на минимум функционала (2) получаем особое управление
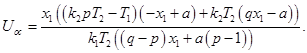(5)
Система (3) под особым управлением (5) примет вид:
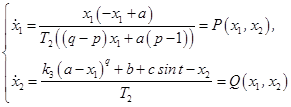(6)
Состояниями равновесия (особыми точками) системы (6) являются точка экстремума статической характеристики 
и точка с координатами 
. Применяя качественную теорию дифференциальных уравнений [1,2], найдём в окрестности особых точек параметры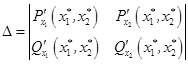 
, 
, а также корни характеристического уравнения 
:
1) в окрестности точки параметры 
, 
, корни характеристического уравнения 
, 
;
2) в окрестности точки параметры 
, 
, корни характеристического уравнения , 
.
Сделаем некоторые выводы о состояниях равновесия системы (6). В окрестности особой точки при 
, корни характеристического уравнения действительные, разных знаков, особая точка является седлом. При 
особая точка не является состоянием равновесия. При 
(критерий быстродействия) детерминант матрицы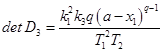 
, из приравнивания нулю которого определяется уравнение особой траектории 
.
В окрестности особой точки при 
, корни характеристического уравнения действительные, одинаковых знаков, особая точка является устойчивым состоянием равновесия – узлом. При 
, корни характеристического уравнения действительные, разных знаков, особая точка является седлом.
При 
и 
система (6) имеет единственное состояние равновесия . В этом случае параметры принимают следующий вид: , , корни характеристического уравнения 
, 
при (в этом случае особая точка является седлом), и 
при 
(в этом случае особая точка является узлом).
При и детерминант матрицы 
равен постоянному, отличному от нуля числу. В этом случае особых режимов не возникает, управление однозначно определяется принципом максимума 
и является релейным, с максимально допустимыми амплитудами на интервалах между переключениями.
Идентичные результаты получаются при анализе подпространства . Результаты моделирования для параметров 
, 
, 
, 
, 
, , 
, 
представлены на рисунке 1; для параметров 
, 
, , 
, , 
, , представлены на рисунке 2.
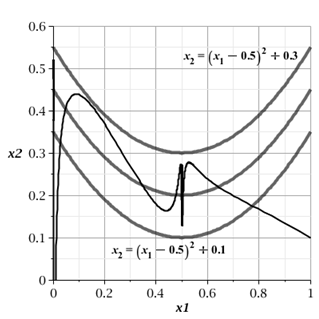
Рисунок 1. Фазовые траектории системы (6), два состояния равновесия – точки 
, 
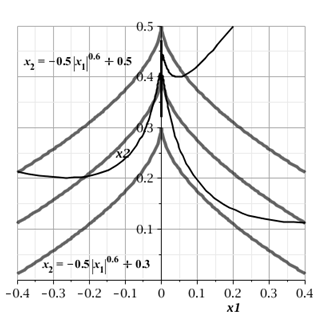
Рисунок 2. Фазовые траектории системы (6), одно состояние равновесия – точка 
Вывод
Выбирая величину параметра 
в интегральном функционале (2), можно добиться асимптотической устойчивости точки экстремума статической характеристики системы (3) под действием особого управления (5). Из графиков переходных процессов видно, что под особым управлением траектории системы устойчивы, т.е. подтверждаются результаты качественного исследования, причем происходит отслеживание дрейфующих точек экстремума.
Рецензенты:
Присмотров Н.И., д.т.н., профессор кафедры ЭПиАПУ, ФГБОУ ВПО «Вятский государственный университет», г. Киров.
Частиков А.В., д.т.н., профессор, декан факультета прикладной математики и телекоммуникаций, ФГБОУ ВПО «Вятский государственный университет», г. Киров.