Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Введение

Задача идентификационного управления [1] возникает в условиях, когда математическая модель объекта управления неизвестна. Такие задачи встречаются при управлении сложными техническими объектами, в том числе при управлении мобильными роботами. Задача синтеза идентификационного управления состоит из двух задач: задачи идентификации математической модели объекта и задачи синтеза системы управления для полученной модели. Настоящая работа посвящена решению задачи синтеза идентификационного управления методом сетевого оператора [2-10].

Метод сетевого оператора позволяет получать математические выражения в форме целочисленной матрицы. В работе используем метод сетевого оператора для решения обоих задач. В решении задачи синтеза используем математическую модель, полученную при решении задачи идентификации.

В качестве практического примера метод синтеза идентификационного управления применяем для технического объекта, мобильного гусеничного робота Lego NXT.

1. Задача синтеза идентификационного управления

Задано множество экспериментальных данных:

, (1)

где – вектор входного управления в момент , – вектор выходных переменных в момент , – число точек наблюдения, , .

Задана размерность модели объекта управления.

Задана функция определения вектора наблюдения по вектору состояния объекта

, (2)

где .

Задано множество начальных условий для объекта

. (3)

Задана цель управления

, (4)

где – время окончания процесса управления определяется выполнением условия (4).

Задан критерий качества

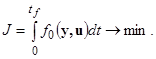(5)

Необходимо найти решение в виде

(6)

где – вектор параметров для задачи синтеза, .

Для решения задачи первоначально находим математическую модель объекта управления в виде системы обыкновенных дифференциальных уравнений

(7)

где – вектор искомых параметров, который вводится в правые части дифференциальных уравнений для расширения пространства поиска, , размерность определяется исследователем по сложности задачи и объекта,

.

Решение в точках , , при , должно совпадать с результатами эксперимента. Для оценки качества найденного решения используем следующие функционалы:

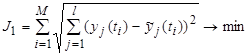, (8)

(9)

Для решения задачи идентификации (1), (2), (7)-(9) используем метод сетевого оператора [1-7]. В результате решения задачи идентификации получаем систему обыкновенных дифференциальных уравнений (7).

На втором этапе решаем задачу синтеза системы управления (3)-(6) для математической модели (7), полученной на первом этапе. При решении задачи также используем метод сетевого оператора. Подробно метод сетевого оператора описан в работах [2-10].

2. Практический пример

В качестве эксперимента было рассмотрено решение задачи синтеза идентификационного управления для робота LEGO NXT [11] (рис. 1).

Рис.1. Робот LEGO NXT.

Робот имеет 4 колеса с радиусом см. Расстояния, пройденные колесами робота, рассчитываются по формулам

,

где , – расстояния, пройденные, соответственно, левой и правой парами колес, – углы вращения колес в радианах.

В эксперименте для получения исходных данных управление роботом осуществлялось с помощью функции времени

,

где .

Было проведено несколько экспериментов по 21 точке. Вычислялись средние значения по всем экспериментам. Экспериментальные данные приведены в табл.1 .

Таб. 1. Экспериментальные данные

При решении задачи идентификации было выбрано следующее базисное решение

,

,

.

Базисные значения параметров: , , . В результате была получена следующая матрица сетевого оператора:

В матрице сетевого оператора номера унарных и бинарных операций соответствуют функциям, приведенным в приложениях [2]. В результате из матрицы сетевого оператора получаем следующее решение:

, (10)

(11)

, (12)

(13)

где

, , , , ,

Параметры генетического алгоритма: размерность популяции – 256, количество скрещиваемых пар в поколении – 64, количество поколений – 256, число поколений между эпохами – 30, длина структурной части хромосомы – 8, число постоянных параметров – 6, количество бит под целую часть параметра – 2, количество бит под дробную часть параметра – 6, вероятность мутации – 0,7, шаг интегрирования – 0.001, размерность матрицы сетевого оператора – 22 х 22. Расчет проводился на программном комплексе NOP4C-I для идентификации систем управления методом сетевого оператора, разработанном на кафедре кибернетики и мехатроники РУДН [7]. Время расчета составляло 2,2 часа на ЭВМ с частотой процессора 2,2 ГГц, тип процессора Intel Core i5.

Результаты моделирования полученной модели системы управления представлены на рис. 5 - 7. Кружками отмечены экспериментальные данные из таблицы 1.

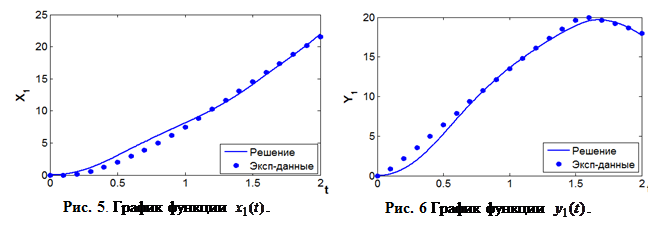
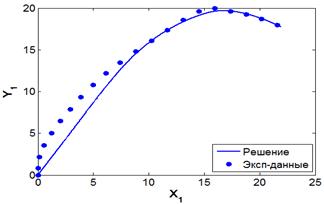
Рис. 7. График фазовой траектории .

Как видно из графиков, решения, полученные в результате идентификации модели, соответствуют исходным данным.

На втором этапе осуществляем синтез системы управления мобильным роботом Lego NXT с учетом полученной на этапе идентификации модели. Для решения задачи синтеза также применяем метод сетевого оператора.

При синтезе рассматривалась следующая задача. Задана траектория движения робота в виде упорядоченного множества точек

. (14)

Для модели (10)-(13) необходимо найти управление в форме

, (15)

которое минимизирует отклонение траектории робота от заданной траектории (14) по значениям критериев (8)-(9) при начальных условиях , . Управление ограничено значениями

Заданная траектория огибает препятствие и приведена на рис. 8.

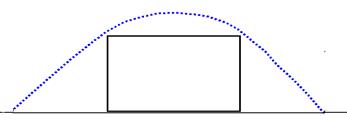
Рис. 8. Заданная траектория

Выбираем базисное решение в виде:

,

где , .

При решении использовали следующие параметры генетического алгоритма: размерность популяции – 256, количество скрещиваемых пар в поколении – 64, количество поколений – 256, число поколений между эпохами – 30, длина структурной части хромосомы – 8, число постоянных параметров – 6, количество бит под целую часть параметра – 4, количество бит под дробную часть параметра – 4, вероятность мутации – 0,7, шаг интегрирования – 0.001, размерность матрицы сетевого оператора – 16х16. Расчет проводился на программном комплексе NOP4C-S для идентификации систем управления методом сетевого оператора, разработанном на кафедре кибернетики и мехатроники РУДН [8]. Время расчета составляло 2 часа на ЭВМ с частотой процессора 2,2 ГГц, тип процессора Intel Core i5.

В результате было получена следующая матрица сетевого оператора:

.

Данная матрица соответствует следующему математическому выражению:

где

На рис.9 – 12 приведены результаты моделирования полученной системы управления.

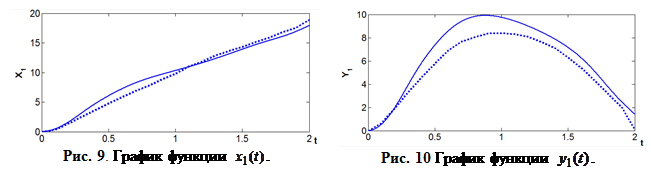
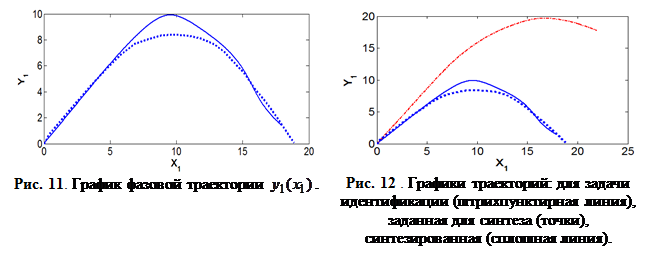
Для сравнения на рис. 12 приведена траектория движения робота, использованная при решении задачи идентификации. Как видно из графиков, полученная при идентификации математическая модель позволяет синтезировать систему управления роботом LEGO NXT, которая обеспечивает качественное движение по заданной траектории.

3. Заключение

В результате применения метода сетевого оператора была решена задача синтеза идентификационного управления мобильным роботом LEGO NXT. Результаты экспериментов показали удовлетворительное качество решения задач идентификации и синтеза управления.

Работа выполнена по теме грантов РФФИ №13-08-00523-а «Исследование и разработка численного метода идентификации моделей интеллектуальных систем управления»,
№ 14-08-00008-а «Исследование методов синтеза систем управления в условиях неопределенности».

Рецензенты:

Забудский Е.И., д.т.н., профессор, ФГБОУ ВПО «Московский агроинженерный университет им. В.П. Горячкина», г. Москва.

Юрков Н.К., д.т.н., профессор, ФГБОУ ВПО «Пензенский государственный университет», г. Пенза.