Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Введение

С физиологической точки зрения наиболее значимым является подразделение спортивных нагрузок на аэробные (циклические виды спорта) и анаэробные (скоростно-силовые и сложно-координационные виды спорта). При подготовке спортсменов различной специализации могут преобладать или анаэробные (борьба) или аэробные нагрузки (лыжные гонки), которые могут оказывать диаметрально противоположные влияния на функциональное состояние систем транспорта кислорода и на систему иммунобиологического надзора. В связи с этим весьма актуальной является проблема отбора для занятий конкретным видом спорта [4]. В настоящей работе сделана попытка на основе современных методов математического моделирования создать научно обоснованный способ классификации принадлежности конкретного спортсмена к определенной профессиональной группе, что может послужить основой для системы профессионального отбора для занятий конкретным видом спорта.

Материал и методы исследования

Исследования проведены на здоровых мужчинах-добровольцах, профессионально занимающихся лыжным спортом, плаванием, борьбой (самбо, дзюдо) и боксом и достигших определенной квалификации в этих видах деятельности. Исследовались показатели периферической крови и иммунного статуса организма [2]. Статистическая обработка результатов наблюдений за спортсменами проводилась с использованием лицензионного пакета программ прикладной статистики SPSS 17.0 [3]. У каждого спортсмена измерялись и вычислялись 65 показателей. Таким образом, можно сказать, что каждый спортсмен есть точка в 65-мерном фазовом (фиктивном) пространстве. Целями статистической обработки являлось выявление минимально необходимого количества показателей (переменных, изучаемых у спортсменов), позволяющих отнести спортсмена к той или иной специализации, и выявление минимально необходимого количества показателей, наиболее сильно влияющих на их специализацию. Такой подход позволяет оптимальным образом организовать профессиональную подготовку и может быть применен с целью отбора наиболее перспективных спортсменов [1].

Результаты исследования и их обсуждение

На первом этапе выполнялся факторный анализ всех переменных без учета специализации и квалификации спортсменов с целью определения возможности уменьшения размерности пространства переменных. Была сделана попытка уменьшить размерность пространства переменных в два раза. Было задано сформировать новое пространство с размерностью тридцать.

На рис. 1 приведены собственные значения, из которых видно, что нет необходимости увеличивать размерность пространства переменных более 30-ти.

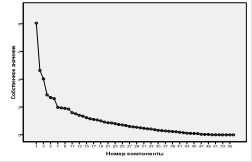
Рис. 1 График собственных значений пространства исследуемых переменных.

Факторный анализ показал также, что 30 компонент обеспечивают более 92 % объясненной дисперсии, что также вполне достаточно для анализа распределения спортсменов по специализациям. При выполнении факторного анализа вращение было задано по типу «варимакс с нормализацией Кайзера», которое сошлось за 34 итерации. Анализ матрицы повернутых компонент подтвердил правильность выбранной стратегии при выборе пространства переменных. Только первый фактор включил в себя 7 переменных, связанных в основном показателями системы красной крови. Эти переменные приведены в таблице 1.

Таблица 1

Переменные, входящие в первый фактор

Первый фактор (7 переменных) объясняет более 12 % дисперсии, и факторная нагрузка оказалась очень велика. Полученный результат подтверждает данные литературы об основном вкладе систем транспорта кислорода и, в частности, периферического отдела эритрона в специализацию, квалификацию и достижение высокого спортивного результата. Остальные факторы включают от одной до трех переменных, причем факторов с тремя переменными всего три, что подтверждает правильность выбранной стратегии анализа.

На втором этапе выполнялся дискриминантный анализ раздельно по спортивной специализации (лыжники, пловцы, борцы, боксеры). Дискриминантный анализ использовал пошаговый метод и выполнялся в двух вариантах: для всех 65-ти переменных и для переменных, выбранных на основании факторного анализа. Так как количество специализаций четыре, то дискриминантных функций достаточно использовать только три. В таблице 2 приведены собственные значения, процент объясненной дисперсии и коэффициент канонической корреляции для каждой из них.

Таблица 2

Собственные значения, процент объясненной дисперсии и коэффициент канонической корреляции для дискриминантных функций

Из таблицы 2 видно, что коэффициенты канонической корреляции достаточно велики, что позволяет получить высокое качество разделения.

Тест Лямбда-Уилкса, результаты которого приведены в таблице 3, показывает, что средние значения дискриминирующих функций статистически значимо отличаются друг от друга. Уровень значимости менее 0,001 (в таблице 0,000) указывает на очень значимые различия.

Таблица 3

Тест Лямбда-Уилкса

В таблицах 4 и 5 приведены нормированные и ненормированные коэффициенты дискриминирующих функций. Нормированные коэффициенты дают полное представление о силе связи между переменными и дискриминирующими функциями, а также о направлении связи, а таблица нормированных коэффициентов должна использоваться при выполнении конкретных расчетов значений дискриминирующих функций.

Таблица 4

Нормированные коэффициенты канонической дискриминантной функции

Анализ таблиц 1-5 показывает, что наибольшее влияние на разделение спортсменов по специализации оказывают переменные: цветной показатель, количество лейкоцитов, спонтанный NST-тест нейтрофилов (активность). Последний показатель характеризует готовность нейтрофилов к респираторному взрыву (резкое усиление окислительного метаболизма) в активированных фагоцитах, ведущего к образованию широкого спектра первичных (супероксидный анион, перекись водорода, гидроксильный радикал, синглетный кислород) и вторичных (гипохлорная кислота, хлорамин, продукты перекисного окисления липидов) метаболитов, обладающих мощной бактерицидной активностью.

Таблица 5

Ненормированные коэффициенты канонической дискриминантной функции

Координаты центров групповых центроидов для трех дискриминирующих функций приведены в таблице 6.

Таблица 6

Координаты центров функций в центроидах групп

Разделение спортсменов по различным специализациям происходит в трехмерном пространстве, изображение которого на плоскости рисунка довольно неэффективно. Поэтому на рис. 2 приведены проекции результатов разделения на плоскость в координатах первых двух дискриминирующих функций.

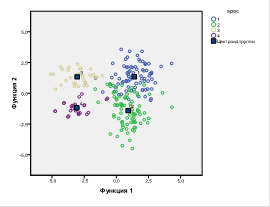
Рис. 2. Проекции результатов разделения на плоскость в координатах первых двух дискриминирующих функций.

Из рисунка 2 видно, что даже в проекции наблюдается хорошее разделение спортсменов по специализациям. В таблице 7 представлены результаты классификации спортсменов по специализациям с использованием 21-ой выбранной по результатам дискриминантного анализа переменных.

Таблица 7

Результаты классификации по 21 переменной

Как видно из таблицы 7, в среднем с вероятностью 0,923 можно предсказать спортивную специализацию.

5.3 Результаты дискриминантного анализа для специализации спортсменов (30 переменных по результатам факторного анализа, пошаговый метод). Аналогичный анализ был проведен для переменных, отобранных по результатам факторного анализа. Исходно таких переменных 30. В таблице 8 приведены собственные значения и коэффициенты канонической корреляции для трех дискриминирующих функций.

Таблица 8

Собственные значения и коэффициенты канонической корреляции

Как видно из таблицы 8, коэффициенты канонической корреляции немного ниже, но все равно достаточно высоки для корректной классификации. Тест Лямбда-Уилкса, результаты которого приведены в таблице, также показал высокие результаты.

Таблица 9

Тест Лямбда-Уилкса

В таблицах 9-12, аналогично изложенному выше, приведены нормированные и ненормированные коэффициенты дискриминирующих функций.

Таблица 10

Нормированные коэффициенты канонической дискриминантной функции

Анализ таблицы 10 показывает, что наибольшее влияние на разделение спортсменов по специализации оказывают переменные: средняя концентрация Hb в 1 эритроците, абсолютное количество нейтрофилов, лизосомальная активность нейтрофилов.

Таблица 11

Ненормированные коэффициенты канонической дискриминантной функции

Как видно из таблиц 9-10, результаты несколько отличаются от предыдущего случая, но все равно достаточно высоки для корректной классификации.

В таблице 11 приведены координаты центров групповых центроидов для полученных дискриминирующих функций.

Таблица 12

Координаты центров групповых центроидов групп

На рис. 3 приведены проекции результатов разделения на плоскость в координатах первых двух дискриминирующих функций.

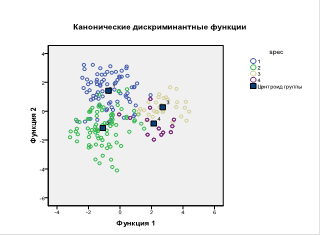
Рис. 3. Проекции результатов разделения на плоскость в координатах первых двух дискриминирующих функций по 15 переменным.

В таблице 13 представлены результаты классификации спортсменов по специализациям с использованием 15-ти переменных, выбранных по результатам дискриминантного анализа. Результаты несколько хуже, но все равно достаточно высоки, а число переменных можно уменьшить до 15. Таким образом, можно сократить размерность пространства в 4 раза.

Таблица 13

Результаты классификации с использованием 15-ти переменных

Средняя вероятность правильной классификации составляет 0,877.

Таким образом, дискриминантный и факторный анализ показали, что:

1. 30 показателей периферического отдела эритрона и иммунного статуса организма обеспечивают более 92 % объясненной дисперсии;

2. Наибольшее влияние на разделение спортсменов по специализациям оказывают переменные: цветной показатель, количество лейкоцитов, спонтанный NST-тест нейтрофилов (активность), средняя концентрация Hb в 1 эритроците, абсолютное количество нейтрофилов, лизосомальная активность нейтрофилов;

3. При использовании 21 переменной с вероятностью 0,923 (92,3%) можно предсказать спортивную специализацию, при использовании 15 переменных (что сокращает размерность пространства в 4 раза) средняя вероятность правильной классификации составляет 0,877 (87,7%).

Рецензенты:

Сабирьянов А.Р., д.м.н., профессор, заведующий кафедрой реабилитации и спортивной медицины ГБОУ ВПО «Южно-Уральский государственный медицинский университет» Минздрава России, г. Челябинск.

Колесников О.Л., д.м.н., профессор, заведующий кафедрой биологии ГБОУ ВПО «Южно-Уральский государственный медицинский университет» Минздрава России, г. Челябинск.