Введение
Мониторинг технического состояния воздушных линий электропередачи (далее – ЛЭП) ведется с целью сбора актуальной информации о параметрах технического состояния ВЛ в рамках выявления нарушений и неисправностей технического обслуживания. и включает в себя: осмотры, проверки, обследования опор и их фундаментов, проводов, грозозащитных тросов, линейной арматуры, изоляции, заземляющих устройств, контактных соединений, состояния подвесок и арматуры и др. [1; 2].
Контроль воздушных линий электропередачи можно проводить традиционным и дистанционным методами.
Традиционный метод контроля включает в себя визуальный осмотр без подъема и с подъемом на опоры.
Дистанционные методы контроля включают в себя:
- аэровизуальное инспектирование (фото- и видеосъемка) с помощью самолётов и вертолетов;
- спутниковый мониторинг, который основан на использовании снимков с ведущих действующих космических аппаратов.
Преимуществами дистанционного метода являются возможность обследования труднодоступных и протяженных участков ЛЭП с высокой скоростью, способность нести большую полезную нагрузку в виде контролирующих приборов, тепловизоров и др. Однако относительно высокая стоимость и невысокая точность (до 100 м) приводит к тому, что в последнее время при инструментальном дистанционном обследовании трасс электропередачи, кроме традиционных пилотируемых летательных аппаратов, получают распространение беспилотные летательные аппараты (БЛА), выполняемые по квадрокоптерной схеме (квадрокоптеры) [3-5] (рис. 1).
Обычно управление летательных аппаратов осуществляется с земли оператором, что значительно ограничивают область применения таких устройств. Кроме того, низкая грузоподъёмность не позволяет применять для мониторинга современное диагностическое оборудование. Дальнейшее распространение БЛА при мониторинге ЛЭП возможно при создании автономных летательных аппаратов, оснащённых интеллектуальными бортовыми САУ [2; 6].
Рис. 1. Проведение аэровизуального инспектирования
Создание алгоритмов автономного управления полётом квадрокоптера основано на методе математического моделирования движения квадрокоптера. Поэтому рассмотрим подробнее математическую модель квадрокоптера. При полёте квадрокоптера аэродинамические силы несущего винта представляют собой проекции продольной Нi, поперечной Si, подъёмной Тi сил винта на оси связанной системы координат Сxyz (рис. 2) [4-6].
Будем рассматривать движение корпуса робота в декартовой системе координат B, связанной с землей BXYZ, тогда положение центра масс аппарата определяют координаты вектора, связывающего С и В системы координат, задаваемые rB-матрицей rB=[X,Y,Z]T, а ориентацию в пространстве задают углы y, q, j, которые определяют ориентацию С-системы по отношению к В-системе координат, задаваемые QB-матрицей QB=[y, q, j,]T.
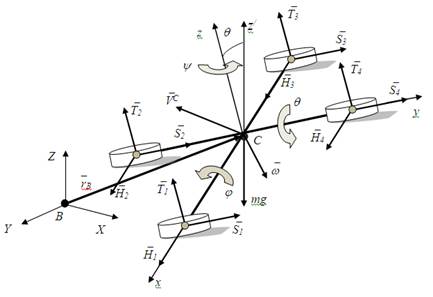
Рис. 2. Пространственная расчетная схема квадрокоптера
Уравнения, описывающие движение квадрокоптера, представлены в виде системы дифференциальных уравнений (1), которая описывает изменение обобщенных координат квадрокоптера в основных режимах движения [4-7].
В этих уравнениях: m – масса тела; 
– проекции ускорения центра масс квадрокоптера на оси ОХ, ОY, ОZ; JTP – сумма моментов инерции вращения вокруг оси винта; 
- осевые моменты инерции; где W1, W2,W3,W4 - угловые скорости соответственно переднего, правого, заднего, левого пропеллеров, W=-W1+W2-W3+W4 - суммарная угловая скорость 4-х пропеллеров квадрокоптера; l - расстояние между центром квадрокоптера и центром пропеллера; bi, d - аэродинамические постоянные; wx, wy, wz –проекции угловой скорости тела на оси неподвижной системы координат.
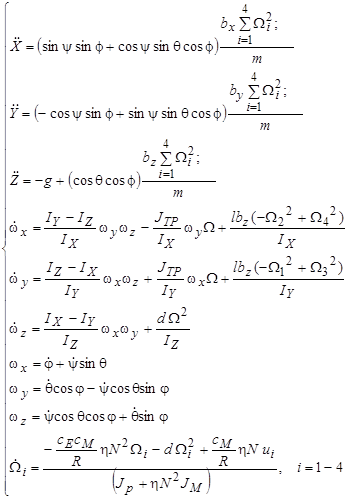(1)
Последние четыре уравнения системы (1) связывают управляющие напряжения, рассчитанные по алгоритму управления с угловыми скоростями вращения винтов, так как описывают взаимосвязанные электромагнитные и механические процессы в электромеханической системе приводов винтов квадрокоптера [4; 5]. Здесь обозначены: R – активное сопротивление обмотки ротора; ui – управляющие напряжения, wi - угловая скорость вращения вала электродвигателя; сЕ, cM - коэффициенты пропорциональности, называемый постоянной ЭДС и момента электродвигателя; Jp - приведенный осевой момент инерции; N= wi / Wi – передаточное отношение редуктора; h - КПД электропривода.
Моделирование движения квадрокоптера по заданной траектории
Будем считать, что режим движения определяется условием, при котором центр масс квадрокоптера C движется по заданной траектории и отклоняется от неё на величину, не превышающую dr (рис. 3). В режиме зависания положение центра масс квадрокоптера С в пространстве определяется радиус-вектором r, поэтому отклонение этой точки можно оценить коэффициентом позиционирования 
.
Алгоритм управления построен таким образом, что при x> x0, где x0 - параметр, определяющий точность позиционирования, на электродвигатели квадрокоптера подаётся соответствующее напряжение, обеспечивающее возврат квадрокоптера в область x< x0.
Реальное положение квадрокоптера в пространстве определяется системой датчиков.
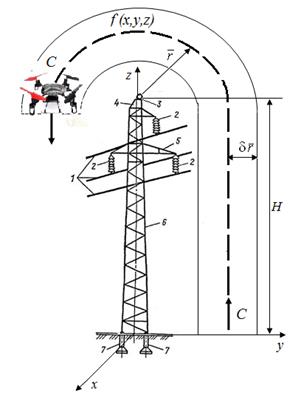
Рис. 3. Облёт квадрокоптером промежуточной металлической опоры одноцепной линии:
1 – провода; 2 – изоляторы; 3 – грозозащитный трос; 4 – тросостойка; 5 – траверсы опоры;
6 – стойка опоры; 7 – фундамент опоры
Моделирование траектории облета квадрокоптером опоры ЛЭП
Рассмотрим автономный облёт опоры ЛЭП по заданной траектории, позволяющий осуществить мониторинг состояния в автоматическом режиме [1; 2].
Разобьем траекторию облёта квадрокоптером опор ЛЭП на три этапа: 1 – взлёт, 2 – облет по заданной траектории в различных плоскостях с зависанием, 3 – спуск или посадка, и рассмотрим каждый из них.
Первый этап. 0 £ z £ H, х=х0, y=y0, z=z(t), где х0,y0 – параметры взлёта.
Отрыв квадрокоптера от поверхности, или начало полета происходит, если выполняется условие: нормальная реакция опоры R=0 (рис. 4).
Пусть взлёт квадрокоптера от поверхности происходит по следующему закону:
, (2)
а закон изменения скорости:
, (3)
где a, b, c – постоянные, определяемые из граничных условий:
при 
(4)
при 
(5)
Решая уравнения (2) и (3) с учетом (4), (5), определяем уравнение, описывающее вертикальный подъем коптера на высоту H за время t1 :
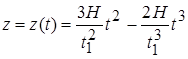. (6)
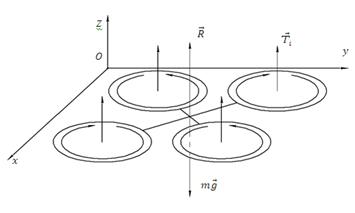
Рис. 4. Отрыв квадрокоптера от поверхности: R – нормальная реакция опоры поверхности, Тi – тяговое усилие винта, mg - вес квадрокоптера
2 этап. Для облета ВЛ в вертикальной плоскости: Н £ z £ (Н+r), х=0, y=y0(t), z=z(t).
Уравнение траектории движения имеет вид: (z - H)2 + y 2= r2.
Для облета ВЛ в горизонтальной плоскости: z=Н, х=±х0(t), y=±y0(t),.
Уравнение движения имеет вид: x2 + y 2= r2.
3 этап. H ³ z ³ 0, х=х1, y= y1, z=z(t), где х1, y1 - координаты посадки. Данный этап аналогичен первому этапу.
Спуск с высоты Н за время t1, равное времени подъёма по заданному закону:
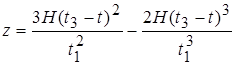, (7)
где t1, t3 - время взлёта и посадки квадрокоптера. Тогда T=åti – общее время полёта.
Далее проводилось численное моделирование режима взлёта, висения и приземления квадрокоптера. Примеры реализации различных режимов движения показаны на рис. 5.
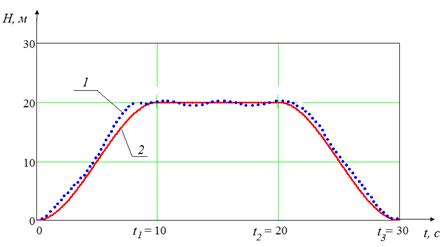
Рис. 5. График режима взлёта, висения и приземления квадрокоптера во времени:
1 - реальный, 2 - теоретический; t1, t2, t3 - время взлёта, зависания или облёта и посадки квадрокоптера соответственно.
Анализ графика на рис. 5 показывает, что использование пропорционального регулятора позволяет обеспечить движение квадрокоптера по заданной траектории с погрешностью dr , не превышающей допустимой.
Выводы
Автоматизация процесса мониторинга ЛЭП позволит без участия оператора получить уникальную фото- и видеоинформацию, в кратчайшие сроки оценить и проанализировать общее состояние линейных объектов энергетической инфраструктуры, а впоследствии – прогнозировать и моделировать природные воздействия на линии, определять дефекты, отклонения проводов и изоляции от допустимых норм.
Рецензенты:
Локтионова О.Г., д.т.н., доцент, проректор по учебной работе Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Юго-Западный государственный университет», г. Курск.
Кобелев Н.С., д.т.н., профессор, заведующий кафедрой теплогазоснабжения и вентиляции Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Юго-Западный государственный университет», г. Курск.