Введение
Определение координат источника светового излучения обычно осуществляется путем измерения отклонения его изображения в фокальной плоскости от фокуса оптической системы. Турбулентность среды распространения значительно снижает точность определения координат и приводит к тому, что тактико-технические характеристики современных оптических измерительных систем (ОИС) значительно отличаются от потенциально возможных. В настоящее время разработан аппарат фазового сопряжения [1, 2, 3, 4, 5], позволяющий эффективно компенсировать нестационарные возмущения световых пучков при их распространении в возмущенных каналах. Поэтому для повышения точности определения параметров движения объекта оптическими измерительными системами целесообразно объединить задачу пеленгации с задачей компенсации нестационарных искажений принимаемого оптического сигнала.
Целью данной работы является разработка методов определения параметров движения объекта при проведении траекторных измерений оптическими системами в турбулентной атмосфере при интенсивных шумах регистрации на основе комплексного применения методов адаптивной оптики и додетекторной квазиоптимальной пространственной обработки пуассоновских оптических полей.
Определение угловых координат подвижного объекта будем проводить следующим образом:
- по результатам измерений датчика Гартмана проведем восстановление фазового фронта отраженного от объекта оптического сигнала;
- определим аберрации первого порядка, представляющие собой наклоны фазового фронта в двух перпендикулярных плоскостях;
- по значениям наклонов фазового фронта проведем расчет азимута и угла места подвижного объекта.
При этом источник излучения будем считать точечным, поскольку предполагается, что сигнал будет отражаться оптическим уголковым отражателем, установленным на объекте. В случае определения координат протяженного объекта, в процессе поиска и фокусировки ОИС может быть настроено на одно из ярких интерференционных пятен, сформировавшихся на поверхности объекта, а источник излучения также можно полагать точечным.
Синтез алгоритмов определения угловых координат подвижного объекта
Рассмотрим задачу определения угловых координат в следующей постановке. В результате восстановления фазового фронта адаптивной оптической системой (АОС) имеется набор значений фазы 
на апертуре входного зрачка, представляющих собой реализации случайных величин 
, полученные по результатам измерений датчика фазового фронта в ходе их обработки по одному из представленных выше алгоритмов. Поскольку аберрации фазового фронта первого порядка описываются линейными функциями, то определить их значения в данном случае можно, аппроксимируя восстановленный фазовый фронт функцией вида
, (1)
Для решения этой задачи применим метод максимального правдоподобия, поскольку данный метод приводит к сравнительно простому математическому способу определения коэффициентов 
и не создает трудностей для его реализации в реальном масштабе времени [6, 7, 8, 9, 10]. Следует напомнить, что на выходе отдельного квадрантного фотоприемника, входящего в состав датчика гартмановского типа, присутствует слабый сигнал, имеющий пуассоновское распределение [3]. Однако специфика датчиков гартмановского типа такова, что для получения оценок средних наклонов фазового фронта по субапертуре, используемых в дальнейшем при восстановлении фазы на всей апертуре датчика, проводится суммарно-разностная обработка сигналов с выхода каждого квадрантного фотоприемника. Синтезированные алгоритмы восстановления фазового фронта в свою очередь проводят линейную обработку измерений датчика Гартмана. Из этого следует, что в рассматриваемом случае применима центральная предельная теорема, в соответствии с которой полученные оценки фазы оптического сигнала можно считать нормальными.
Рассмотрим значение аргумента 
. Результат восстановления есть случайная величина с математическим ожиданием 
и среднеквадратическим отклонением 
. Поскольку фотоприемники датчика Гартмана идентичны, а обработка измерений ведется по общему алгоритму, то можно положить все среднеквадратические отклонения одинаковыми и равными 
. Тогда закон, по которому распределяется величина , имеет вид
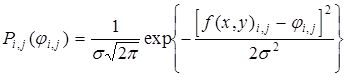. (2)
В результате восстановления фазового фронта произошло следующее событие: случайные величины приняли значения . В соответствии с принципом максимального правдоподобия задача аппроксимации заключается в получении такого математического ожидания , чтобы вероятность этого события была максимальной.
Строго говоря, вероятность событий = равна нулю, так как значение фазы на апертуре непрерывно. По этой причине будем вести речь не о вероятности событий, а о соответствующих элементах вероятностей
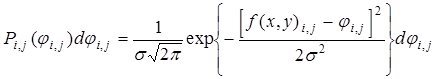. (3)
Тогда вероятность того, что система случайных величин примет совокупность значений, лежащих в пределах (;+
), запишется как
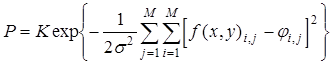, (4)
где К – некоторый коэффициент, независящий от .
Очевидно, что для максимизации выражения (2.55) необходимо, чтобы показатель степени в нем был минимален. Отсюда, отбрасывая постоянный множитель и учитывая (3), получим условие максимального правдоподобия для оценки наклонов фазового фронта
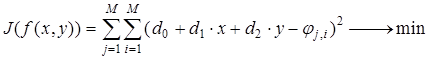(5)
Приравнивая нулю производные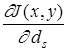 
, 
, получим систему линейных уравнений для определения коэффициентов 
;
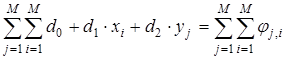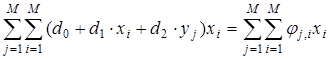; (6)
.
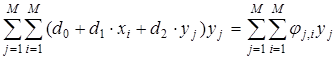Система (6) в матричной форме запишется в виде
. 
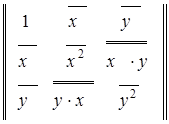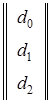
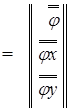, (7)
где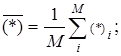 
.
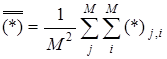Решая (7) одним из известных методов, получим значения средних наклонов фазового фронта в плоскостях zoy и zox соответственно
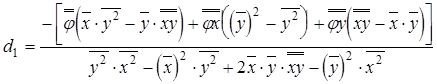, (8)
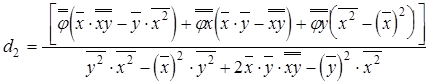, (9)
Уравнение нормали к поверхности F(x,y,z) в точке A(X,Y,Z) в общем виде определяется выражением:
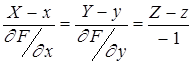, (10)
Тогда, учитывая, что направление нормали к плоскости не зависит от координат точки, в которой она восстановлена, уравнение нормали к плоскости запишется в виде
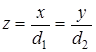. ( 11)
Подставляя (9) и (10) в (11), получим выражение для линии визирования ОИС
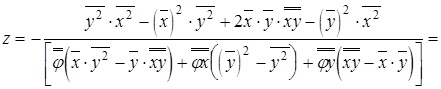
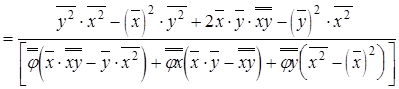. (12)
В этом случае оценки азимута и угла места объекта запишутся как
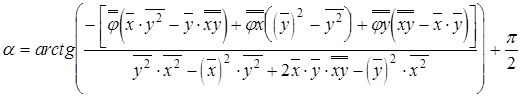, (13)
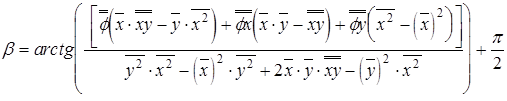. (14)
Таким образом, выражения (13) и (14) представляют собой угловые координаты объекта, полученные на основе метода фазового сопряжения.
Выводы
В настоящей работе синтезирован алгоритм совместной компенсации нестационарных искажений оптического излучения, вызванных его распространением в турбулентной атмосфере и измерения угловых координат источника этого излучения. Определение угловых координат осуществляется на базе метода максимального правдоподобия, чем обеспечивается минимизация среднеквадратического отклонения полученных оценок от истинного значения пеленга подвижного объекта. Синтезированный алгоритм предназначен для реализации в АОС фазового сопряжения. Размеры датчика фазового фронта существенно влияют на точность получаемых оценок угловых координат. Наиболее сильно такое влияние оказывается в случае слабой турбулентности. Это объясняется тем, что в случае слабой турбулентности к размерам датчика более чувствительна точность восстановления фазового фронта, являющаяся, в свою очередь, составной частью точности измерения угловых координат.
Рецензенты:
Звездина М.Ю., д.ф.-м.н., доцент, зав. кафедрой «Радиоэлектроника», Минобрнауки России, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Донской государственный технический университет», г. Ростов-на-Дону.
Габриэльян Д.Д., д.т.н., профессор, заместитель начальника научно-технического комплекса «Антенные системы» по науке, Федеральный научно-производственный центр ФГУП «РНИИРС», г. Ростов-на-Дону.