Введение
Для решения задач теплопроводности применяют аналитические и численные методы. Аналитические методы состоят в подборе уравнения процесса, удовлетворяющего дифференциальному уравнению теплопроводности и краевым условиям. Из аналитических методов наиболее часто применяются методы интегральных преобразований (преобразования Ханкеля, Лапласа, Фурье) и метод источников.
В настоящее время наиболее распространенным является численный метод конечных элементов (МКЭ, или FEM). Современные программные продукты, например, ANSYS, COMSOL предоставляют широкие возможности расчета теплопроводности при сварке. Численный метод не дает, подобно аналитическому, общего решения задачи, но его целесообразно применять для инженерных расчетов в тех случаях, когда получение аналитического решения ввиду сложности условий задачи становится крайне трудоемким или вообще недоступным.
Сущность плазменной поверхностной термообработки заключается в высокоскоростном локальном нагреве участка поверхности до высоких температур и последующим охлаждением со сверхкритической скоростью за счет теплоотвода во внутренние слои материала изделия. При этом формируется структура с высокими эксплуатационными характеристиками [2]. Технологические параметры процесса плазменной поверхностной термообработки включают в себя величину и полярность тока, скорость перемещения плазмотрона относительно изделия, расход защитного и плзазмообразующего газов, диаметр плазмообразующего сопла [3]. Упрочнение поверхности заданной площади достигается последовательным формированием локальных зон закалки в виде протяженных полос встык.
Учет действительной формы изделия может значительно усложнить решение температурных задач плазменной поверхностной термообработки. Поэтому реальную форму в тепловых расчетах идеализируют, сводя ее к одной из следующих тепловых схем, для которых решение уравнения теплопроводности можно получить в аналитическом виде. В нашем случае рассматривается полубесконечное тело.
Материалы и методы исследования
Теплопередача в изделие при работе плазмотрона на обратной полярности определяется приэлектродными процессами и передачей тепла плазменным потоком и может быть представлена в виде:
![]() (1.1)
(1.1)
uк – катодное падение напряжения;
φв – работа выхода;
Pп – мощность передаваемая изделию плазменным потоком;
Iд – сила тока плазменной дуги
При работе плазматрона на обратной полярности зона контакта дуги представляет собой совокупность достаточно большого числа относительно малых по размеру, но разрозненных нестационарных пятен различного типа, высокую температуру имеет только та часть поверхности, на которую опираются пятна дуги, а остальная часть остается относительно холодной. Одной из отличительных особенностей нестационарных пятен является кратковременность их существования и большая плотность тока в них (j~105-106Acм-2). Последнее означает, что удельные тепловые потоки достигают значений (q~106-107 Вт/см2), таким образом достигаются необходимые для поверхностной закалки скорости нагрева и охлаждения. Катодные пятна не привязаны к одному месту, они блуждают по всей зоне обработки, ограниченной величиной полутора диаметров защитного сопла, таким образом достигается более равномерный нагрев поверхности.
Исходя из всего вышесказанного предлагается при расчете температурных полей при обработке на обратной полярности использовать комбинированный источник нагрева.
Тепло, передаваемое плазменным потоком, представим в виде поверхностного источника нагрева с нормальным распределением теплового потока в пятне нагрева радиусом r [1] :
![]() (1.2)
(1.2)
![]() – удельный тепловой поток в любой точке пятна нагрева;
– удельный тепловой поток в любой точке пятна нагрева;
![]() – наибольший удельный тепловой поток в центре пятна нагрева;
– наибольший удельный тепловой поток в центре пятна нагрева;
k – коэффициент сосредоточенности теплового потока.
Учитывая быстрое и хаотичное движение катодных пятен, кратковременность их существования, при допущении равномерного распределения вероятности возникновения катодного пятна в пределах зоны контакта дуги с металлом, совокупное действия катодных пятен можно при моделировании заменить равномерно распределенным поверхностным источником тепла.
Математическая модель основана на решении дифференциального уравнения переноса энергии:
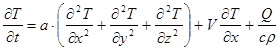 (1.3)
(1.3)
Q – эффективная тепловая мощность дуги Вт;
V – скорость обработки м/ч;
а – коэффициент температуропроводности м2/с;
с – удельная теплоемкость Дж/кг*К
r – плотность материала кг/м3
Дифференциальное уравнение переноса энергии является математической моделью целого класса явлений теплопроводности и имеет бесконечное множество решений. Чтобы получить из этого множества одно частное решение, характеризующее конкретный процесс, необходимо иметь дополнительные данные, не содержащиеся в исходном дифференциальном уравнении. Эти дополнительные условия, которые в совокупности с дифференциальным уравнением определяют конкретную задачу, называются условиями однозначности:
1) Граничные условия третьего рода:
3) Набор теплофизических характеристик: с, λ, ρ, а;
4) Температура в начальный момент времени равна 20°С.
Зная:
![]() , (1.4)
, (1.4)
q1 – мощность передаваемая потоком плазмы, Вт;
q2 – удельная мощность, передаваемая за счет катодных пятен Вт/м2.
f – площадь блуждания катодных пятен, м2;
Результаты исследования и их обсуждения
Таким образом, решив систему уравнений в системе COMSOL [4] Multiphysics, получаем следующий результат:
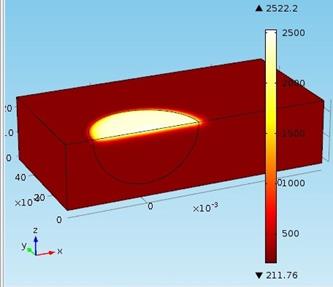
Рис.1. Температурное поле на поверхности образца.
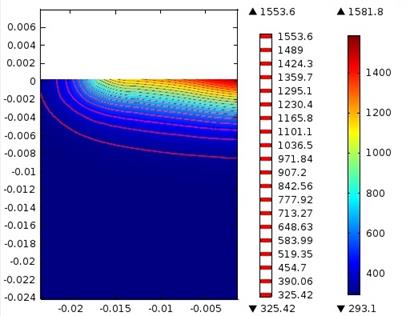
Рис.2 . Распределение температур по сечению образца.
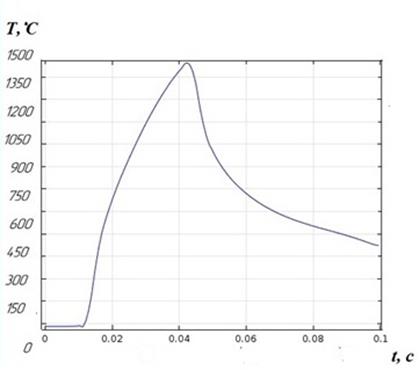
Рис.3. Термический цикл нагрева – охлаждения при действии комбинированного источника теплоты.
Таким образом, полученные после корректировки температурные поля, а также термический цикл нагрева-охлаждения, показывают эффективность такой обработки.
По результатам проведенных исследований [5] установлено, что при работе плазмотрона на токе обратной полярности в области малых токов теплопередача в изделие осуществляется в основном за счет тепловыделения в катодных пятнах. Исходя из вышесказанного представляют интерес тепловые процессы на поверхности изделия при воздействии одного пятна.
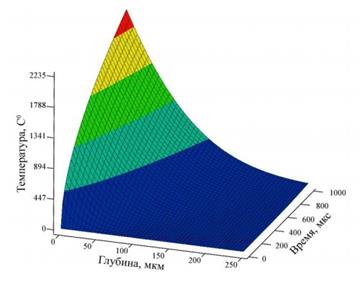
Рис.4. Распределение температуры поверхности по глубине нагрева.
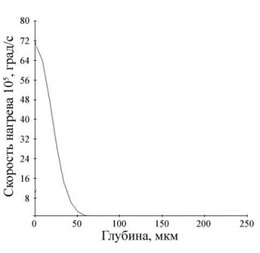
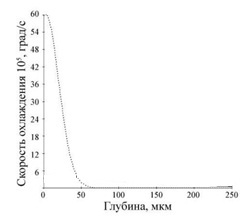
Рис.5. Скорости нагрева и охлаждения по глубине при воздействии одного пятна.
Выводы
Таким образом, плазменная поверхностная закалка на токе обратной полярности может использоваться для получения упрочненных слоев без оплавления поверхности глубиной около 2 мм либо для получения тонких упрочненных слое глубиной около 0.25 мм при использовании малоамперной дуги. Кроме того, благодаря высоким градиентам температур, создаваемым на поверхности изделия блуждающими катодными пятнами, применение обратной полярности целесообразно в процессах плазменной наплавки для увеличения ширины наплавляемых валиков и снижения доли участия основного металла в наплавленном.
Работа выполнена при поддержке гранта РРФФИ №13-08-00397A, при финансовой поддержке со стороны Минобрнауки России в рамках базовой части и Министерства образования Пермского края.
Рецензенты:
Беленький В.Я., д.т.н., профессор, декан Механико-технологического факультета ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г.Пермь.
Синани И.Л., д.т.н., профессор кафедры Механико-технологического факультета ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г.Пермь.



