Основными направлениями совершенствования современного заочного высшего образования являются внедрение новых, современных систем обучения (информационных образовательных интернет-технологий), повышение качества заочного высшего образования и контроля знаний с использованием дистанционных образовательных технологий (ДОТ) [4; 6; 7; 9; 10].
В данной работе аналогично [1-3; 5; 8] проведен многомерный статистический анализ результатов оценивания знаний по высшей математике (выборка ЭНИН1 объема n =248) в объеме 1-го семестра (линейная алгебра и аналитическая геометрия) студентов заочной формы обучения с использованием ДОТ Энергетического института Томского политехнического университета. Рассмотрение проведено в системе 3 показателей (рис. 1): ИДЗ – оценка выполнения 4 индивидуальных домашних заданий (по 5-балльной шкале), ЭКЗ – результат тест-экзамена в режиме online (по 5-балльной шкале) и DT – разность моментов окончания и начала экзамена (в минутах).
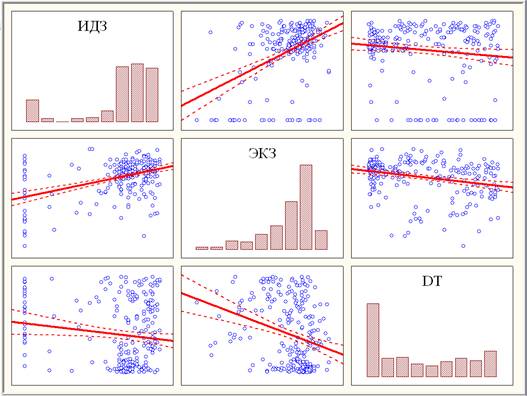
Рис. 1. Диаграммы рассеяния с прямыми регрессии и гистограммами переменных выборки ЭНИН1
В сравнении с [3] доля «неуд» (ЭКЗ<2,5) уменьшилась в »1,5 раза (с 16,2 до 10,5%), доля положительно сдавших тест-ЭКЗ за DT < 20 минут из выделенных 3 часов возросла в »1,5 раза (с 20 до 31%). Среди сдавших ЭКЗ установлен новый рекорд минимального DT, = 4 мин.
Выявленное аномальное обстоятельство лишний раз подчеркивает несовершенство стадии оценивания усвоенных студентом знаний при дистанционном обучении с использованием ДОТ, создающее проблему идентификации студента [1; 3; 6].
В рамках корреляционного анализа выявлены высоко значимые (на уровне значимости р < 0,0005) положительная корреляционная зависимость между ИДЗ и ЭКЗ (коэффициент корреляции Пирсона r = 0,44) и отрицательная – между DT и ЭКЗ (r = - 0,28) при критическом r » 0,12 (на уровне значимости р = 0,05 для n =248).
С учетом корреляционной зависимости исходных показателей (ИДЗ, ЭКЗ и DT) на основании факторного анализа проведено сокращение их числа до двух (Ф1 и Ф2) и проведена интерпретация новых переменных по нагрузкам, характеризующим корреляции между факторами и показателями (табл. 1).
Таблица 1
Вращаемые факторные нагрузки в выбранной 2-факторной модели ЭНИН1
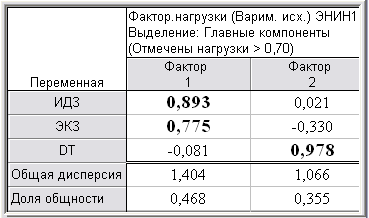
Согласно табл. 1, высокие факторные нагрузки исходных показателей распределились по факторам следующим образом.
Фактор Ф1 – фактор успеваемости {ИДЗ+ЭКЗ} характеризуется положительной корреляционной связью.
Фактор Ф2 – фактор времени DT выполнения тест-ЭКЗ характеризуется положительной корреляционной связью.
Для проведения дальнейшего анализа ЭНИН1 в рамках построенной 2-факторной модели вычислены значения наблюдений в новой системе факторных координат.
В построенном 2-мерном факторном пространстве {Ф1, Ф2} методом K-средних, проводящим классификацию объектов по заданному количеству кластеров, получена 7-кластерная высококачественная модель результатов ЭНИН1, распределяющая 248 студентов по 7 кластерам высоко значимо (на уровне значимости р < 0,0005) согласно λ-критерию Уилкса по совокупности показателей Ф1 и Ф2 (рис. 2).
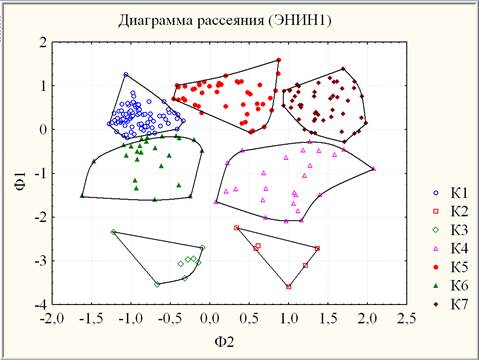
Рис. 2. Диаграмма рассеяния кластеров ЭНИН1 в факторных координатах {Ф1, Ф2}
Алгоритм метода K-средних, перемещая объекты в разные кластеры с целью минимизации изменчивости внутри кластеров и максимизации изменчивости между кластерами, оценивает качество кластеризации наблюдений по каждому фактору посредством параметрического дисперсионного анализа (табл. 2).
Таблица 2
Результаты дисперсионного анализа кластеризации наблюдений по факторам ЭНИН1
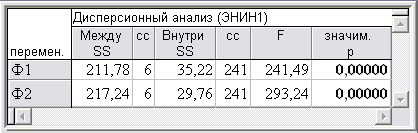
Таблица 2 свидетельствует о высоком качестве (на уровне значимости р < 0,0005) группировки 248 студентов в 7 кластеров по каждому фактору. Полученные результаты (табл. 4) подтверждаются непараметрическим однофакторным дисперсионным анализом на основе критерия Краскела-Уоллиса и медианного теста.
Кластерные средние по старым {ИДЗ, ЭКЗ, DT} и новым {Ф1, Ф2} показателям приведены в табл. 3.
Таблица 3
Кластерные средние по ИДЗ, ЭКЗ (5-балльная шкала), Ф1, Ф2 (стандартизированные) и DT (минуты)
|
Кластер |
ИДЗ |
ЭКЗ |
Ф1 |
Ф2 |
DT |
n |
|
К1 |
3,911 |
4,122 |
0,288 |
-0,915 |
17,699 |
93 |
|
К2 |
0,181 |
1,514 |
-2,841 |
0,856 |
134,333 |
6 |
|
К3 |
0,115 |
1,638 |
-3,000 |
-0,411 |
57,625 |
8 |
|
К4 |
2,050 |
2,714 |
-1,174 |
0,985 |
137,880 |
25 |
|
К5 |
4,424 |
4,194 |
0,761 |
0,226 |
84,488 |
43 |
|
К6 |
2,707 |
3,499 |
-0,648 |
-0,761 |
31,960 |
25 |
|
К7 |
4,333 |
3,655 |
0,565 |
1,416 |
153,104 |
48 |
Графики кластерных средних для каждого фактора приведены на рис. 3.
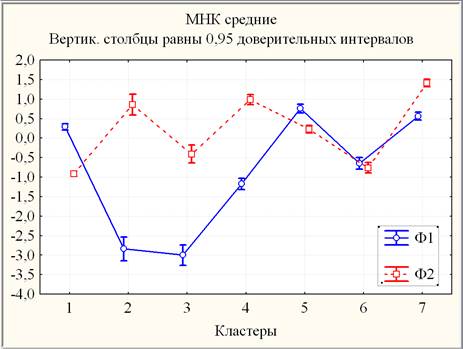
Рис. 3. Линейные графики факторных (стандартизированных) средних с 95% границами доверительных интервалов для каждого кластера
Согласно апостериорным критериям (Фишера, Шеффе, Тьюки) можно оформить результаты множественных сравнений кластерных средних в порядке их убывания для каждого фактора:
Ф1: {К5, К7}, {К1}, {К6}, {К4}, {К2, К3} так, что К7 (mK7»0,565) отличается от К1(mK1»0,288) сильно значимо (на уровне значимости 0,0005< р < 0,005).
Ф2: {К7}, {К4, К2}, {К5}, {К3, К6}, {К6, К1} так, что К3 (mK3»-0,411) отличается от К1 (mK1»-0,915) сильно значимо (на уровне значимости 0,0005< р < 0,005).
Построенные последовательности неоднородных групп кластеров по каждому фактору находятся в согласии с результатами множественных сравнений по непараметрическому критерию Краскела-Уоллиса.
Результаты кластерного анализа наблюдений по совокупности факторов с учетом результатов множественных сравнений кластерных средних для каждого фактора позволяют провести классификацию наблюдений в порядковой шкале стандартизированных измерений, полагая в качестве уровня «Средний» – стандартизированный интервал (-0,25; +0,25), «Выше среднего» – (+0,25; +1,25), «Ниже среднего» – (-1,5; -0,25) и «Аутсайдер» – (< -1,5).
Таблица 4
Классификация наблюдений по совокупности факторов в порядковой шкале стандартизированных измерений
|
Кластер |
Объем кластера |
Ф1 {ИДЗ+ЭКЗ} |
Ф2 {DT} |
|
К1 |
93 |
Выше среднего |
Ниже среднего |
|
К2 |
6 |
Аутсайдер |
Выше среднего |
|
К3 |
8 |
Аутсайдер |
Ниже среднего |
|
К4 |
25 |
Ниже среднего |
Выше среднего |
|
К5 |
43 |
Выше среднего |
Средний |
|
К6 |
25 |
Ниже среднего |
Ниже среднего |
|
К7 |
48 |
Выше среднего |
Выше среднего |
Согласно рис. 2-3 и табл. 4, кластерная модель результатов оценивания знаний по высшей математике имеет спектральную структуру. Даже среди условно допущенных (mИДЗ < 0,2) и не сдавших тест-экзамен (mЭКЗ < 1,7), то есть имеющих уровень «Аутсайдер» по успеваемости (mФ1 < -2,8), выделяются разные кластеры, значимо различающиеся по DT, то есть по Ф2: 8 студентов К3 (mDT » 58 или mФ2 » -0,41) и 6 студентов К2 (mDT » 134 или mФ2 » 0,86). Аналогично среди успешно допущенных (mИДЗ > 3,9) и успешно сдавших тест-экзамен (mЭКЗ > 3,6), то есть имеющих уровень «Выше среднего» по успеваемости (mФ1 > 0,28), выделяются 3 кластера, значимо различающиеся по DT, то есть по Ф2: 93 «легкодума» К1 (mDT » 18 или mФ2 » -0,92), и 43 «среднедума» К5 (mDT » 84 или mФ2 » 0,23) и 48 «тугодумов» К7 (mDT » 153 или mФ2 » 1,42). Наличие самого массового кластера «успешных легкодумов» К1 в сравнении с аналогичными результатами в [3] свидетельствует об обострении проблемы идентификации оцениваемого студента. Заметим, что из 12 учебных групп ЭНИН1 основной вклад в кластер «успешных легкодумов» К1 вносят 4 учебные группы, выделяющиеся на фоне остальных географией набора.
По-прежнему острой проблемой оценивания усвоенных студентом-заочником знаний в режиме ДОТ является чрезмерное увлечение автоматизацией (практически без участия преподавателя) итогового контроля знаний обучаемых в условиях несовершенства содержания и формы тестовых заданий, что приводит к завышению на целый балл (по 5-балльной шкале) результатов оценивания усвоенных студентом-заочником знаний в режиме ДОТ по сравнению с классическим режимом [1].
Выводы
1. В рамках корреляционного анализа выявлены высоко значимые (на уровне значимости р < 0,0005) положительная корреляционная зависимость между ИДЗ и ЭКЗ (коэффициент корреляции Пирсона r = 0,44) и отрицательная – между DT и ЭКЗ (r = - 0,28).
2. С учетом корреляционной зависимости показателей на основании факторного анализа построены Ф1 – фактор успеваемости {ИДЗ+ЭКЗ} и Ф2 – фактор времени DT выполнения тест-ЭКЗ.
3. В 2-мерном факторном пространстве {Ф1, Ф2} методом K-средних получена 7-кластерная значимая модель, распределяющая 248 студентов по 7 кластерам.
4. В рамках дисперсионного анализа выделены для каждого фактора однородные (различающиеся незначимо) группы кластеров.
5. Проведена классификация результатов оценивания усвоенных студентом знаний по высшей математике при дистанционном обучении с использованием ДОТ в номинальной шкале измерений.
6. Результаты подобной кластеризации результатов оценивания знаний могут быть учтены при внедрении современных информационных образовательных интернет-технологий в организацию заочного обучения для обеспечения качества образования и контроля знаний.
Работа выполнена при поддержке Российского научного фонда.
Рецензенты:
Трифонов А.Ю., д.ф.-м.н., профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск.
Арефьев К.П., д.ф.-м.н., профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск.



