Введение
Контактно-поверхностные теплообменные аппараты, работающие в изотермических условиях в объеме контактной камеры, позволяют получать экономию тепловой энергии и повысить эффективность очистки обрабатываемых газов от нежелательных токсичных примесей или поддерживать наилучшие технологические режимные параметры процесса.
Правильное прогнозирование значения коэффициента теплоотдачи в слое насадки, пронизываемом потоком двухфазной среды (газа и жидкости), имеет большое значение в инженерной практике проектирования и анализа работы теплообменных аппаратов с насадкой. Критериальные уравнения, характеризующие теплоотдачу между газожидкостной средой (ГЖС) и стенкой теплообменного элемента, справедливы только для частных случаев теплообмена и не могут быть признаны обобщающими.
Цель исследования в слое насадки. Целью данной работы является получение аналитического решения критериального уравнения теплообмена между ГЖС и охлаждающим элементом контактно-поверхностных теплообменных аппаратов.
Методы исследования. Теоретическая часть работы базируется на изучении механизмов теплопередачи. Адекватность математической модели обеспечивается совместным использованием классических закономерностей для вывода критериального уравнения, описывающего закономерности теплоотдачи от газожидкостной смеси к поверхности погруженного охлаждающего элемента с позиции аналогии с теорией барботажа.
Как известно [3], при развитом пенном режиме барботажа интенсивно турбулизован весь объем ГЖС. Температура ядра газожидкостного потока при этом постоянна, толщина пленки жидкости достигает здесь своего минимального значения, остается постоянной и независимой от скорости газа. Соответственно этому должно сохраняться постоянство термического сопротивления слоя, а, следовательно, и коэффициента теплоотдачи. Таким образом, рассматриваются две области с четко выраженной границей между интенсивно движущейся ГЖС с постоянной температурой по всему объему смеси и медленно движущейся пленкой жидкости, в которой имеет место резкое изменение температуры от температуры смеси на внешней границе пленки до температуры на поверхности теплообменного элемента. Принято считать, что протекание процессов теплопередачи в пленке носит нестационарный характер [3, 7]. Нестационарность обусловлена как турбулентными пульсациями, если они есть, вызванные внутренней неустойчивостью, так и изменением во времени внешней границы пленки в связи с движением пузырей газа. Поэтому в модель необходимо ввести нестационарные уравнения Навье – Стокса и уравнение энергии.
Условная средняя толщина пленки может быть найдена по формулам, предложенным в [5]:
![]() (1)
(1)
Предварительные расчеты показали, что она составляет от 172,2 мк. до 257,2 мк. при ![]() равной от 60 м2/с до 200 м2/с.
равной от 60 м2/с до 200 м2/с.
Скорость течения пленки изменяется по ее толщине по параболическому закону (от нуля у стенки до ![]() у свободной поверхности) и определяется по формуле [5]:
у свободной поверхности) и определяется по формуле [5]:
![]() (2)
(2)
где ![]() – линейная плотность орошения, м2/с,
– линейная плотность орошения, м2/с,
![]() – приведенная толщина пленки.
– приведенная толщина пленки.
При минимальной плотности орошения ![]() = 0,097 м/с, а при максимальной плотности орошения
= 0,097 м/с, а при максимальной плотности орошения![]() = 0,216 м/с.
= 0,216 м/с.
По сравнению с диаметром применяющихся теплообменных элементов толщина пленки очень мала. Так как отношение ![]() и радиус кривизны элемента не претерпевает резких изменений (исключается влияние шероховатости стенки), можно в данном случае рассматривать плоскую задачу теплообмена через пленку вязкой жидкости [3]. Отсюда очевидна независимость коэффициента теплоотдачи от диаметра элемента.
и радиус кривизны элемента не претерпевает резких изменений (исключается влияние шероховатости стенки), можно в данном случае рассматривать плоскую задачу теплообмена через пленку вязкой жидкости [3]. Отсюда очевидна независимость коэффициента теплоотдачи от диаметра элемента.
Рассмотрим распределение температур и скоростей в вязком слое пленки, образующемся в условиях, аналогичных развитому пенному режиму барботажа.
Если ось «х» направить вдоль пристенной поверхности пленки, а ось «у» – перпендикулярно слою, то для плоской задачи распределение температур будет характеризоваться [8] уравнением теплопроводности:
![]() , (3)
, (3)
где ![]() – коэффициент температуропроводности, м2/с.
– коэффициент температуропроводности, м2/с.
Распределение скоростей для общего случая неустановившегося двухмерного потока определяется уравнением Навье – Стокса и уравнением неразрывности:
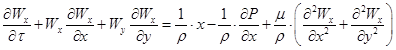 , (4)
, (4)
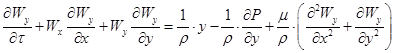 , (5)
, (5)
![]() . (6)
. (6)
Проанализируем систему уравнений (4) – (6) применительно к случаю движения в тонком слое пленки. Влиянием турбулентных пульсаций на нестационарность тепловых процессов в слое пленки можно пренебречь, если число Рейнольдса для этого слоя меньше критического значения ![]() . Сделанные выше ориентировочные расчеты числа Рейнольдса для пленки позволяют оценить возможный интервал значений (от минимального
. Сделанные выше ориентировочные расчеты числа Рейнольдса для пленки позволяют оценить возможный интервал значений (от минимального ![]() до максимального
до максимального ![]() ). Таким образом, действительные значения гораздо меньше критического, что позволяет сделать вывод о возможности не учитывать турбулентные пульсации в слое пленки, вызванные внутренней неустойчивостью потока.
). Таким образом, действительные значения гораздо меньше критического, что позволяет сделать вывод о возможности не учитывать турбулентные пульсации в слое пленки, вызванные внутренней неустойчивостью потока.
Нестационарность во времени внешней границе пленки определяется [6] критерием Струхаля (гидродинамической гомохронности):
![]() , (7)
, (7)
где ![]() – толщина пленки, мк;
– толщина пленки, мк;
![]() – частота изменения формы внешней границы пленки, сек;
– частота изменения формы внешней границы пленки, сек;
![]() – скорость жидкости на внешней границе слоя пленки, м/с.
– скорость жидкости на внешней границе слоя пленки, м/с.
В рассматриваемом случае эта частота изменения внешней границы будет характеризоваться временем прохождения пузыря:
![]() , (8)
, (8)
где ![]() – диаметр газового пузыря, м;
– диаметр газового пузыря, м;
![]() – скорость подъема пузыря, м\с.
– скорость подъема пузыря, м\с.
Принимая средний размер газовых пузырей равным эквивалентному диаметру пустот насадки ![]() =0,015 м (для сферических элементов насадки диаметром 30 мм), скорость подъема пузырей согласно [5] равной 2 м/с, скорость жидкости на внешней границе пленки согласно вышеприведенному расчету равной 0,097 м/с при толщине пленки
=0,015 м (для сферических элементов насадки диаметром 30 мм), скорость подъема пузырей согласно [5] равной 2 м/с, скорость жидкости на внешней границе пленки согласно вышеприведенному расчету равной 0,097 м/с при толщине пленки ![]() =0,0001722. Получим
=0,0001722. Получим ![]() ‹ 1, то есть критерий Струхаля является достаточно малой величиной. Пренебрежение этим критерием означает рассмотрение тепловой задачи в квазистационарном приближении.
‹ 1, то есть критерий Струхаля является достаточно малой величиной. Пренебрежение этим критерием означает рассмотрение тепловой задачи в квазистационарном приближении.
Таким образом, течение жидкости в слое пленки можно рассматривать как квазистационарное. Тогда в уравнении движения следует принять ![]() и
и ![]() .
.
Как показали исследования вязкого пристенного слоя [3] градиент давления по оси «у» можно не учитывать. Другими исследованиями [9, 10] была экспериментально доказана независимость коэффициента теплоотдачи от давления в системе в пределах до ![]() . Следовательно, в уравнениях (5) и (6):
. Следовательно, в уравнениях (5) и (6):![]() и
и ![]() .
.
Квазистационарное течение пленочного типа определяется уравнениями, по форме совпадающими с уравнениями ламинарного пограничного слоя. Распределение температур в этом слое также определяется уравнениями в квазистационарном приближении пограничного слоя:
![]() , (9)
, (9)
![]() , (10)
, (10)
![]() . (11)
. (11)
При граничных условиях I рода
у=0; Wх=Wу=0; Т=Тст;
у=![]() ; Wх=Umax; Т=Тср;
; Wх=Umax; Т=Тср; ![]() =
= ![]() .
.
Чтобы выделить критерии, определяющие распределение скоростей и температур в слое пленки, приведем это уравнение к безразмерному виду. За масштаб длин примем ![]() – толщину пленки; за масштаб скорости Umax – скорость на свободной границе пленки и за масштаб температур ∆Т – разность температур на свободной и прилегающей к стенке границах пленки. При этих масштабах:
– толщину пленки; за масштаб скорости Umax – скорость на свободной границе пленки и за масштаб температур ∆Т – разность температур на свободной и прилегающей к стенке границах пленки. При этих масштабах:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
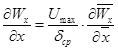 ;
; 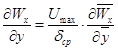 ;
; 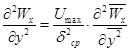 ;
;
![]() ;
; ![]() ;
; 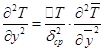 .
.
С учетом этих выражений уравнения (9), (10), (11) в безразмерном виде могут быть записаны как:
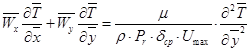 ; (12)
; (12)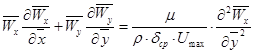 ; (13)
; (13)
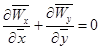 ; (14)
; (14)
Из уравнения (12) следует, что безразмерное значение температуры:
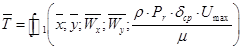 . (15)
. (15)
Из уравнения (13) следует, что безразмерная скорость по окружности трубы теплообменного элемента:
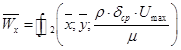 , (16)
, (16)
а безразмерная скорость поперек слоя пленки:
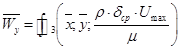 . (17)
. (17)
Из сопоставления (15) и (17) убеждаемся, что безразмерное значение температуры может быть представлено следующим образом:
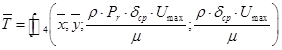 . (18)
. (18)
Как известно [3, 2], тепловой поток при принятых выше масштабах характеризуется локальным критерием:
![]() , (19)
, (19)
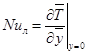 , (20)
, (20)
Тогда, с учетом зависимости (19) будем иметь:
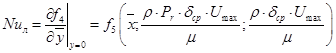 . (21)
. (21)
Так как в конечном итоге нас интересует осредненный коэффициент теплоотдачи по всей поверхности трубы теплообменного элемента, необходимо просуммировать локальные значения критерия ![]() по координате «Х». Это дает:
по координате «Х». Это дает:
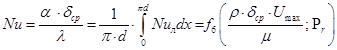 . (22)
. (22)
В критериальном уравнении (22) в качестве определяющей принята скорость на свободной границе пленки. Можно допустить, что эта скорость пропорциональна скорости подъема газовых пузырей в слое орошаемой насадки, и считать:
![]() ; (23)
; (23)
где ![]() – коэффициент пропорциональности.
– коэффициент пропорциональности.
Визуальные наблюдения за характером барботажа показали [10], что погруженный в насадку теплообменный элемент омывают крупные пузыри, подъем которых явно не подчиняется закону Стокса. Движение газовых пузырей в жидкости может быть описано одной из предложенных [6] зависимостей. Однако формулы, описывающие подъем крупных пузырей, содержат в качестве параметра поверхностное натяжение жидкости. А так как исследованиями [9, 10] было установлено отсутствие его влияния на теплоотдачу – эти формулы не могут быть приняты в рассмотрение. Поэтому примем ту зависимость, которая определяет скорость подъема плоских пульсирующих сфероидов [5]. При ![]() она имеет вид:
она имеет вид:
![]() . (24)
. (24)
Умножив числитель и знаменатель на ![]() и подставив в (23), получим:
и подставив в (23), получим:
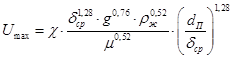 . (25)
. (25)
Введя выражение этой скорости в критерий ![]() уравнения (22), будем иметь:
уравнения (22), будем иметь:
![]() =
= 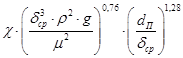 . (26)
. (26)
Таким образом, уравнение (22) приводится к виду:
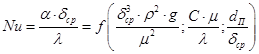 . (27)
. (27)
Осреднение теплового потока по всей поверхности позволяет сделать некоторые логические преобразования в функциональной зависимости (27). При развитом пенном режиме осредненную толщину пленки допустимо считать постоянной, не зависимой от гидродинамики и определяемой только свойствами жидкости. Допущение о независимости толщины пленки от гидродинамики распространимо [3] до струйного режима, наблюдаемого в барботажных аппаратах при очень высоких скоростях газа.
Гипотеза о том, что при пенном режиме барботажа толщина жидкостной пленки определяется только свойствами жидкости, дает право на исключение ![]() из уравнения (27). В этом случае можно не рассматривать симплекс
из уравнения (27). В этом случае можно не рассматривать симплекс ![]() , а при установлении функциональной зависимости между критериями
, а при установлении функциональной зависимости между критериями ![]() и
и ![]() необходимо предусмотреть исключение параметра
необходимо предусмотреть исключение параметра ![]() .
.
Одним из возможных вариантов такой зависимости будет, например, уравнение:
![]() =
= 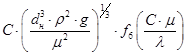 , (28)
, (28)
где ![]() – постоянная величина.
– постоянная величина.
Поскольку уравнение (28) независимо от линейных параметров, для удобства обработки опытных данных в качестве характерного линейного размера в нем можно принять любую величину, например, ![]() – диаметр трубы погружного теплообменного элемента. И тогда это уравнение запишется таким образом:
– диаметр трубы погружного теплообменного элемента. И тогда это уравнение запишется таким образом:
![]() =
=  , (29)
, (29)
или
![]() . (30)
. (30)
Значения ![]() и
и ![]() могут быть установлены только в результате проведения дополнительных экспериментальных исследований.
могут быть установлены только в результате проведения дополнительных экспериментальных исследований.
Так как уравнение (22) дает осреднение локального коэффициента теплоотдачи по окружности трубы погружного теплообменного элемента (по координате Х), уравнение (30) может характеризовать значение ![]() в случае однородности слоя пленки по длине трубы. Это условие будет выдержано при развитом пенном режиме барботажа.
в случае однородности слоя пленки по длине трубы. Это условие будет выдержано при развитом пенном режиме барботажа.
Заключение. Таким образом, на основе проведенного качественного анализа процесса теплоотдачи от наружной поверхности орошаемого рекуперативного теплообменника, погруженного в слой дисперсной насадки, к газожидкостной смеси по аналогии с процессами барботажа получено аналитическое решение критериального уравнения теплообмена. Полученное уравнение описывает теплообмен с учетом характера движения газа со стороны свободной поверхности пленки жидкости. Математическая форма установленных закономерностей позволяет использовать их при расчете теплообменных аппаратов.
Рецензенты:
Манохин В.Я., д.т.н., профессор, профессор кафедры пожарной и промышленной безопасности Воронежского государственного архитектурно-строительного университета, г. Воронеж.
Бараков А.В., д.т.н., профессор, заведующий кафедрой теоретической и промышленной теплоэнергетики Воронежского государственного технического университета, г. Воронеж.



