Ранее приведенными экспериментальными исследованиями [2, 3] установлено, что при воздействии на полимерные клеи, используемые для склеивания изделий из древесины, постоянным электрическим полем в структуре последних происходят существенные преобразования в сторону создания упорядоченных образований из микромолекул. Такие структурные преобразования клея наделяют его способностью создавать клеевые соединения более высокой прочности.
Для практической реализации предлагаемой технологии получения клееной древесины повышенной прочности требуется проведение более глубокого анализа с использованием элементов моделирования. На этапе теоретического исследования поставлена задача по созданию математической модели процесса склеивания древесины клеями марок КФЖ и КФ-МТ-15, обработанных в постоянном электрическом поле. Можно полагать, что модель позволит изучить зависимость прочности клеевого соединения на их основе от параметров технологического процесса и на основе этого оптимизировать этот процесс.
Согласно данным [2, 3] для исследования на микроскопическом уровне сложных систем, к которым можно отнести полимерные клеи, довольно часто используется метод молекулярной динамики [1, 5]. С его помощью моделируются физические свойства твердых тел, жидкостей и газов, а также фазовые превращения при плавлении, кристаллизации, испарении и конденсации. При использовании метода молекулярной динамики каждая микроскопическая частица рассматривается как геометрическое тело простой формы (шар, диск), движущееся в соответствии с законами классической динамики Ньютона и взаимодействующее с другими частицами по определенному закону.
Особенности поведения реальной системы могут быть реализованы в двух измерениях, поэтому для большей наглядности получаемых результатов предлагается двумерная модель. Уход от третьего измерения дает возможность при заданном числе элементов порядка 10000 повысить линейные размеры образца материала в направлениях Х и У. Метилольные группы (мономеры) в модели представлены отдельными круглыми элементами, называемыми в дальнейшем микромолекулами, имеющими три стенки свободы, а именно: движение вдоль осей ОХ и ОУ и вращение вокруг собственной оси.
Каждая в отдельности макромолекула в модели представляет собой электрический диполь с зарядами +q и –q, расположенными на расстоянии d друг от друга. Состояние i-й микромолекулы описывается тремя переменными: декартовыми координатами её центра ![]() и углом поворота
и углом поворота ![]() макромолекулы относительно оси ОХ.
макромолекулы относительно оси ОХ.
В целях формирования начальной конфигурации 10000 кругов – макромолекул случайным образом помещаются в ячейку в форме прямоугольника. На всех границах прямоугольника используются зеркальные граничные условия, когда макромолекула, придя в соприкосновение со стенкой, испытывает абсолютно упругое соударение и возвращается в расчетную ячейку.
Силы взаимодействия между макромолекулами складываются из межмолекулярного взаимодействия, обусловленного отталкиванием электронных оболочек молекул на малых расстояниях и притяжением на больших расстояниях, а также электростатического диполь-дипольного взаимодействия между молекулами.
Отсюда следует, что сила, действующая на i-ю молекулу со стороны всех других молекул данной системы, равняется:
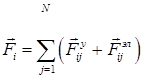 , (1)
, (1)
где ![]() – соответственно силы упругого и электростатического взаимодействия молекул i и j; N – число молекул в модели.
– соответственно силы упругого и электростатического взаимодействия молекул i и j; N – число молекул в модели.
При расчете сил для каждой пары молекул предварительно вычисляется расстояние ![]() между их центрами
между их центрами ![]() и
и ![]() .
.
![]() (2)
(2)
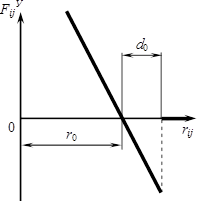
Рис. 1. Зависимость силы упругого взаимодействия двух молекул i и j от расстояния между ними
Первый вид межмолекулярного взаимодействия удобно описать в рамках представления об упругом взаимодействии. Тогда зависимость силы взаимодействия двух молекул i и j от расстояния между ними согласно рис. 1 описывается в виде:
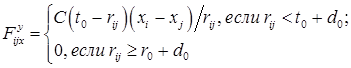 (3)
(3)
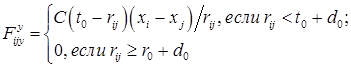
Здесь ![]() и
и ![]() – проекции силы
– проекции силы ![]() на координатные оси ОХ и ОУ соответственно; С – жесткость упругого взаимодействия молекул;
на координатные оси ОХ и ОУ соответственно; С – жесткость упругого взаимодействия молекул; ![]() – диаметр молекулы;
– диаметр молекулы; ![]() – расстояние, на котором молекулы упруго взаимодействуют между собой
– расстояние, на котором молекулы упруго взаимодействуют между собой ![]() .
.
Процесс моделирования осуществляется при участии большого числа молекул и требует значительных затрат времени, поэтому целесообразно оптимизировать алгоритм в направлении снижения времени счета. Для осуществления этой операции применяется следующий прием. Поскольку основной объём вычислений связан с определением сил межмолекулярного взаимодействия, то в процессе расчета сил упругого взаимодействия выдерживается условие
![]() , (4)
, (4)
где ![]() – радиус области, в пределах которой учитывается взаимодействие.
– радиус области, в пределах которой учитывается взаимодействие.
Определение функций ![]() производится при условии выполнения неравенства (4), т. к. в противном случае указанные величины считаются равными нулю. Поскольку на каждом шаге молекулы смещаются на расстояние, значительно меньшее среднего расстояния между ними, то расчет сил можно значительно ускорить, применив следующий прием. Для каждой молекулы составляются массивы с номерами частиц, находящихся на расстояниях, не превышающих
производится при условии выполнения неравенства (4), т. к. в противном случае указанные величины считаются равными нулю. Поскольку на каждом шаге молекулы смещаются на расстояние, значительно меньшее среднего расстояния между ними, то расчет сил можно значительно ускорить, применив следующий прием. Для каждой молекулы составляются массивы с номерами частиц, находящихся на расстояниях, не превышающих ![]() от данной.
от данной.
Для i-й молекулы находится взаимодействие, только с частицами, попавшими в соответствующий массив.
Электростатическое взаимодействие между электрическими зарядами диполей осуществляется по закону Кулона, т.е.
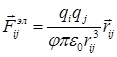 , (5)
, (5)
где ![]() и
и ![]() – электрические заряды в узлах i и j, равные
– электрические заряды в узлах i и j, равные ![]() ;
; ![]() – электрическая постоянная;
– электрическая постоянная; ![]() – радиус-вектор, направленный от заряда i и заряда j.
– радиус-вектор, направленный от заряда i и заряда j.
При приложении влияния электрического поля с напряженностью ![]() на каждый электрический заряд будет действовать дополнительная сила, направленная вдоль поля и описываемая формулой
на каждый электрический заряд будет действовать дополнительная сила, направленная вдоль поля и описываемая формулой
![]() (6)
(6)
Отсюда следует, что на каждый электрический заряд действует сила электростатического взаимодействия:
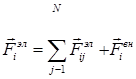 (7)
(7)
На каждую молекулу действует момент силы, вызывающий её вращение относительно центра.
![]() , (8)
, (8)
где ![]() – проекция силы
– проекция силы ![]() на ось ОХ, действующей на заряды
на ось ОХ, действующей на заряды ![]() и
и ![]() соответственно;
соответственно;
![]() – проекции силы
– проекции силы ![]() на ось ОY, действующей на заряды
на ось ОY, действующей на заряды ![]() и
и ![]() соответственно;
соответственно;
d – плечо диполя.
При использовании метода молекулярной динамики численно решаются уравнения движения в форме Ньютона. Для поступательного движения N молекул система уравнений движения имеет вид:
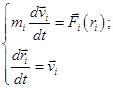 (9)
(9)
Здесь ![]() – масса, скорость и радиус-вектор i-ой молекулы соответственно;
– масса, скорость и радиус-вектор i-ой молекулы соответственно; ![]() – сила, действующая на i-ю молекулу; t – время; i – номер молекулы (i=1, 2, . . ., N).
– сила, действующая на i-ю молекулу; t – время; i – номер молекулы (i=1, 2, . . ., N).
Вращательное движение молекул описывается системой уравнений вида:
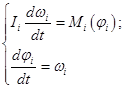 (10)
(10)
В уравнениях (10) ![]() – момент инерции, угловая скорость и угол поворота относительно оси ОХ i-й молекулы;
– момент инерции, угловая скорость и угол поворота относительно оси ОХ i-й молекулы; ![]() – момент силы, действующей на i-ю молекулу.
– момент силы, действующей на i-ю молекулу.
Для численного интегрирования системы уравнений (9) целесообразно применять модифицированный метод Эйлера [ ], т.е.
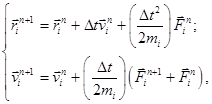 (11)
(11)
где ![]() – шаг интегрирования по времени; n – номер шага интегрирования.
– шаг интегрирования по времени; n – номер шага интегрирования.
Целесообразно в расчетах шаг интегрирования принимать равным ![]()
Система уравнений (10) интегрируется аналогично:
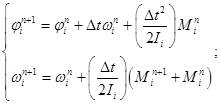 (12)
(12)
Полученный численный алгоритм отмечается простотой, надежностью и устойчивостью, при этом связанная с ним глобальная погрешность имеет третий порядок для координаты и второй порядок для скорости. По сути дела, он является самостартующим и не приводит к накоплению погрешности округления [4].
Для того чтобы в модели корректно учесть влияние температуры отверждения клея, начальное распределение молекул по скоростям задавалось по максвелловскому закону для некоторой температуры ![]() . В целях достижения системой равновесия при заданной температуре необходимо произвести корректировку скоростей на каждом временном шаге по формуле:
. В целях достижения системой равновесия при заданной температуре необходимо произвести корректировку скоростей на каждом временном шаге по формуле:
![]() (13)
(13)
где ![]() – нормированный множитель изображается в виде:
– нормированный множитель изображается в виде:
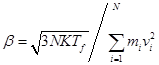 (14)
(14)
Здесь К – постоянная Баумана.
На каждом шаге по времени осуществлялся контроль над потенциальной энергией системы W, т.е.
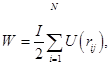 (15)
(15)
где ![]() – потенциальная энергия взаимодействия молекул i и j.
– потенциальная энергия взаимодействия молекул i и j.
Процедура интегрирования уравнений движения по формулам (10) и (11) продолжалась до тех пор, пока значение потенциальной энергии системы уменьшалось. Для достижения системой равновесия требовалось около 20000 временных шагов, после чего величина W начинала осциллировать относительно равновесного значения.
Как видно выше, предположенная модель представляет собой систему дифференциальных и алгебраических уравнений. Для удобства исследования системы уравнений составлена компьютерная программа «Программа для моделирования процесса склеивания древесины клеями КФ, обработанными в электрическом поле» на языке Object Pascal в интегрированной среде программирования Borland Delphi 7.0.
В процессе компьютерного эксперимента на экран компьютера непрерывно выводятся следующие выходные характеристики.
Схематическое изображение области клея прямоугольной формы и поверхности древесины, по которым можно визуально анализировать происходящие в клее процессы и оценивать эффективность склеивания.
Зависимость степени поляризации ![]() от времени и зависимость количества клеевых связей
от времени и зависимость количества клеевых связей ![]() от времени.
от времени.
Диаграмма взаимного углового распределения соседних молекул Р(![]() ) в декартовом и полярном видах.
) в декартовом и полярном видах.
В процессе реализации математической модели проведена серия компьютерных экспериментов. Так, исследовано влияние напряженности электрического поля на прочность склеивания древесины. Установлено, что воздействие на клей электрическим полем способствует упорядочению диполей. Существующие в клее ограниченные области сонаправленных диполей начинают укрупняться и выстраиваться вдоль поля. В рамках изучаемой серии изменяли значение напряженности поля Е от 0 до 1200 В/см с шагом 150 В/см. Полученные данные приведены в виде графика на рис. 2.
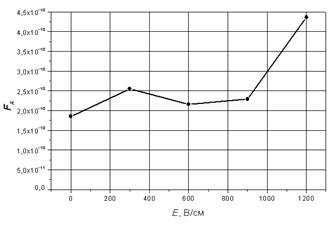
Рис. 2. Зависимость силы адгезии FА клея КФЖ к поверхности древесины дуба от напряженности электрического поля Е
Как видно из рис. 2, увеличение напряженности электрического поля приводит к росту сил адгезии.
Подобным способом исследовалось влияние времени выдержки клея в электрическом поле на адгезионную прочность клеевого соединения древесины. Принято, что напряженность электрического поля составляла 1200 В/см. Полученные в процессе компьютерного эксперимента данные, представленные на рис. 3, свидетельствуют о том, что максимальное значение силы адгезии под действием электрического поля достигается на 700 шаге, что составляет по времени примерно 12 мин.
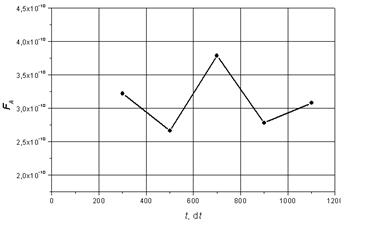
Рис. 3. Зависимость силы адгезии FА клея КФЖ к поверхности древесины дуба от времени t выдержки клея в электрическом поле
В заключение следует отметить, что предлагаемая модель процесса модифицирования клеев путем воздействия электрическим полем позволяет получать информацию по значениям основных факторов, оказывающих влияние на создание клеевых соединений древесины повышенной прочности.
Применение данной модели расширяет возможности технологического воздействия на процесс склеивания древесины.
Рецензенты:
Никулин С.С., д.т.н., профессор, профессор кафедры технологии органического синтеза и высокомолекулярных соединений ФГБОУ ВПО «Воронежский государственный университет инженерных технологий», г. Воронеж.
Филимонова О.Н., д.т.н., профессор, профессор кафедры инженерной экологии ФГБОУ ВПО «Воронежский государственный университет инженерных технологий», г. Воронеж.



