Введение
По аналогии с определением бинарной случайной среды, приведенным в [4], случайная среда (однородный процесс с независимыми приращениями в терминологии [5]) с нормально распределенными доходами – это управляемый случайный процесс 
, значения которого интерпретируются как доходы, зависящие только от выбираемых в текущие моменты времени действий и имеющие нормальные распределения с плотностями
, (1)
если 
. При такой постановке задачи случайная среда описывается вектором математических ожиданий 
. В данном случае параметр фиксирован, но неизвестен лицу, осуществляющему управление.
Постановка задачи
Введем целевую функцию потерь 
, значениями которой являются потери за время моделирования, где 
– используемая стратегия. Если параметр 
известен, то наилучшей стратегией является та, которая применяет только то действие, которому соответствует большая из величин 
, и максимальный полный доход в этом случае равен 
. Если же неизвестен, то неизбежно возникают потери вследствие неполноты информации о среде, равные:
. (2)
Здесь 
представляет собой математическое ожидание потерь полного дохода. Предполагается, что ограничения на множество допустимых значений параметра имеют следующий вид:
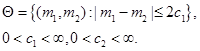(3)
При использовании минимаксного подхода, предложенного, например, в [2], цель управления состоит в минимизации величины потерь полного дохода на множестве параметров 
по множеству стратегий 
. При этом минимаксный риск 
выглядит следующим образом:
. (4)
Для реализации этой цели предлагается использовать пороговую стратегию, предложенную в [6].
Стратегия управления с одним порогом
Итак, рассмотрим пороговую стратегию . Она применяет действия 
и 
среды по очереди, накапливая доходы 
и 
соответственно. На каждом шаге вычисляется абсолютная разность доходов на действиях 
. Действия применяются до тех пор, пока эта величина не превысит порога 
, где 
– полное время управления, 
– пороговая константа, или не истечет время управления. Если время управления не истекло, то действие, которому соответствует меньшая величина набранного дохода, исключается из рассмотрения, а оставшееся время применяется только другое действие.
Можно показать, что наибольшие потери полного дохода будут иметь место при
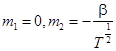. (5)
На основе пороговой стратегии , рассмотренной выше, была разработана программа. Прежде сделаем замечание. Целевая функция потерь , вообще говоря, зависит от параметров и . Но для расчетов нам удобнее полагать, что она зависит от и 
, где – пороговая константа, использующаяся пороговой стратегией, – параметр среды.
Итак, алгоритм работы программы построен таким образом, что в ней для каждой пары 
вычисляется средний доход 
, где 
– доход за одно моделирование, 
– количество моделирований. Затем вычисляются средние потери математического ожидания дохода 
. После этого при каждой константе определяются минимальные потери 
. При каждой константе подбираются максимальные потери 
. Точка, в которой 
, является минимаксной точкой, в которой достигается минимальная гарантированная величина потерь полного дохода.
В результате вычислений оптимальное значение 
оказалось равным 
, при этом максимальные потери 
соответствуют 
. Время моделирования выбиралось из условия 
, количество моделирований 
, что позволяет говорить о точности вычислений 
[1]. Анализируя полученные результаты, видно, что параметры случайной среды с нормально распределенными доходами идентичны параметрам бинарной случайной среды [4], а потери примерно в 2 раза выше. Это соответствует теории.
Таблица 1 показывает результаты итоговых вычислений. Все потери в таблице являются приведенными путем деления на 
. Желтым цветом обозначены локальные минимумы по для каждого , зеленым – локальные максимумы по для каждого , сиреневым – точка, в которой минимум по равен максимуму по .
Таблица 1 – Значения 
|
|
0,43 |
0,46 |
0,49 |
0,52 |
0,55 |
0,58 |
0,61 |
0,64 |
0,67 |
0,7 |
|
2,0 |
0,652 |
0,645 |
0,639 |
0,637 |
0,634 |
0,637 |
0,638 |
0,641 |
0,644 |
0,651 |
|
2,5 |
0,721 |
0,713 |
0,706 |
0,702 |
0,698 |
0,700 |
0,704 |
0,709 |
0,713 |
0,720 |
|
3,0 |
0,766 |
0,756 |
0,744 |
0,740 |
0,738 |
0,739 |
0,743 |
0,749 |
0,756 |
0,767 |
|
3,5 |
0,788 |
0,774 |
0,764 |
0,758 |
0,756 |
0,761 |
0,764 |
0,772 |
0,783 |
0,793 |
|
4,0 |
0,793 |
0,779 |
0,766 |
0,762 |
0,761 |
0,765 |
0,771 |
0,782 |
0,794 |
0,806 |
|
4,5 |
0,787 |
0,772 |
0,762 |
0,758 |
0,758 |
0,760 |
0,770 |
0,781 |
0,796 |
0,812 |
|
5,0 |
0,775 |
0,758 |
0,749 |
0,745 |
0,748 |
0,755 |
0,764 |
0,777 |
0,795 |
0,811 |
|
5,5 |
0,756 |
0,740 |
0,735 |
0,731 |
0,735 |
0,741 |
0,754 |
0,769 |
0,788 |
0,807 |
|
6,0 |
0,733 |
0,721 |
0,714 |
0,715 |
0,722 |
0,731 |
0,745 |
0,761 |
0,781 |
0,803 |
|
6,5 |
0,710 |
0,702 |
0,697 |
0,700 |
0,708 |
0,717 |
0,736 |
0,755 |
0,775 |
0,797 |
Двухпороговая стратегия управления
Рассмотрим теперь потери на множестве допустимых параметров для следующих двух случаев. На диаграмме линия 1 показывает минимальные потери для минимальных для каждого , линия 2 – потери для фиксированного 
(все потери также являются приведенными).
Как нетрудно заметить, начиная с 
и до 
потери за моделирование практически идентичны. После этого потери для случая с фиксированным увеличиваются и в определенный момент устанавливаются на величине порога 
. Очевидно, это связано с тем, что при больших значениях параметра лучшее действие определяется достаточно быстро (так как, например, при 
математические ожидания на действиях различаются значительно, 
), но большое значение пороговой константы (при порог 
) требует значительного времени на достижение этого порога. Этот недостаток стратегии можно устранить, если ввести дополнительный порог 
, с помощью которого при больших оптимальное действие будет определяться быстрее. В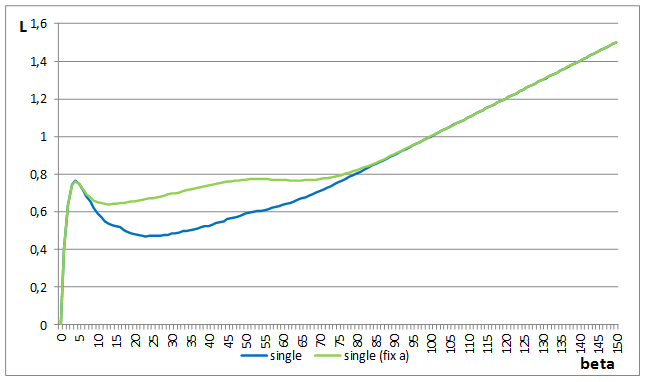 
Рисунок 1 – Графики значений функции потерь на множестве значений 
. Линия 1 показывает потери при минимальных 
для каждого , линия 2 – потери для фиксированного 
.
этом случае стратегия будет выглядеть следующим образом. Начиная с некоторого времени 
текущий порог 
заменяется на , после чего моделирование продолжается в обычном порядке.
Очевидно, что теперь при высоких значениях неоптимальное действие будет в среднем исключаться из рассмотрения быстрее. Введем новую величину 
, которая будет показывать суммарные потери на всём множестве . Рассматривание данной величины вполне уместно, так как можно считать, что значения множества распределены равномерно.
Расчет значений
Итак, рассчитаем значения 
для приведенных выше данных. Более конкретно, нас интересуют следующие значения: 
– для первого случая, 
– для случая фиксированного и 
– для случая двойного порога. Вычисления показывают, что 
, 
. Далее был проведен полный расчет значений суммарных потерь за время моделирования при , , , 
, 
, 
. Искались такие параметры и 
, при которых будет наименьшим, при этом ни одно из значений потерь не превышает вычисленной величины гарантированных потерь полного дохода 
. В итоге удалось достигнуть значения 
при 
, 
. Диаграмма это демонстрирует, потери при таких параметрах обозначены на диаграмме:
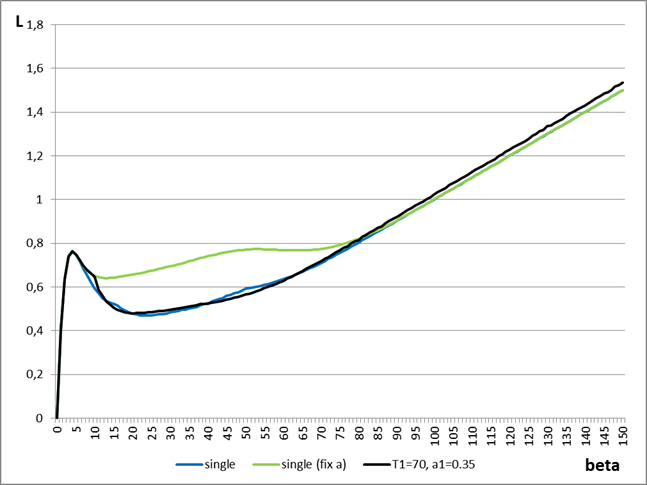
Рисунок 2 – Графики значений функции потерь на множестве значений . Линия 1 показывает потери при минимальных для каждого , линия 2 – потери для фиксированного , линия 3 – потери при фиксированном , 
, 
.
Это позволяет судить о том, что введение дополнительного порога позволяет уменьшить потери на 22% по сравнению с фиксированным , делая их сравнимыми с потерями первого случая.
Заключение
Итак, рассмотрена пороговая стратегия управления в случайной среде с нормально распределенными доходами с двумя действиями. Найдены оптимальные значения пороговой константы и параметра среды. Также рассмотрены суммарные потери дохода на множестве допустимых параметров среды и показано, что их можно значительно снизить с помощью введения дополнительного порога.
Автор благодарит профессора А.В. Колногорова за помощь в постановке задачи и обсуждение полученных результатов.
Рецензенты:
Кирьянов Б.Ф., д.т.н., профессор, ФГБОУ ВПО «Новгородский государственный университет имени Ярослава Мудрого», г. Великий Новгород.
Едемский В.А., д.ф.-м.н., профессор кафедры ПМИ, ФГБОУ ВПО «Новгородский государственный университет имени Ярослава Мудрого», г. Великий Новгород.