Введение
Перед производителями ставится задача – повысить энергетические характеристики постоянных магнитов (ПМ). Причем данная задача направлена не только на методы количественного поиска (повышение удельной энергии, остаточной индукции и коэрцитивной силы), результаты которого зависят от свойств намагничиваемого материала, но и на качественный, в частности, это повышение однородности магнитного поля ПМ, которая зависит от характеристик намагничивающей установки (НУ) для производства ПМ [2].
Для повышения однородности поля ПМ авторами разработана оригинальная конструкция НУ (заявка на выдачу патента на изобретение №2013101279), рисунок 1, которая содержит электромагнит, выполненный в виде n–полюсного сердечника 1 с обмотками 2, соединенными электрически с источником импульсного тока 3, намагничиваемый элемент (НЭ) 4, установленный на сердечнике 5, на котором намотаны дополнительные обмотки 6. Представленная конструкция отличается от известных [1,4] введением дополнительных обмоток, задачей которых является усиление магнитного потока электромагнита.
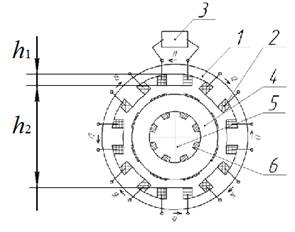
Рисунок 1. Расчетная схема предлагаемого технического решения НУ
Анализ данных моделирования, проведенный в [4], показал: при применении дополнительных обмоток намагничиваемый элемент промагничивается полностью и однородно, что подтверждает перспективность внедрения на практике предлагаемого технического решения, для чего необходимо разработать математическую модель НУ.
При решении данной задачи рассматривается расчетная схема НУ, рисунок 1.
При этом ввиду сложности расчетов используются обычные при решении такого класса задач допущения:
1. Радиусы кривизны магнитопровода значительно больше зазора.
2. Магнитная проницаемость немагнитного зазора равна проницаемости вакуума ![]() , магнитная проницаемость стали сердечника равна бесконечности
, магнитная проницаемость стали сердечника равна бесконечности![]() .
.
В качестве источника питания обмоток НУ используется блок конденсаторов, рисунок 2, тогда ток основной и дополнительной обмотки можно представить в виде [5]:
![]() (1)
(1)
где U – напряжение сети; t – минимальная продолжительность намагничивающего импульса; L – общая индуктивность контура; w' – угловая частота колебаний; b=R/2L; R – полное активное сопротивление цепи.
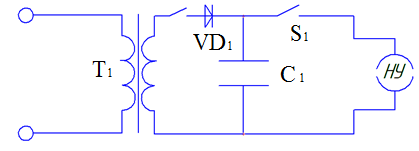
Рисунок 2. Схема питания обмоток НУ
Общая индуктивность контура может быть представлена суммой индуктивностей обмоток (НУ). В виду нелинейности материалов, применяемых в НУ, аналитический расчет индуктивности является затруднительным, в связи с чем представляется целесообразным определить индуктивности основной и дополнительной обмотки численными методами.
Для этого в работе используется метод конечных элементов, реализуемый в программном комплексе AnsysMaxwell. При этом решается двумерная задача анализа электромагнитного поля, на конечно-элементной модели разработанной по расчетной схеме, рисунок 1.
Определим магнитный поток НУ:
![]() (2)
(2)
![]() (3)
(3)
где ![]() – магнитный поток;
– магнитный поток; ![]() – полное магнитное сопротивление цепи. В то же время МДС:
– полное магнитное сопротивление цепи. В то же время МДС:
![]() (4)
(4)
где ![]() – магнитодвижущая сила; i – максимальный ток; w – число витков на полюс.
– магнитодвижущая сила; i – максимальный ток; w – число витков на полюс.
Для определения магнитного сопротивления НУ разбивается на участки: магнитопровод, воздушный зазор, намагничиваемый элемент.
![]() (5)
(5)
где ![]() – общее магнитное сопротивление зазора;
– общее магнитное сопротивление зазора;![]() – магнитное сопротивление намагничивающего элемента;
– магнитное сопротивление намагничивающего элемента;![]() – магнитное сопротивление магнитопровода; n, k – количество участков в магнитопроводе и намагничивающем элементе, соответственно.
– магнитное сопротивление магнитопровода; n, k – количество участков в магнитопроводе и намагничивающем элементе, соответственно.
Потокосцепление обмоток НУ:
![]() (6)
(6)
C учетом (2), (3) и (4), (6) индуктивность основной обмотки определяется выражением:
![]() (7)
(7)
При компьютерном моделировании определялась индуктивность основной обмотки. С учетом выражений (2–7) и данных моделирования, на рисунке 3 представлена зависимость
индуктивности основной обмотки от тока.
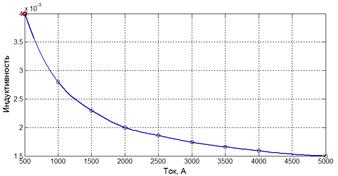
Рисунок 3. Зависимость индуктивности основной обмотки от силы тока
Из анализа рисунка 3 видно, что с увеличением тока в 3 раза индуктивность в основной обмотке уменьшается на 39,28 %, а при увеличении тока в 5 раз уменьшается на 46,42 %.
Аналогичным образом определяется индуктивность дополнительной обмотки.
Расчётная величина b, представленная в выражении (8), зависит от способа соединения обмоток, поэтому рассматривается 2 варианта соединения основной и дополнительной обмотки.
При последовательном соединении обмоток, b определяется в виде:
![]() (8)
(8)
где ![]() и
и ![]() – индуктивности основной и дополнительной обмоток НУ соответственно;
– индуктивности основной и дополнительной обмоток НУ соответственно; ![]() и
и ![]() – активное сопротивление обмоток.
– активное сопротивление обмоток.
При параллельном соединении b будет представлена в виде:
![]() (9)
(9)
Исходя из результатов моделирования, закон полного тока для рассматриваемой конструкционной схемы представляется в виде:
![]() (10)
(10)
где i – сила тока в основной и дополнительной обмотке;![]() – число витков основной и дополнительной обмотки;
– число витков основной и дополнительной обмотки;![]() – напряженность в магнитопроводе намагничивающей установки;
– напряженность в магнитопроводе намагничивающей установки; ![]() – напряженность в воздушном зазоре;
– напряженность в воздушном зазоре; ![]() – напряженность в намагничиваемом элементе;
– напряженность в намагничиваемом элементе;![]() – напряженность в сердечнике, на котором установлен намагничиваемый элемент;
– напряженность в сердечнике, на котором установлен намагничиваемый элемент; ![]() – напряженность магнитного поля создаваемого дополнительной обмоткой;
– напряженность магнитного поля создаваемого дополнительной обмоткой; ![]() – величина воздушного зазора;
– величина воздушного зазора;![]() – толщина НЭ;
– толщина НЭ; ![]() – максимальная глубина проникновения магнитного поля в магнитную систему НУ;
– максимальная глубина проникновения магнитного поля в магнитную систему НУ; ![]() – осевая длина магнитопровода НУ.
– осевая длина магнитопровода НУ.
При этом глубина проникновения магнитного поля в магнитную систему НУ:
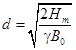 , (11)
, (11)
где ![]() – необходимая напряженность на данной глубине;
– необходимая напряженность на данной глубине; ![]() – удельная проводимость материала магнита;
– удельная проводимость материала магнита; ![]() – плотность магнитного потока на данной глубине в теле НЭ.
– плотность магнитного потока на данной глубине в теле НЭ.
Представляя напряженность и остаточную индукцию как функции магнитной проницаемости НЭ (11), максимальная глубина проникновения определяется в виде:
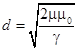 , (12)
, (12)
С учетом (12):
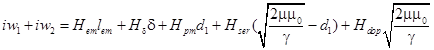 , (13)
, (13)
Таким образом, выражение (13) является выражением, описывающим процесс намагничивания постоянного магнита.
Основным элементом НУ является электромагнит, уравнение принимается в виде:
![]() , (14)
, (14)
При разработке математического аппарата, позволяющего проектирование НУ, необходимо ввести ряд ограничений, вызванных природой физических процессов, протекающих в ней. К таким ограничениям относятся тепловые и электромагнитные.
Тепловые ограничения определяются тем, что для намагничивания высокоэнергетических постоянных магнитов необходим значительный по величине импульс тока. В связи с этим время действия данного импульса ограниченно теплостойкостью обмоток, а также точкой Кюри изготавливаемого постоянного магнита:
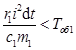 , (15)
, (15)
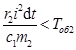 , (16)
, (16)
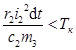 , (17)
, (17)
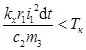 , (18)
, (18)
где ![]() ,
,![]() – удельная теплоемкость материалов обмотки и НЭ, соответственно;
– удельная теплоемкость материалов обмотки и НЭ, соответственно; ![]() ,
, ![]() – масса основной и дополнительной обмотки,
– масса основной и дополнительной обмотки, ![]() – масса НЭ;
– масса НЭ; ![]() – эмпирический коэффициент.
– эмпирический коэффициент.
Электромагнитные ограничения определяются кривой намагничивания магнитопровода:
![]() , (19)
, (19)
где ![]() – напряженность в сердечнике электромагнита НУ;
– напряженность в сердечнике электромагнита НУ; ![]() – максимально-допустимое значение напряженности, ограниченное температурой Кюри.
– максимально-допустимое значение напряженности, ограниченное температурой Кюри.
Воспользуемся известным выражением для определения времени действия импульса [6]:
![]() , (20)
, (20)
где ![]() – минимальная продолжительность намагничивающего импульса; D – эффективный диаметр ПМ;
– минимальная продолжительность намагничивающего импульса; D – эффективный диаметр ПМ;![]() – удельная проводимость НЭ;
– удельная проводимость НЭ;![]() – напряженность намагничивающего поля.
– напряженность намагничивающего поля.
С учетом принятых допущений и определенных выше физических ограничений определяется математическая модель намагничиваемой установки:
 (21)
(21)
Решение системы (21) аналитическими способами является весьма затруднительной задачей. В связи с этим для анализа динамических и статических процессов в НУ целесообразно применение имитационного моделирования в пакете MatlabSimulink.
При математическом моделировании, с учетом принятых допущений, кривая намагничивания стали сердечника и магнитопровода НУ описывается уравнением [2]:
![]() . (22)
. (22)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() – эмпирические коэффициенты.
– эмпирические коэффициенты.
Имитационная модель, рисунок 4, представляет собой реализацию уравнения закона полного тока. Каждая отдельная ветвь представляет собой напряженность определенного участка магнитной цепи НУ. Верхняя ветвь представляет собой напряженность магнитного
поля основной обмотки.
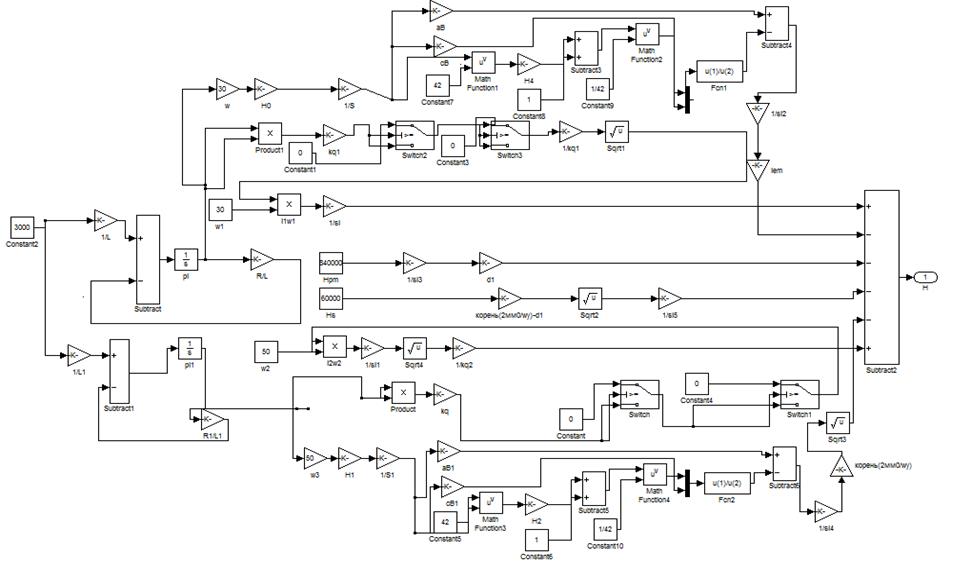
Рисунок 4. Модель намагничивающей установки
С помощью данной модели можно изучать статические и динамические режимы работы намагничивающей установки. Анализ результатов моделирования показал их соответствие реальным физическим процессам.
Полученный результат может быть использован на практике при проектировании намагничивающих установок.
Рецензенты:
Ураксеев М.А., д.т.н., профессор кафедры информационно-измерительных систем ФГБОУ ВПО «Уфимский государственный авиационный технический университет», г. Уфа.
Демин А.Ю., д.т.н., профессор кафедры электроники и биомедицинских технологий ФГБОУ ВПО «Уфимский государственный авиационный технический университет», г. Уфа.



