Введение и постановка задачи.Технологический процесс изготовления сварных соединений неизбежно связан с возникновением в области сварного шва границ сплавления, зоны термического влияния химической, структурной и в конечном счете механической неоднородности. При этом соединение можно представить состоящим из участков металла, имеющего различные прочностные и пластические свойства, обладающего разной трещиностойкостью и т.д. Наибольший интерес с точки зрения работоспособности при различных видах нагружения вызывают сварные соединения, ослабленные мягкими прослойками (участками), которые лимитируют прочностные и пластические свойства сварных соединений в целом.В работе [3] в случае растяжения (сжатия) данных соединений предложены расчетные зависимости для определения их предельной несущей способности. Однако в ряде случаев сварные соединения с мягкими прослойками испытывают изгиб. В этой связи настоящая работа посвящена изучению предельной несущей способности рассматриваемых соединений, работающих в условиях статического изгиба.
Решение поставленной задачи.Для решения поставленной задачи был выполнен анализ предельного состояния соединений с мягкой прослойкой при изгибе (рис.1). Для этого применяли метод конечных элементов -МКЭ (Программный комплекс ANSYS[1]), базирующийся на теории пластического течения[2]. Для построения конечно-элементных сетокиспользовали прямоугольные элементы с размерами сторон от 0,1В(вдали от контактных границ прослойки) до 0,01В(в области сварного шва). ЗдесьВ – толщина сварного соединения.
Допущения,принимаемые при анализе, были аналогичными
работе [3]. Рассматриваемые в численных расчетах модели сварных соединений с
мягкой прослойкой нагружали по схеме чистого изгиба до предельного состояния.
Степень механической неоднородности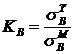 (отношение временного сопротивления твердого,
основного металла
(отношение временного сопротивления твердого,
основного металла![]() к аналогичной характеристике металла мягкой прослойки
к аналогичной характеристике металла мягкой прослойки![]() ) варьировали от 1 до 5, а
относительную толщину прослойки
) варьировали от 1 до 5, а
относительную толщину прослойки ![]() от 0,1…0,7, где h - толщина мягкой прослойки
(рис.1,обозначения). На основе расчетов МКЭ строили поля пластических
перемещений, а также определяли компоненты нормальных и касательных напряжений
в области пластического течения в условиях плоской деформации.
от 0,1…0,7, где h - толщина мягкой прослойки
(рис.1,обозначения). На основе расчетов МКЭ строили поля пластических
перемещений, а также определяли компоненты нормальных и касательных напряжений
в области пластического течения в условиях плоской деформации.
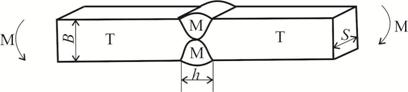
Рис. 1. Модель сварного соединения с мягкой прослойкой при изгибе
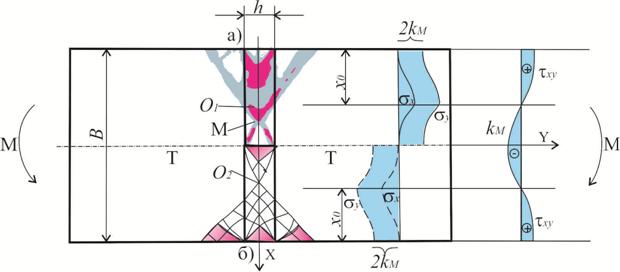
Рис. 2. Картина пластических перемещений с эпюрами напряжений τхуна контакте металлов М и Т , а также эпюры нормальных напряженийσхи σу по центральному сечению мягкой прослойки (МКЭ) (верхняя часть рисунка - а) и соответствующая данной картине сетка линий скольжения с аналогичными эпюрами напряжений (нижняя часть рисунка -б)
На рис.
2 в качестве примера представлена картина пластического течения и эпюры
напряжений ![]() вдоль
контактной границы мягкой прослойки и твердого (основного) металла, а также
распределение нормальных напряжений
вдоль
контактной границы мягкой прослойки и твердого (основного) металла, а также
распределение нормальных напряжений ![]() и
и ![]() по центральному сечению мягкой прослойки для
соединения с
по центральному сечению мягкой прослойки для
соединения с ![]() и
и
![]() . В верхней
части рисунка (рис.2а) представлены данные, полученные методом МКЭ, а в нижней
(рис.2б) – результаты теоретического построения сеток линий скольжения,
соответствующие пластическому деформированию сварного соединения. Сетки линий
скольжения построены по закономерностям, изложенным в работе [3]. Отметим, что
картина пластического течения и построенных сеток линий скольжения обладает
симметрией относительно оси Y (центральной оси) и
вследствие этого приведена как совмещенная.
. В верхней
части рисунка (рис.2а) представлены данные, полученные методом МКЭ, а в нижней
(рис.2б) – результаты теоретического построения сеток линий скольжения,
соответствующие пластическому деформированию сварного соединения. Сетки линий
скольжения построены по закономерностям, изложенным в работе [3]. Отметим, что
картина пластического течения и построенных сеток линий скольжения обладает
симметрией относительно оси Y (центральной оси) и
вследствие этого приведена как совмещенная.
Анализ полученных данных показал, что механизм
контактного упрочнения мягкой прослойки при растяжении (сжатии) и изгибе во
многом совпадает. Однако при изгибе был выявлен ряд особенностей, имеющих
принципиальное отличие от растяжения. В частности, при изгибе имеют место две
линии разветвления пластического течения мягкой прослойки. Они расположены
симметрично относительно оси Y в зоне растяжения и в зоне
сжатия и представлены соответственно точками О1
и О2
на оси Х. По аналогии с растяжением (сжатием) местоположение данных точек
совпадает с точками максимальных значений ![]() и
и ![]() и определяет места смены знака касательных
напряжений
и определяет места смены знака касательных
напряжений ![]() ,
действующих на контактной поверхности мягкой прослойки. Точки разветвления
пластического течения делят мягкую прослойку на две характерные области
напряженно-деформированного состояния. На участке О1О2 (область
№1) практически при любых значениях
,
действующих на контактной поверхности мягкой прослойки. Точки разветвления
пластического течения делят мягкую прослойку на две характерные области
напряженно-деформированного состояния. На участке О1О2 (область
№1) практически при любых значениях ![]() наблюдается локализация пластических деформаций
в мягкой прослойке.При этом касательные напряжения
наблюдается локализация пластических деформаций
в мягкой прослойке.При этом касательные напряжения ![]() определяются параметром χ и принимают значения от
0 в точках О1 и О2 до
определяются параметром χ и принимают значения от
0 в точках О1 и О2 до ![]() на середине контактных
границ мягкого и твердого металла. Для тонких прослоек с
на середине контактных
границ мягкого и твердого металла. Для тонких прослоек с ![]() , когда «пластический шарнир» в
центральной части мягкой прослойки касается контактных границ мягкого и
твердого металлов
, когда «пластический шарнир» в
центральной части мягкой прослойки касается контактных границ мягкого и
твердого металлов ![]() ,где
,где
![]() –
предел текучести на сдвиг мягкого металла М.
В рассматриваемой области, как показали данные МКЭ, отсутствует вовлечение
основного металла в пластическую деформацию практически при любой степени
механической неоднородности. В остальной части мягкой прослойки от точек О1
и О2 до боковых
поверхностей сварного соединения (область 2, характеризующая зону растяжения и зону
сжатия – отрезок хона
рис.2) касательные напряжения на контакте мягкого (
–
предел текучести на сдвиг мягкого металла М.
В рассматриваемой области, как показали данные МКЭ, отсутствует вовлечение
основного металла в пластическую деформацию практически при любой степени
механической неоднородности. В остальной части мягкой прослойки от точек О1
и О2 до боковых
поверхностей сварного соединения (область 2, характеризующая зону растяжения и зону
сжатия – отрезок хона
рис.2) касательные напряжения на контакте мягкого (![]() ) и твердого (
) и твердого (![]() ) металлов определяются параметром
) металлов определяются параметром ![]() и с погрешностью до 5% (по
сравнению МКЭ) аппроксимируются выражением, которое было получено для случая
растяжению (сжатия) сварного соединения [3]:
и с погрешностью до 5% (по
сравнению МКЭ) аппроксимируются выражением, которое было получено для случая
растяжению (сжатия) сварного соединения [3]:
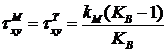 . (1)
. (1)
При построении сеток линий скольжения
по аналогии с работой [3] учитывали особенности их преломления при переходе
через границу металлов М иТ, вызванные условием неразрывности
касательных![]() и нормальных
и нормальных ![]() напряжений. В зоне 1 (между точками
разветвления пластического течения О1 О2
, где основной металлТ не
вовлекается в пластическую деформацию) сетки линий скольжения
представлены семейством циклоид с радиусом производящего круга
напряжений. В зоне 1 (между точками
разветвления пластического течения О1 О2
, где основной металлТ не
вовлекается в пластическую деформацию) сетки линий скольжения
представлены семейством циклоид с радиусом производящего круга ![]() (рис.2б).
(рис.2б).
По аналогии с работой [1] сетки линий
скольжения в области 2 (в зоне растяжения и в зоне сжатия) для учета вовлечения
в пластическую деформацию основного металла были представлены в мягкой прослойке
семейством циклоид с радиусом производящего круга 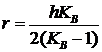 .
.
Используя свойства линий скольжения,были
получены выражения для определения нормальных напряжений σупо
центральному сечению мягкой прослойки в зависимости от ее геометрических
параметров и степени механической неоднородности. В области 1 (между точками
разветвления пластического теченияО1О2)
для зоны растяжения для участка ![]() :
:
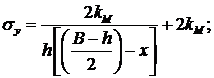 (2)
(2)
при![]() :
:
![]() .(3)
.(3)
Для зоны сжатия для участка ![]() :
:
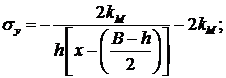 (4)
(4)
при![]() :
:
![]() . (5)
. (5)
Здесь хо - координата точек разветвления течения О1и О2 (рис.2).
Выражения
для определения напряжений ![]() по центральному сечению мягкой прослойки выше и ниже
точек разветвления пластического сечения для зоны растяжения на участке
по центральному сечению мягкой прослойки выше и ниже
точек разветвления пластического сечения для зоны растяжения на участке ![]() :
:
![]() ; (6)
; (6)
при
![]() :
:
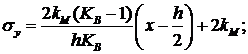 (7)
(7)
для
зоны сжатия для участка ![]() :
:
![]() ; (8)
; (8)
при![]() :
:
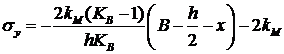 . (9)
. (9)
Полученные компоненты напряженного состояния мягкой прослойки с погрешностью до 10% совпадают с данными работы [5], в которой напряженное состояние сварных соединений при изгибе оценивалось на основе метода муаровых полос.
Для определения несущей способности
сварных соединений с мягкой прослойкой при изгибе определяли величину
предельного изгибающего момента ![]() . Для определения данной величины
использовали условие статической эквивалентности напряжений
. Для определения данной величины
использовали условие статической эквивалентности напряжений ![]() и
внешнихусилий
по изгибающему моменту:
и
внешнихусилий
по изгибающему моменту:
![]() ,
(10)
,
(10)
где S– ширина сварного соединения (рис.1).
При этом с учетом выражений (2-10) получаем:
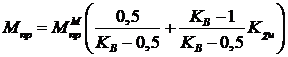 ; (11)
; (11)
где![]() - коэффициент контактного упрочнения мягкой прослойки
при статическом изгибе:
- коэффициент контактного упрочнения мягкой прослойки
при статическом изгибе: 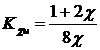 ;
;![]() – предельный изгибающий момент для
пластины из металла М тех же
размеров, что и рассматриваемое сварное соединение:
– предельный изгибающий момент для
пластины из металла М тех же
размеров, что и рассматриваемое сварное соединение:![]() .
.
Заменяя идеально упругопластическую
диаграмму модели на реальные диаграммы деформирования материалов с учетом
аппроксимации участка идеальной пластичности на уровень значений временного
сопротивления мягкого ![]() и твердого металлов
и твердого металлов![]() и
используя условие пластичности Губера-Мизеса(
и
используя условие пластичности Губера-Мизеса(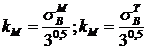 ),оценивали
предельный изгибающий моментсварного соединения с учетом временного
сопротивления мягкого и твердого металлов и его геометрических характеристик.
),оценивали
предельный изгибающий моментсварного соединения с учетом временного
сопротивления мягкого и твердого металлов и его геометрических характеристик.
Анализ
полученного решения (11) показывает, что эффект контактного упрочнения при
изгибе имеет место в диапазоне следующих значений относительных толщин мягких
прослоек:![]() . При достижении значений
. При достижении значений 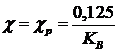 предельный изгибающий момент достигает значений
предельного изгибающего момента для пластины из твердого «Т» металла. При этом
предельный изгибающий момент достигает значений
предельного изгибающего момента для пластины из твердого «Т» металла. При этом  и при
и при![]() данное значение
данное значение ![]() остается постоянным. Если относительная толщина
мягкой прослойки становится равной
остается постоянным. Если относительная толщина
мягкой прослойки становится равной ![]() , то предельный изгибающий
момент сварного соединения соответствует значениям, характерным для предельного
изгибающего момента пластины из мягкого «М»
металла
, то предельный изгибающий
момент сварного соединения соответствует значениям, характерным для предельного
изгибающего момента пластины из мягкого «М»
металла 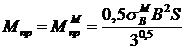 . При
. При![]() значение
значение ![]() остается постоянным. Таким образом,
величина предельного изгибающего момента для соединений с мягкой прослойкой в
зависимости от ее относительной толщины и степени механической неоднородности
изменяется в достаточно широких пределах. Однако расчетная величина
остается постоянным. Таким образом,
величина предельного изгибающего момента для соединений с мягкой прослойкой в
зависимости от ее относительной толщины и степени механической неоднородности
изменяется в достаточно широких пределах. Однако расчетная величина ![]() , вычисляемая по формуле (11),должна быть ограничена
значениями относительных толщин мягкой прослойки
, вычисляемая по формуле (11),должна быть ограничена
значениями относительных толщин мягкой прослойки ![]() .
.
Экспериментальная
проверка полученной методики.Экспериментальная проверка
расчетной методики по оценке величины ![]() сварных соединений, ослабленных
мягкими прослойками, была выполнена путем испытания на статический изгиб
сварных образцов. Первая группа образцов была выполнена из титановых сплавов. Основной
металл (Т) - из сплава ПТ-3В, с
временным сопротивлением
сварных соединений, ослабленных
мягкими прослойками, была выполнена путем испытания на статический изгиб
сварных образцов. Первая группа образцов была выполнена из титановых сплавов. Основной
металл (Т) - из сплава ПТ-3В, с
временным сопротивлением ![]() МПа. Сварка стыкового шва (М) былапроизведена по щелевой разделке кромок
неплавящимся электродом в среде аргона с использованием присадочной проволоки
из титанового сплава типа 2Вс
временным сопротивлением
МПа. Сварка стыкового шва (М) былапроизведена по щелевой разделке кромок
неплавящимся электродом в среде аргона с использованием присадочной проволоки
из титанового сплава типа 2Вс
временным сопротивлением ![]() МПа. Вторая группа испытываемых
образцов была выполнена по аналогичной технологии из мартенситностареющих
сталей. Основной металл (Т)
марки ЭП-678 (10Х11М2Т) с временным сопротивлением
МПа. Вторая группа испытываемых
образцов была выполнена по аналогичной технологии из мартенситностареющих
сталей. Основной металл (Т)
марки ЭП-678 (10Х11М2Т) с временным сопротивлением ![]() ; металл шва (М)-
из стали ЭП- 659 с временным сопротивлением
; металл шва (М)-
из стали ЭП- 659 с временным сопротивлением ![]() МПа.Степень механической неоднородности рассматриваемых
соединений составляла
МПа.Степень механической неоднородности рассматриваемых
соединений составляла![]() (для образцов из титановых сплавов) и
(для образцов из титановых сплавов) и ![]() (для образцов из мартенситностареющих сталей). Относительная
толщина мягкой прослойки – χ ,в качестве которой выступал сварной шов, варьировалась
путем изменения ширины щелевого зазора (h).Для реализацииусловий плоской деформации, по аналогии со статическим
растяжением, образцы для испытаний изготавливали с соотношением сторон
(для образцов из мартенситностареющих сталей). Относительная
толщина мягкой прослойки – χ ,в качестве которой выступал сварной шов, варьировалась
путем изменения ширины щелевого зазора (h).Для реализацииусловий плоской деформации, по аналогии со статическим
растяжением, образцы для испытаний изготавливали с соотношением сторон ![]() (рис.1) [4]. На рис. 3(а,б)приведено сопоставление расчетных и экспериментальных значений
(рис.1) [4]. На рис. 3(а,б)приведено сопоставление расчетных и экспериментальных значений ![]() для рассматриваемых соединений.
для рассматриваемых соединений.
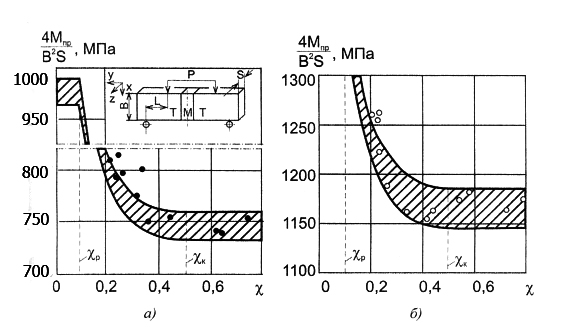
Рис.3.
Зависимость предельного изгибающего момента сварных соединений от
относительной толщины мягкой прослойки. Сравнение расчетных (по формуле 11) и
экспериментальных данных для сварных соединений титановых сплавов –( а): (![]() ) точки
- ( • ); и для мартенситностареющих сталей -(б): (
) точки
- ( • ); и для мартенситностареющих сталей -(б): (![]() )
точки - ( º )
)
точки - ( º )
При
испытании сварных образцов было замечено, что предельная стадия пластического
деформирования сопровождается большими
прогибами, оказывающими влияние на величину предельного изгибающего момента. В
связи с этим при расчетном определении величины ![]() влияние
данных прогибов производили путем введения в расчетную формулу (11)
соответствующей поправки ƒ. Величина данной поправки была получена из
следующих соображений (рис.4).
влияние
данных прогибов производили путем введения в расчетную формулу (11)
соответствующей поправки ƒ. Величина данной поправки была получена из
следующих соображений (рис.4).
![]() (12)
(12)
где
![]() - составляющая внешнего усилия, изгибающего образец;
- составляющая внешнего усилия, изгибающего образец; 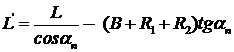 - плечо
усилий
- плечо
усилий ![]() при угле прогибасоединений
при угле прогибасоединений ![]() ; W–перемещение подвижных опор, соответствующее
предельному усилию;
; W–перемещение подвижных опор, соответствующее
предельному усилию; ![]() и
и ![]() - соответственно радиусы подвижных и неподвижных опор
(рис.4). Величина поправки ƒ на прогиб соединений при этом равна:
- соответственно радиусы подвижных и неподвижных опор
(рис.4). Величина поправки ƒ на прогиб соединений при этом равна:
![]() . (13)
. (13)
Величина
угла стрелы прогиба ![]() в процессе испытаний изменялась от 12° до 28°;
в процессе испытаний изменялась от 12° до 28°; ![]() мм, а
мм, а ![]() мм,
мм, ![]() мм - для
образцов из титановых сплавов;
мм - для
образцов из титановых сплавов; ![]() мм, а
мм, а ![]() мм,
мм, ![]() мм- для образцов из мартенситностареющих сталей.
мм- для образцов из мартенситностареющих сталей.
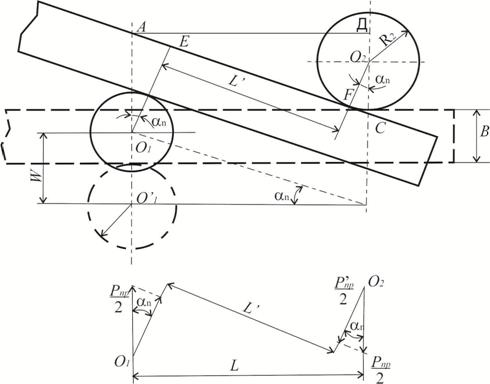
Рис.4. Расчетная схема для определения поправочной функции ƒ , учитывающей пластический прогиб соединения в процессе его нагружения
Выводы
1. Методом конечных элементов изучены особенности пластического деформирования механически неоднородных сварных соединений с мягкой прослойкой при изгибе, и на этой основе построены поля линий скольжения, позволяющие в аналитической форме проводить оценку напряженного состояния и предельной несущей способности рассматриваемых сварных соединений при данном виде нагружения.
2.На
величину предельного изгибающего момента сварных соединений ![]() в
значительной степени оказывают влияние степень механической неоднородности
в
значительной степени оказывают влияние степень механической неоднородности ![]() и
относительная толщина мягкой прослойки χ. С уменьшением χ предельный
изгибающий момент
и
относительная толщина мягкой прослойки χ. С уменьшением χ предельный
изгибающий момент ![]() увеличивается
по гиперболическому закону достигая максимума, соответствующего при
увеличивается
по гиперболическому закону достигая максимума, соответствующего при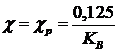 значениям
предельного изгибающего момента для пластины из твердого металла «Т».
значениям
предельного изгибающего момента для пластины из твердого металла «Т».
3.
Проверка расчетных зависимостей для определения ![]() на образцах из титановых сплавов и
мартенситностареющих сталей показала удовлетворительное соответствие
теоретических и опытных данных.
на образцах из титановых сплавов и
мартенситностареющих сталей показала удовлетворительное соответствие
теоретических и опытных данных.
Еремин Е.Н., д.т.н., профессор, заведующий кафедрой «Оборудование и технология сварочного производства»ОмГТУ, декан Машиностроительного института Омского государственного технического университета, г. Омск.
ШтенниковВ.С., д.т.н., профессор, директор Общества с ограниченной ответственностью «Удмуртский аттестационный центр «Национального Агентства Контроля и Сварки», г.Ижевск.
ПачуринГ.В., д.т.н., профессор, зав. кафедрой «Производственная безопасность и экология» (ПБиЭ), Нижегородский государственный технический университет им. Р.Е. Алексеева, г.Нижний Новгород.



