Электрические контакты представляют собой проводники, приведенные в соприкосновение путем приложения внешних механических сил и способные пропускать электрический ток. Области контактирования всегда являются источником дополнительного сопротивления. Имеются две основные причины его возникновения [2]. Первая из них – это возможное наличие на контактных поверхностях слабо проводящих пленок. Их влияние снижается при больших усилиях контактного нажатия (что характерно для сильноточных контактов), при высоких температурах, при нанесении гальванического покрытия на контакты или в том случае, когда контакты работают в условиях вакуума. В этой работе влияние пленок рассматриваться не будет.
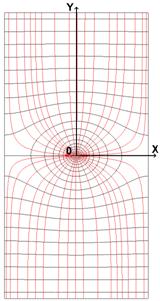
Второй причиной является эффект стягивания линий тока к контактным пятнам, через которые ток проходит из одного электрода в другой. Площадь контактных пятен может быть на несколько порядков меньше, чем кажущаяся поверхность контактирования. На рис. 1а приведено распределение линий тока и эквипотенциалей для случая двух цилиндрических электродов, соединенных одним проводящим пятном. Видно, что линии тока стягиваются к контактному пятну, а трубки тока, которые заключены между соседними линиями, при этом значительно сужаются. Это приводит к наличию сопротивления стягивания. В нашем случае, при отсутствии пленок, оно совпадает с контактным сопротивлением.
Распределение потенциала вдоль оси электродов качественно
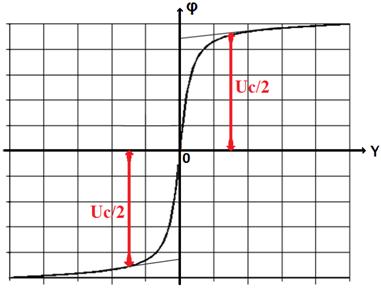
представлено на рис. 1б. Вдали от контактного пятна потенциал изменяется
линейно, при приближении к пятну наблюдается отклонение зависимости ![]() от линейной. Границу области стягивания
определим по величине указанного отклонения в 1%. Контактное сопротивление
равно отношению величины изменения потенциала в области стягивания к значению
протекающего тока
от линейной. Границу области стягивания
определим по величине указанного отклонения в 1%. Контактное сопротивление
равно отношению величины изменения потенциала в области стягивания к значению
протекающего тока ![]() . Для пятна круглой формы при
условии, что границы контактов достаточно удалены от области стягивания, ее
размер составляет порядка 5-6 радиусов контактного пятна.
. Для пятна круглой формы при
условии, что границы контактов достаточно удалены от области стягивания, ее
размер составляет порядка 5-6 радиусов контактного пятна.
а б
Рис. 1. Распределение линий тока и эквипотенциалей (а), распределение потенциала вдоль оси симметрии модели (б).
Поверхности любых электродов по своей форме не являются идеальными. Любые, даже специально обработанные, поверхности не являются абсолютно гладкими, что вызвано наличием отклонений разной природы и разного масштаба. Их принято разделять [1] на субшероховатость, шероховатость, волнистость (квазипериодические отклонения) и макроотклонения (единичные технологические дефекты поверхности).
Для слаботочных контактов, для которых характерные значения силы контактного нажатия, как правило, не превосходят единиц Ньютонов, значимыми оказываются отклонения всех уровней. Существующие математические модели позволяют оценить это влияние [2]. С увеличением силы контактного нажатия, а для сильноточных контактов ее величина измеряется десятками и сотнями Ньютонов, роль шероховатости и субшероховатости заметно снижается в силу возникающих значительных, в том числе пластических, деформаций в контактной области. В данной работе мы оценим степень влияния на характеристики электрических контактов неоднородностей более крупного масштаба – волнистости поверхности.
Исследуемая модель и результаты численных расчетов
Волнистость поверхности контактов может быть вызвана различными причинами, связанными в основном с технологией обработки при создании требуемой формы контактов, например с движением резца при фрезеровании. В качестве примера рассмотрим контактную поверхность сферической формы цилиндрического электрода, фотографии которого в разных проекциях приведены на рис. 2а и 2б. На рис. 2в и 2г приведены соответствующие профиллограмма (масштаб по вертикали: 5 мкм / 1 кл, по горизонтали: 250 мкм / 1 кл) и микрофотография. Такие электроды использовались нами при экспериментальном исследовании и численном моделировании прохождения ударных токов короткого замыкания через сильноточные контакты [3; 4]. Как на микрофотографии, так и на профиллограмме отчетливо видны чередующиеся кольцеобразные выступы и впадины. Это приводит к тому, что реальное контактное пятно, которое сформируется после приложения внешней силы, будет также содержать кольцеобразные непроводящие включения.
Проведем численные расчеты
прохождения тока через цилиндрические электроды, соединенные одним контактным
пятном круглой формы, которые помогут оценить вклад волнистости контактной
поверхности в сопротивление стягивания. Размеры электродов выбраны гораздо
большими размера контактного пятна, чтобы исключить влияние границ на параметры
контактов (данные о влиянии границ можно найти в [5]). На рис. 2д приведен увеличенный
фрагмент контактной области нижнего электрода. Внутри контактного пятна радиуса
а расположены чередующиеся
непроводящие и проводящие кольца, ширину которых обозначим b и с.
Величина k=b/c, задающая соотношение между ними, определяет степень фрагментации пятна.
При k=0 пятно не фрагментировано. Значение параметра k и количество непроводящих колец N будут варьируемыми параметрами. Такая приближенная
модель фрагментации пятна качественно соответствует приведенному выше профилю
рабочей поверхности. Будем следить за отклонением величины контактного
сопротивления при наличии фрагментации ![]() от аналогичной величины
от аналогичной величины ![]() в случае полностью проводящего пятна того же радиуса:
в случае полностью проводящего пятна того же радиуса:
![]() при изменении параметров k и N.
при изменении параметров k и N.


а б в

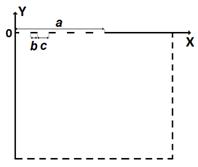
г д
Рис. 2. Фотографии электрода (а, б), профиллограмма (в) и микрофотография контактной поверхности (г), фрагмент контактной области расчетной модели (д).
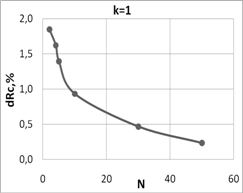
Рассмотрим сначала случай фрагментации пятна, когда проводящие и непроводящие кольца имеют равную ширину (k=1). При большом их числе площадь непроводящих включений составляет примерно половину от полной площади контактного пятна, т.е. степень фрагментации весьма значительна. Однако это практически не сказывается на величине контактного сопротивления (рис. 3а).
а б
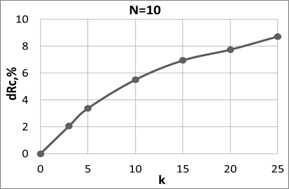
Рис. 3. Относительное увеличение контактного сопротивления, вызванное наличием фрагментации.
Зафиксируем теперь число непроводящих включений N=10 и будем изменять в широких пределах соотношение ширины проводящих и непроводящих колец 0≤k≤25. Это соответствует переходу от случая нефрагментированного пятна к пятну, у которого всего около 5% площади проводит ток. При этом, как следует из рис. 3б, контактное сопротивление возрастает менее чем на 10%.
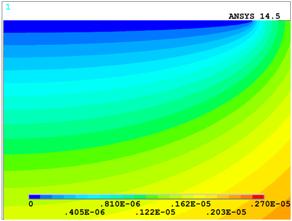
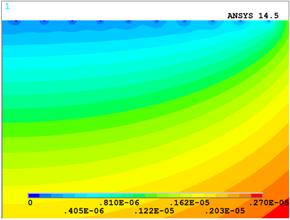
Для того чтобы объяснить столь слабое влияние фрагментации контактной поверхности на сопротивление стягивания, проанализируем распределения потенциала для случая N=10 и k=20. Сравним контурные распределения потенциала для этих случаев в окрестности контактного пятна (рис. 4).
а б
Рис. 4. Распределение потенциала в контактной окрестности для нефрагментированного случая (а) и с учетом фрагментации при N=10 и k=20 (б).
Качественные изменения наблюдаются только в области, непосредственно прилегающей к контактной поверхности. Назовем ее ближней зоной стягивания, в отличие от области стягивания к контактному пятну в целом, как мы это сделали во введении (дальняя зона стягивания). Здесь эквипотенциали искажаются в результате влияния фрагментации. Остальные же линии равного потенциала фрагментированием практически не искажены. Ближняя зона стягивания имеет размер, сравнимый с размером непроводящих включений.
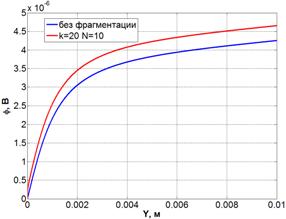
Более точно границу ближней зоны стягивания можно
определить из распределения потенциала вдоль оси симметрии модели (рис. 5а). Красная
линия соответствует нефрагментированной контактной поверхности, синяя – фрагментированной
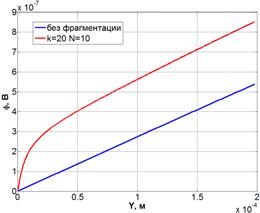
при N=10 и k=20. На рис.
5б приведен фрагмент этих распределений в малой окрестности контактного пятна.
На графике слева видно искажение распределения потенциала, вызванное наличием
дальнего стягивания. Ближнее стягивание также сказывается на распределении
потенциала. Его наличие приводит к тому, что красная линия смещена относительно
синей на величину «скачка» потенциала, вызванного наличием дополнительной
области стягивания. Размер этой области можно определить из рассмотрения
фрагмента, представленного на рис. 5б, по отклонению зависимости ![]() от линейной.
от линейной.
а б
Рис. 5. Распределение потенциала вдоль оси симметрии модели (а) и его фрагмент вблизи контактного пятна (б).
Заключение
Проведенные количественные оценки позволяют заключить, что для сильноточных контактов, если внешняя граница контактного пятна остается неизменной, фрагментация практически не влияет на величину контактного сопротивления, которое определяется в основном распределением электрического поля в дальней зоне стягивания. Таким образом, при проведении численных расчетов можно использовать приближение полностью проводящего контактного пятна, что делает расчетные модели менее требовательными к вычислительным ресурсам.
Рецензенты:Павлов В.А., д.ф.-м.н, профессор, физический факультет, кафедра радиофизики, Санкт-Петербургский государственный университет, г. Санкт-Петербург.
Бисярин М.А., д.ф.-м.н, профессор, физический факультет, кафедра радиофизики, Санкт-Петербургский государственный университет, г. Санкт-Петербург.



