Введение
Метод аналитического программирования [1-3] предназначен для задач, решениями которых являются нечисловые структуры. К таким задачам относится задача синтеза управления, решением которой является математическое выражение, описывающее функциональную зависимость управления от координат пространства состояния объекта. Метод аналитического программирования представляет собой разновидность метода генетического программирования [4-6]. Код метода аналитического программирования состоит из упорядоченного множества целых чисел, которые указывают на номера кодируемых структур. Простота кодирования определяет преимущества метода аналитического программирования.
Для эффективного применения метода аналитического программирования к решению задачи синтеза управления в работе представлен метод вариационного аналитического программирования. Данный метод позволяет сузить пространство поиска и задать область поиска за счет выбора базисного решения.
Постановка задачи синтеза системы управления
Задана модель объекта управления
![]() , (1)
, (1)
где ![]() ,
,
![]() ,
, ![]() –
ограниченное замкнутое множество.
–
ограниченное замкнутое множество.
Задана область начальных значений
![]() . (2)
. (2)
Заданы терминальные условия
![]() ,
, ![]() , (3)
, (3)
где ![]() – время окончания процесса управления,
оно может быть не задано, ограничено сверху,
– время окончания процесса управления,
оно может быть не задано, ограничено сверху, ![]() и
определяться выполнением терминальных условий (3).
и
определяться выполнением терминальных условий (3).
Задан функционал качества
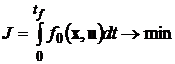 . (4)
. (4)
Необходимо найти управление в виде
![]() , (5)
, (5)
где ![]() ,
, ![]() ,
решение
,
решение ![]() системы
системы ![]() , обеспечивает удовлетворение ограничениям
на управление
, обеспечивает удовлетворение ограничениям
на управление ![]() , достижение терминальных
условий (3) и минимум функционала качества (4).
, достижение терминальных
условий (3) и минимум функционала качества (4).
Для решения задачи используем метод вариационного аналитического программирования.
1. Метод аналитического программирования
Введем упорядоченные множества функций с определёнными количествами аргументов
![]() ,
, ![]() ,
(5)
,
(5)
где ![]() – функция под номером
– функция под номером ![]() с количеством аргументов
с количеством аргументов ![]() ,
, ![]() ,
,
![]() .
.
Объединим все множества в одно
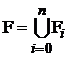 . (6)
. (6)
Пронумеруем все элементы объединённого множества
![]() , (7)
, (7)
где
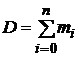 , (8)
, (8)
![]() ,
, ![]() ,…,
,…,
![]()
![]() ,…,
,…,
![]() ,
, ![]() ,…,
,…,
![]() .
.
Отдельно рассмотрим множество функций без аргументов или с нулевым количеством аргументов. Данное множество для математических выражений представляет собой множество параметров или переменных
![]() . (9)
. (9)
Запись кода математического выражения в методе аналитического программирования осуществляется в форме упорядоченного множества целых чисел
![]() , (10)
, (10)
где ![]() ,
, ![]() .
.
Каждое число указывает на номер элемента в объединенном
множестве ![]() (7). Запись
имеет префиксный порядок. Код функции в записи предшествует коду аргумента.
Длина записи кода ограничена. Дополнительное множество переменных и параметров
используется для корректного завершения записи. При необходимости код функции
из объединённого множества используется в виде кода для элемента множества
переменных или параметров.
(7). Запись
имеет префиксный порядок. Код функции в записи предшествует коду аргумента.
Длина записи кода ограничена. Дополнительное множество переменных и параметров
используется для корректного завершения записи. При необходимости код функции
из объединённого множества используется в виде кода для элемента множества
переменных или параметров.
Рассмотрим пример. Пусть задано множество функций
![]() ,
, ![]() ,
,
![]() .
.
Построим объединённое множество
![]() .
.
Объединённое множество содержит девять элементов ![]() . Множество переменных и параметров
содержит четыре элемента
. Множество переменных и параметров
содержит четыре элемента ![]() .
.
Пусть задана запись из восьми элементов
![]() .
.
Определяем вид математического выражения
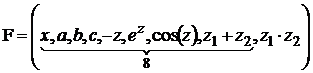 ,
, ![]() ,
,
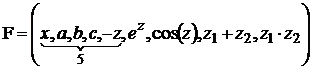 ,
, ![]() ,
,
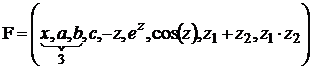 ,
, ![]() ,
,
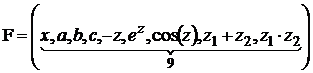 ,
, ![]() ,
,
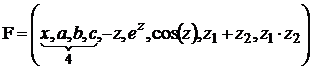 ,
, ![]() ,
,
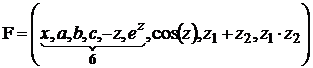 ,
, ![]() ,
,
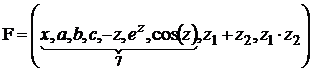 ,
, ![]() ,
,
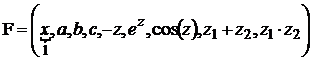 ,
, ![]() .
.
Для получения математического выражения из записи кода
необходимо знать количества элементов в каждом из множеств функций: ![]() ,…,
,…,![]() и
количества используемых переменных и параметров
и
количества используемых переменных и параметров ![]() и
и
![]() .
.
Количество аргументов функции ![]() и
номер функции
и
номер функции ![]() определяем по значению элемента
определяем по значению элемента
![]() кода математического выражения с помощью
соотношений
кода математического выражения с помощью
соотношений
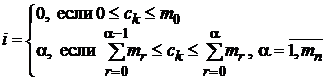 , (11)
, (11)
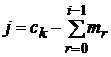 ,
, ![]() . (12)
. (12)
При соответствии элемента кода ![]() функции
без аргументов,
функции
без аргументов, ![]() для определения переменной
для определения переменной
![]() или параметра
или параметра ![]() необходимо
использовать количества используемых переменных
необходимо
использовать количества используемых переменных ![]() и
параметров
и
параметров ![]() .
.
![]() ,
, ![]() , (13)
, (13)
где код ![]() соответствует переменной
соответствует переменной ![]() , если
, если ![]() ,
или параметру
,
или параметру ![]() , если
, если ![]() .
.
Для описания кодов векторных математических выражений
используем один набор целых чисел с определенным количеством элементов для
каждого компонента векторного выражения. Пусть вектор математических выражений
имеет ![]() компонент. Выделим под каждую
компоненту вектора
компонент. Выделим под каждую
компоненту вектора ![]() позиций в коде записи.
Код математического выражения каждого компонента
позиций в коде записи.
Код математического выражения каждого компонента ![]() векторного
выражения содержит
векторного
выражения содержит ![]() элементов,
элементов, ![]() . Не используемым в формировании кода элементам
задаем нулевые значения
. Не используемым в формировании кода элементам
задаем нулевые значения
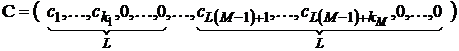 , (14)
, (14)
где ![]() – число позиций для кода одной компоненты
векторного выражения,
– число позиций для кода одной компоненты
векторного выражения, ![]() – длина кода
компоненты
– длина кода
компоненты ![]() векторного выражения,
векторного выражения, ![]() .
.
В коде записи векторного выражения (14) значения для элементов выполняются условия
![]() , если
, если ![]() ,
,
![]() . (15)
. (15)
Для расшифровки кода
векторного выражения необходимо вместе с величинами ![]() ,
,
![]() ,
, ![]() и
и
![]() дополнительно знать число позиций
дополнительно знать число позиций ![]() и длины кодов компонент
и длины кодов компонент ![]() ,
, ![]() .
.
Для определения
корректности записи кода математического выражения используем индекс элемента.
Пусть в записи кода (10) математического выражения элемент ![]() . Для векторного математического выражения
определим него номер компоненты
. Для векторного математического выражения
определим него номер компоненты ![]() из
соотношения
из
соотношения
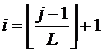 . (16)
. (16)
Для корректной записи для
индекса элемента ![]() необходимо выполнения
условий
необходимо выполнения
условий
![]() ,
, ![]() , (17)
, (17)
![]() . (18)
. (18)
где ![]() индекс элемента
индекс элемента ![]() записи кода математического выражения.
записи кода математического выражения.
Для вычисления индекса ![]() элемента
элемента ![]() при
условии
при
условии ![]() используем соотношение
используем соотношение
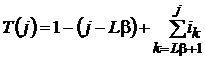 , (19)
, (19)
где
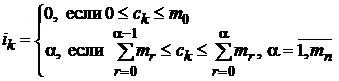 , (20)
, (20)
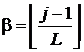 . (21)
. (21)
Индекс ![]() элемента
элемента ![]() указывает на минимальное число
недостающих справа элементов. Невыполнение условий (17) или (18) указывает на
неправильность записи математического выражения.
указывает на минимальное число
недостающих справа элементов. Невыполнение условий (17) или (18) указывает на
неправильность записи математического выражения.
Алгоритм для вычисления математического выражения по записи кода в аналитическом программировании должен располагать информацией о максимальном количестве аргументов в используемых функциях.
2. Метод вариации аналитического программирования
Пусть запись кода (10) определяет пространства записей
математических выражений. Пространство всех вариантов возможных записей длины ![]() для
для ![]() значений
кодов содержит
значений
кодов содержит ![]() элементов.
элементов.
Малой вариацией кода аналитического программирования является
изменение значения кода элемента ![]() . Одной малой
вариации достаточно для получения любой записи пространства из одной заданной
записи за конечное число вариаций.
. Одной малой
вариации достаточно для получения любой записи пространства из одной заданной
записи за конечное число вариаций.
Для описания малой вариации используем вектор из двух компонент
![]() , (22)
, (22)
где ![]() – номер позиции изменяемого кода элемента
записи,
– номер позиции изменяемого кода элемента
записи, ![]() – значение кода элемента.
– значение кода элемента.
Для выполнения вариации необходимо знать: количество
элементов в векторном выражении ![]() , количество
переменных
, количество
переменных ![]() , количество параметров
, количество параметров ![]() , количества используемых функций
определенной арности
, количества используемых функций
определенной арности ![]() ,
, ![]() ,…,
,…,![]() ,
количество выделенных для каждой компоненты позиций
,
количество выделенных для каждой компоненты позиций ![]() и
количество используемых в варьируемом коде позиций
и
количество используемых в варьируемом коде позиций ![]() ,
,
![]() .
.
Номер позиции ![]() в векторе вариации (22) не должен
превышать количество позиций в коде
в векторе вариации (22) не должен
превышать количество позиций в коде
![]() (23)
(23)
Значение кода элемента ![]() не
должно превышать количество элементов в объединенном множестве (22)
не
должно превышать количество элементов в объединенном множестве (22)
![]() , (24)
, (24)
где
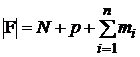 . (25)
. (25)
При выполнении вариации возможно получение некорректных записей. Проверку корректности записи кода осуществляем по условиям (17), (18). Для обеспечения корректности записи в зависимости от полученного в результате вариации кода записи изменяем значения некоторых последних кодов.
Для синтеза систем управления в большинстве случаев достаточно использовать объединённое множество переменных, параметров и функций следующего вида
![]()
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
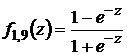 ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
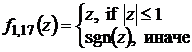 ,
, ![]() ,
,
![]() ,
, ![]() ,
,
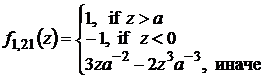 ,
, 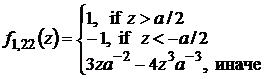 ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, 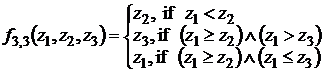 ,
,
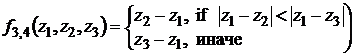 , (26)
, (26)
Пример синтеза системы управления
Рассмотрим применение метода вариационного аналитического программирования к решению задачи синтеза управления для системы третьего порядка с фазовыми ограничениями [3].
Задана система уравнений
![]() ,
,
![]() ,
,
![]() .
.
Заданы терминальные условия
![]() ,
, ![]() .
.
Заданы фазовые ограничения
![]() .
.
Задана область начальных значений
![]() ,
, ![]() ,
,
![]() .
.
Задан функционал
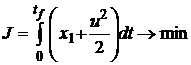 .
.
Необходимо найти управление в виде
![]() .
.
Для решения задачи используем метод вариационного аналитического программирования.
При решении использовали набор функций (26)
Базисное решение имело следующий вид
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() .
.
В результате применения метода было получено следующее решение
![]()
![]() ,
,
где ![]() ,
, ![]() .
.
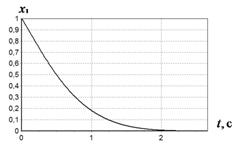
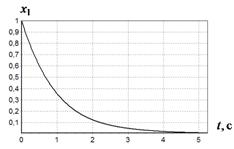
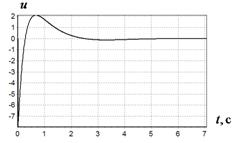
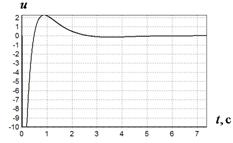
На рис. 1-4 приведены результаты моделирования системы с полученным решением.
а б
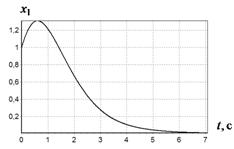
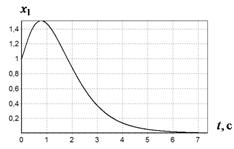
в г
Рис. 1 График изменения ![]() при различных начальных условиях:
при различных начальных условиях:
а - ![]() ,
, ![]() ;
б -
;
б - ![]() ,
, ![]() ;
;
в - ![]() ,
, ![]() ;
б -
;
б - ![]() ,
, ![]() ;
;
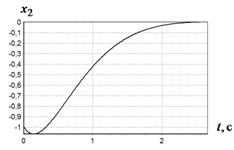
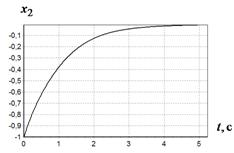
а б
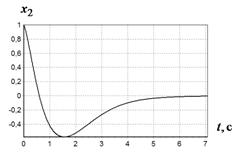
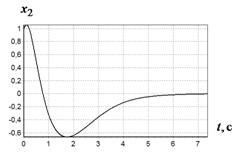
в г
Рис. 2 График изменения ![]() при различных начальных условиях:
при различных начальных условиях:
а - ![]() ,
, ![]() ;
б -
;
б - ![]() ,
, ![]() ;
;
в - ![]() ,
, ![]() ;
б -
;
б - ![]() ,
, ![]() ;
;
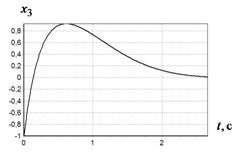
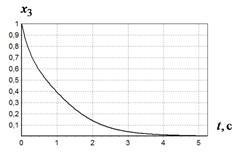
а б
в г
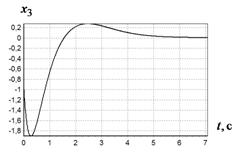
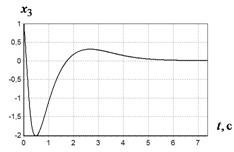
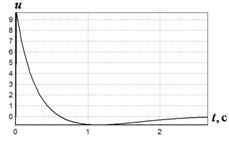
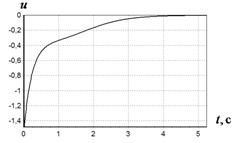
Рис. 3 График изменения ![]() при различных начальных условиях:
при различных начальных условиях:
а - ![]() ,
, ![]() ;
б -
;
б - ![]() ,
, ![]() ;
;
в - ![]() ,
, ![]() ;
б -
;
б - ![]() ,
, ![]() ;
;
а б
в г
Рис. 4 График изменения ![]() при различных начальных условиях:
при различных начальных условиях:
а - ![]() ,
, ![]() ;
б -
;
б - ![]() ,
, ![]() ;
;
в - ![]() ,
, ![]() ;
б -
;
б - ![]() ,
, ![]() ;
;
Из сказанного следует вывод, что метод вариационного аналитического программирования эффективен для решения задач синтеза управления.
Работа выполнена при финансовой поддержке гранта РФФИ № 14-08-00008-а «Исследование методов синтеза систем управления в условиях неопределенности».
Рецензенты:Забудский Е.И., д.т.н., профессор, ФГБОУ ВПО «Московский агроинженерный университет им. В.П. Горячкина», г. Москва.
Юрков Н.К., д.т.н., профессор, ФГБОУ ВПО «Пензенский государственный университет» Россия, г. Пенза.
Антонов А.В., д.т.н., профессор, декан факультета «Кибернетики», Обнинский институт атомной энергетики Национального исследовательского ядерного университета МИФИ Министерства образования и науки РФ, г. Обнинск.



