Введение
В курсе математики высшей школы неравенство Чебышева включено в систему теорем, которая получила название «Закон больших чисел» [1, 2, 4, 10]. Изложение этих теорем в рамках дисциплины «Математика» на инженерных специальностях и направлениях подготовки завершает рассмотрение основных вопросов теории вероятностей и подводит студентов к изучению раздела «Математическая статистика». В учебной литературе [1, 2, 4, 10] приводится формулировка отмеченного неравенства,его аналитическое доказательство и его применение при обосновании теорем Чебышева и Бернулли. Включение в теоретический материал небольшого количества задач[2, 4, 10], в которых предусмотрено использование неравенства Чебышева, несколько расширяет представление о содержанииэтого математического понятия.
Информация о существенных закономерностях вероятностных явлений, представленная в символизированных рассуждениях,достаточно трудно воспринимается студентами, планирующими получение инженерного образования, так как они, прежде всего,заинтересованы не в понимании того, как выводятся математические формулы, а как их можно использовать в решении практических задач и какие причинно-следственные взаимосвязи они отображают. Эффективным дидактическим средством, раскрывающим содержание понятий теории вероятностей, выступают графические модели, создающие их наглядное представление. Достижение понимания студентами различных функциональных зависимостей происходит при восприятии их графиков, построение которых требует проведение имитационного моделирования или вычислительного эксперимента.
Современное программное обеспечение персональных компьютеров позволяет не только быстро создавать большие массивы числовых данных, но и строить их графические модели, поэтому введение информационных технологий в учебный процесс расширяет банк методических идей по совершенствованию путей формирования математических понятий. Возможный вариант включения имитационного моделирования в дидактическое сопровождение для иллюстрации теоремы Бернулли предложен в публикации [5], а применение вычислительного эксперимента для построения графической модели, раскрывающей существенные взаимосвязи неравенстваЧебышева, представлено в данной работе.
Результаты и обсуждение
Отбор учебно-теоретического материала. Занимаясь изучением случайных явлений, великий русский математик П.Л. Чебышев (1821–1894) установил соотношение между дисперсией случайной величины и вероятностью превышения некоторого заданного числа отклонения её значений относительно математического ожидания. Результаты проведенного исследования нашли свое отражение в работе «О средних величинах», опубликованной в 1867 году [8, с. 221]. Запись неравенства Чебышева имеет следующий вид
где X – случайная величина, MX – математическое ожидание случайной величины X,DX – дисперсия случайной величины X, a – положительное число[3, с.115].
Неравенство (1) утверждает, что, каково
бы ни было положительное число а,
вероятность того, что случайная величина Х
отклонится от своего математического ожидания не меньше чем на a, ограничена сверху величиной, равной
отношению её дисперсии к квадрату числа a. Если число a выразить в единицах σ![]() ,
то неравенство (1) можно записать в виде
,
то неравенство (1) можно записать в виде
![]()
где σ–стандартное отклонение случайной величины Х, k – кратность σ.
В работе [1] неравенство Чебышева представлено в виде неравенства (1). При записи неравенства (1) в работах [4,10] вместо символа a используется символ ?. Введение ? затрудняет понимание смысла неравенства (1), так как ? воспринимается студентами как бесконечно малая величина, а в случае неравенства (1) положительное число a не обязательно должно быть бесконечно малой величиной. В работе [2]неравенство Чебышева представлено в виде
![]()
Понимание содержания неравенства (3) затрудняет интерпретация ситуации, когда правая часть становится отрицательной, что значительно осложняет процесс формирования этого понятия в учебном процессе. Обобщение результатов анализа определения понятия «неравенство Чебышева» в работах [1, 2, 4, 10] делает целесообразным использование методики его формирования, предложенной Е.С. Вентцель[1]. Изложение учебного материала в этом подходе сопровождается построением графической модели (рис. 1), иллюстрирующей расположение на осиОхзначений случайной величиныХ, ее математического ожиданияMХи некоторого заданного числа а(точки А и Bудалены от MXна расстояние а) [1, с.288].

Рис. 1. Расположение значений случайной величины Х
Представленный наглядный образ (рис. 1) визуализирует
взаимосвязипонятия![]() (вероятностьпопадания случайной точки вне отрезка АВ), но не его соотношение с дисперсией DX. Утверждение, зафиксированное в
неравенстве (1) аналитически доказывается как для дискретной случайной величины,
так и для непрерывной случайной величины[1].
(вероятностьпопадания случайной точки вне отрезка АВ), но не его соотношение с дисперсией DX. Утверждение, зафиксированное в
неравенстве (1) аналитически доказывается как для дискретной случайной величины,
так и для непрерывной случайной величины[1].
Идея экспериментального
исследования.
Отношение понятийDX
и![]() выводится
аналитически и процесс рассуждения не всегда убеждает студентов не математических
специальностей и направлений подготовки в его истинности, проявляющейся в объективной
реальности. Построение наглядного образа этого соотношения с помощью графиков
функций
выводится
аналитически и процесс рассуждения не всегда убеждает студентов не математических
специальностей и направлений подготовки в его истинности, проявляющейся в объективной
реальности. Построение наглядного образа этого соотношения с помощью графиков
функций ![]() и
и
![]() создает
условия для обсуждения со студентами проблемы взаимосвязи теоретического и
эмпирического способов познания окружающей действительности.
создает
условия для обсуждения со студентами проблемы взаимосвязи теоретического и
эмпирического способов познания окружающей действительности.
Постановка
вычислительного эксперимента. Формой экспериментальной проверки
неравенства (1) для дискретных и непрерывных случайных величин может выступать
выполнение лабораторно-практическогозадания
«Экспериментальное определение вероятности попадания случайной величины вне
заданного интервала». Цель учебно-исследовательской деятельности: составление
умозаключений на основе сопоставления результатов аналитических доказательств
и графического моделирования. Ход работы состоит из шести этапов: 1) формирование массива значений случайной
величины Х; 2) вычисление математического
ожиданияMX,
дисперсииDX
и стандартного отклонения σ; 3) определение значений центрированной
случайной величины ![]() (отклонение
случайной величины
(отклонение
случайной величины ![]() от
математического ожидания MX;
4) нахождение вероятности
от
математического ожидания MX;
4) нахождение вероятности![]() при
различныхзначениях
при
различныхзначениях![]() ;
5) построение графиков функций
;
5) построение графиков функций ![]() и
и
![]() ;
6) сравнение расположенияграфиков функций
;
6) сравнение расположенияграфиков функций ![]() и
и
![]() на
координатной плоскости друг относительно друга. Рассмотрим содержание учебной
деятельности предлагаемого лабораторно-практического задания.
на
координатной плоскости друг относительно друга. Рассмотрим содержание учебной
деятельности предлагаемого лабораторно-практического задания.
Первый этап. Пакет программ «Анализ данных» электронных таблиц Excel имеет в своей библиотеке программу «Генерация случайных чисел» (ГСЧ) [9]. Эта программа в автоматическом режиме может создавать массивы числовых данных дискретных и непрерывных случайных величин. Согласно предельной теореме теории вероятностей распределение случайной величины будет приближаться к нормальному распределению, когда результаты наблюдений формируются под действием большого числа независимо действующих факторов [1, 2, 4], поэтому представляется целесообразным использовать его для иллюстрации неравенства (1). Объем выборочных данных nопределяется доверительной вероятностью (надежностью) γ, стандартным отклонением σ*и точностью оценки математического ожидания δ. Значение nвычисляется по формуле
![]()
где
t
находится из уравнения ![]() ,
,
![]() –
функция Лапласа [2].
–
функция Лапласа [2].
В учебных задачах, как правило, γ
задается значениями 0.95, 0.99 и 0.999. Например, для исследования с
доверительной вероятностью ![]() нормально
распределенной случайной величины Х
с параметрами
нормально
распределенной случайной величины Х
с параметрами ![]() и
и
![]() ,
необходимо ввести в программу ГСЧ начальные условия:
,
необходимо ввести в программу ГСЧ начальные условия: ![]() ,
,
![]() ,
,
![]() .
Программа в автоматическом режиме сформирует массив данных (таблица 1).
.
Программа в автоматическом режиме сформирует массив данных (таблица 1).
Таблица 1
Случайная величина Х
|
7,40 |
6,62 |
7,35 |
11,32 |
5,11 |
2,84 |
9,39 |
8,14 |
12,41 |
8,89 |
|
5,44 |
4,62 |
7,26 |
4,78 |
6,31 |
10,90 |
8,65 |
9,66 |
10,89 |
9,24 |
|
8,49 |
4,31 |
10,69 |
9,08 |
4,96 |
5,44 |
6,12 |
9,72 |
10,61 |
8,43 |
|
10,55 |
6,04 |
7,83 |
9,80 |
7,27 |
6,69 |
7,52 |
6,73 |
8,23 |
5,95 |
|
10,40 |
6,45 |
7,63 |
11,84 |
7,94 |
9,52 |
8,26 |
6,15 |
8,00 |
10,48 |
|
11,47 |
3,76 |
6,97 |
7,83 |
8,06 |
8,93 |
9,12 |
10,22 |
8,91 |
7,38 |
|
3,63 |
6,86 |
11,94 |
6,95 |
7,35 |
9,75 |
8,28 |
5,60 |
7,95 |
6,32 |
|
7,53 |
7,19 |
9,73 |
9,35 |
12,39 |
9,19 |
6,18 |
4,88 |
5,89 |
6,36 |
|
10,19 |
8,27 |
12,75 |
7,24 |
4,52 |
5,26 |
11,77 |
9,42 |
4,45 |
7,14 |
|
5,83 |
7,27 |
6,69 |
9,52 |
6,53 |
5,77 |
8,97 |
9,28 |
9,66 |
7,09 |
Объем данных ![]() удовлетворяет
точности оценки математического ожидания
удовлетворяет
точности оценки математического ожидания ![]() при
при
![]() .
Формула (4) позволяет проверить значение
.
Формула (4) позволяет проверить значение ![]() (δ
= 1.96/10 =0.196≈ 0.2, 2Ф(1.96) = 0.95,
(δ
= 1.96/10 =0.196≈ 0.2, 2Ф(1.96) = 0.95, ![]() ).
).
Второй этап. Расчет математического ожидания MXи дисперсии DX осуществляется в автоматическом режиме с помощью функций СРЗНАЧ и ДИСПР электронных таблиц Excel[9]. Функции СРЗНАЧ и ДИСПР производят вычисления MXи DX по формулам

где n – количество значений случайной величины.
Математическое ожидание, дисперсия и стандартное
отклонение случайной величины Х(таблица
1) принимают значения ![]() ,
,
![]() и
и
![]() .
.
Третий этап. Для вычислениязначений центрированной
случайной величины ![]() может
использоваться математическая функцияABS электронных таблиц Excel [9]. Значения
может
использоваться математическая функцияABS электронных таблиц Excel [9]. Значения![]() ранжируются
по возрастанию(таблица 2).
ранжируются
по возрастанию(таблица 2).
Таблица 2.
Центрированная
случайная величина ![]()
|
0,04 |
0,37 |
0,63 |
0,99 |
1,28 |
1,58 |
1,83 |
2,32 |
2,94 |
3,59 |
|
0,05 |
0,37 |
0,63 |
1,01 |
1,29 |
1,59 |
1,85 |
2,46 |
2,99 |
3,87 |
|
0,07 |
0,38 |
0,64 |
1,03 |
1,34 |
1,62 |
1,86 |
2,46 |
3,00 |
3,94 |
|
0,07 |
0,38 |
0,66 |
1,04 |
1,37 |
1,62 |
1,90 |
2,50 |
3,02 |
4,04 |
|
0,10 |
0,50 |
0,71 |
1,07 |
1,38 |
1,72 |
1,95 |
2,58 |
3,12 |
4,14 |
|
0,16 |
0,52 |
0,75 |
1,17 |
1,45 |
1,75 |
2,01 |
2,64 |
3,28 |
4,27 |
|
0,24 |
0,53 |
0,76 |
1,18 |
1,45 |
1,76 |
2,07 |
2,65 |
3,38 |
4,49 |
|
0,27 |
0,55 |
0,81 |
1,21 |
1,49 |
1,76 |
2,13 |
2,71 |
3,42 |
4,51 |
|
0,33 |
0,55 |
0,93 |
1,21 |
1,52 |
1,78 |
2,29 |
2,79 |
3,45 |
4,85 |
|
0,36 |
0,59 |
0,95 |
1,22 |
1,54 |
1,82 |
2,30 |
2,79 |
3,57 |
5,06 |
Четвертый этап. Экспериментально полученные значения ![]() позволяют
найти искомую вероятность
позволяют
найти искомую вероятность ![]() по
формуле
по
формуле
![]()
где
![]() m(k) – количество
m(k) – количество ![]() ,n – количество значений случайной
величины Х (в демонстрационном
примере n
= 100). Величина
,n – количество значений случайной
величины Х (в демонстрационном
примере n
= 100). Величина![]() устанавливается
непосредственным подсчетом количества чисел (таблица 2), значения которых
удовлетворяют неравенству
устанавливается
непосредственным подсчетом количества чисел (таблица 2), значения которых
удовлетворяют неравенству ![]() .
.
Пятый этап. Построение графиков функций![]() и
и
![]() осуществляется
с помощью подпрограммы Точечный график программы Мастер диаграмм электронных
таблиц Excel[9] (рис. 2).
осуществляется
с помощью подпрограммы Точечный график программы Мастер диаграмм электронных
таблиц Excel[9] (рис. 2).
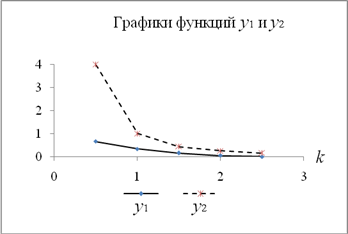
Рис. 2.Графики
функций ![]() и
и
![]()
Ломаная линия, соответствующая графику
функции ![]() ,
соединяет точки с координатами
,
соединяет точки с координатами![]() (рис.
2). Ломаная линия, соответствующая графику функции
(рис.
2). Ломаная линия, соответствующая графику функции ![]() ,соединяет
точки с координатами
,соединяет
точки с координатами ![]() (рис.
2).
(рис.
2).
Шестой этап. График функции ![]() располагается
ниже графика функции
располагается
ниже графика функции![]() (рис.
2), следовательно, выполняются неравенства
(рис.
2), следовательно, выполняются неравенства ![]() и
(1).Результаты вычислительного эксперимента согласуются с утверждением
неравенства Чебышева. При увеличении kграфики функций
и
(1).Результаты вычислительного эксперимента согласуются с утверждением
неравенства Чебышева. При увеличении kграфики функций ![]() и
и
![]() асимптотически
приближаются к осиОх, а расстояние
между ними уменьшается, но неравенство
асимптотически
приближаются к осиОх, а расстояние
между ними уменьшается, но неравенство ![]() сохраняется.
сохраняется.
Программа ГСЧ электронных таблиц Excel[9]может формировать значения случайных величин, имеющих нормальное, равномерное, биномиальное распределения или распределения Бернулли, Пуассона, что позволяет составлять различные лабораторно-практические задания для экспериментального определения вероятности попадания случайной величины вне заданного интервала.
Формирование понятия. Изучение неравенства Чебышева студентами технических специальностей и направлений подготовки может осуществляться в следующей последовательности: 1) символьное и вербальное определение неравенства; 2) аналитическое доказательство для дискретных и непрерывных случайных величин; 3) выполнение представленного лабораторно-практического задания; 4) решение учебных задач (определение по заданной дисперсии вероятности попадания случайной величины в некоторой симметричный относительно математического ожидания интервал или оценивание длины интервала по известной дисперсии[2, 4, 10]).
Заключение
Предложенное дополнение к методическому обеспечению по формированию одного из понятий теории вероятностей ставит своей целью включение студентов в исследовательскую деятельность, требующую освоения теоретических и экспериментальных методов познания. Прохождение выделенных четырех этапов формирования понятия «неравенство Чебышева» требует построения разнообразных аналитико-синтетических рассуждений, что создает условия для развития культуры мышления и творческих способностей студентов при изучении вероятностных закономерностей в учебном процессе [6, 7].
Рецензенты:СтружановВ.В., д.ф.-м.н., профессор, главный научный сотрудник Института машиноведения УрО РАН, г.Екатеринбург.
ГотлибБ.М., д.т.н., профессор, заведующий кафедрой «Мехатроника» Уральского государственного университета путей сообщения, г.Екатеринбург.




