Введение
Современный уровень развития передачи и приема информации ставит задачу высокой помехоустойчивой системы. Дуплексные системы передачи в настоящее время широко распространены в системах телекоммуникаций. Используются в двух вариантах: двух- и четырехпроводном. Разумеется, дуплексная передача по двухпроводному каналу является экономически более выгодной, однако технически более сложно реализуема. Причиной является необходимость компенсации эхо-сигналов. Причина возникновения эхо-сигналов – разбалансировка дифференциальной системы, разделяющей направления передач. Известны различные методы компенсации эхо-сигналов: с помощью модели эхо-тракта в виде трансверсального фильтра или путем выборки необходимых образцов эхо-сигналов из блока памяти при табличном методе компенсации. В первом случае для работы эхокомпенсатора требуется производить большое количество операций умножения и сложения, а во втором необходим большой объем памяти для хранения всех возможных образцов эхо-сигналов. В последние годы появился новый метод эхокомпенсации, который в литературе называется по-разному: относительный, инвариантный. Исследованию этого метода посвящено немало публикаций, а также диссертационных исследований, включая докторские диссертации. Однако всем этим исследованиям присущ существенный недостаток – все внимание уделено анализу частотных искажений, вносимых в принимаемый сигнал эхокомпенсатором, при полном игнорировании влияния сигналов собственного передатчика на работу эхокомпенсатора. Отсутствует также исследование влияния разбалансировки дифференциальной системы, которая может произойти после окончания обучения эхокомпенсатора. Отсутствие этих исследований не позволяет дать рекомендации по практическому применению инвариантных эхокомпенсаторов. Одним из возможных подходов к решению данной задачи является совместное использование метода относительной амплитудной модуляции и инвариантного подхода передачи сообщений [1, 3].
Новый метод адаптации инвариантного эхокомпенсатора
На основе недавно предложенного метода адаптации инвариантного эхокомпенсатора [2], основанного на том, что погрешность эхокомпенсации повторяет форму сигнала с точностью до коэффициента ослабления отсчетов передаваемых сигналов, проходящих через дифференциальную систему, то есть с точностью до k, был разработан новый метод адаптации инвариантного эхокомпенсатора.
При разбалансировки дифференциальной системы, сигнал на выходе эхокомпенсатора равен
![]() , (1)
, (1)
где, ![]() –
погрешность эхокомпенсации.
–
погрешность эхокомпенсации.
Если умножить сумму погрешности эхокомпенсации
и сигнала противоположной стороны на передаваемый сигнал [4], то получится
следующее выражение: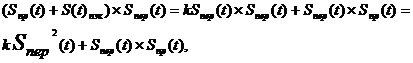 (2)
(2)
Затем проинтегрируем на промежутке Т и разделить на Т получим:
![]() (3)
(3)
Так как интегрирование синусоиды равно нулю, то из этого следует, что произведение сигналов на входе и на выходе тоже будет стремиться к нулю:
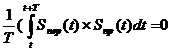 (4)
(4)
Тогда формула приобретает следующий вид:
![]() (5)
(5)
Отсюда следует, что если взять интеграл квадрата передаваемого сигнала на том же промежутке, что будет являться энергией сигнала, на который поделим выражение 5, то сможем найти k, [5]:
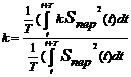 (6)
(6)
Исходя из этого, можно сделать вывод о том, что адаптация инвариантного эхокомпенсатора возможна. Адаптивная структурная схема инвариантного эхокомпенсатора представлена на (рис. 1).
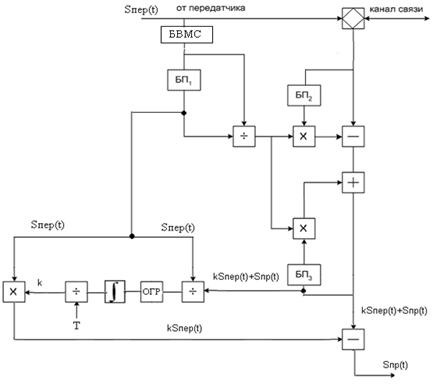
Рисунок 1. Схема адаптивного инвариантного эхокомпенсатора
Результаты экспериментального исследования адаптивного инвариантного эхокомпенсатора и анализ полученных данных
Для получения результатов была получена моделирующая программа, написания в среде Matlab, для имитации процессов, происходящих при обучении и дальнейшей работе предложенной схемы адаптивного инвариантного эхокомпенсатора.
Качество работы предложенной схемы оценивается величиной среднего квадратичного отклонения (СКО) при разных уровнях шума.
Были рассмотрены три варианта организации работы схемы эхокомпенсатора при введении помехи в виде белого шума. В первом случае эхо-компенсатор без преобразований, то есть только при наличии дифференциальной системы с изменяющимися параметрами; во втором – эхокомпенсатор плюс схема адаптации и схема вычитания передаваемого сигнала; в третьем – эхокомпенсатор и схема адаптации. Для наглядного сравнения также показаны изменения помехи в виде белого шума.
В качестве исследуемого сигнала был взят синусоидальный сигнал как основной, однако для сравнения был исследован при таких же условиях сигнал прямоугольной формы.
Результаты исследования влияния помехи в виде белого шума на качество эхокомпенсации при различных вариантах организации работы схемы представлены в последующих таблицах (1,2,3), аграфики исследования показаны на рисунках (2,3,4).
Рассмотрим зависимость СКО от количества проведенных испытаний.
Для синусоидального сигнала: при коэффициенте рассогласования дифференциальной системы, равным 0,5, и дисперсии белого шума, равной 0,1.
Таблица 1. Зависимость СКО от количества испытаний при синусоидальной форме сигнала
|
n |
30 |
50 |
100 |
500 |
1000 |
5000 |
10000 |
50000 |
|
vv |
0,5988 |
2,0124 |
0,8778 |
2,1196 |
2,276 |
2,1224 |
2,1318 |
2,1463 |
|
vv1 |
2,2587 |
0,6828 |
0,7797 |
3,7203 |
4,4549 |
4,2234 |
4,3432 |
4,2189 |
|
vv2 |
0,3356 |
0,3264 |
0,3109 |
0,3601 |
0,3617 |
0,3547 |
0,3562 |
0,3563 |
|
vv3 |
3,251 |
3,325 |
2,4185 |
0,5894 |
0,3625 |
0,356 |
0,3803 |
0,3577 |
|
y |
20,6126 |
21,8382 |
22,7966 |
21,9027 |
21,561 |
21,6537 |
21,6685 |
21,7108 |
Используемые обозначения:
vv – эхокомпенсатор без преобразований;
vv1 – эхокомпенсатор, схема адаптации и вычитание передаваемого сигнала;
vv2 – помеха в виде белого шума;
vv3 – эхокомпенсатор, схема адаптации;
y – уровень вводимого шума, дБ;
n – количество испытаний.
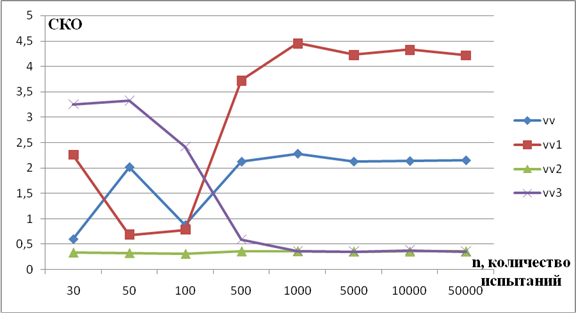
Рисунок 1. График зависимости СКО от количества испытаний при синусоидальном сигнале
На данном графике представлена зависимость СКО от количества испытаний при различных вариантах работы схемы эхокомпенсатора. Как видно из рисунка 1, характер кривых отличается. Рассмотрим первоначально промежуток от 30 до 500 испытаний. На данном этапе наибольшие значения СКО принимает в предложенной схеме с адаптацией; наименьшие – при той же схеме, но с добавлением элемента вычитания. При увеличении числа испытаний на порядок ситуация меняется в противоположную сторону. Средняя квадратичная ошибка для схемы с адаптацией практически сравнивается по своей величине со значениями помехи в виде белого шума. Значит, предложенная схема не вносит дополнительные помехи в передаваемый сигнал, что говорит о ее адаптивности, а соответственно, и о ее работоспособности. По полученным данным также видно, что с увеличением количества испытаний графики выравниваются, что указывает на их постоянный характер.
Для того чтобы точнее оценить и сравнить прохождение сигнала передачи, приведем пример подобного исследования для сигнала передачи прямоугольной формы.
Как видно из полученных результатов исследования, кривые фактически не поменяли характер своего развития и направления, несмотря на изменение формы сигнала (синусоидальный, прямоугольный).
Таблица 2
Зависимость СКО от количества испытаний при прямоугольной форме сигнала
|
n |
30 |
50 |
100 |
500 |
1000 |
5000 |
10000 |
50000 |
|
vv |
2,5617 |
2,8115 |
2,6498 |
2,7006 |
2,9576 |
2,9117 |
2,9007 |
2,9392 |
|
vv1 |
3,4442 |
2,4543 |
2,1791 |
3,8142 |
5,5267 |
5,7596 |
5,8241 |
5,7853 |
|
vv2 |
0,3322 |
0,3029 |
0,339 |
0,3409 |
0,3611 |
0,3594 |
0,3555 |
0,3557 |
|
vv3 |
1,6741 |
3,1191 |
3,1245 |
1,6253 |
0,5133 |
0,3621 |
0,3582 |
0,3607 |
|
y |
15,4004 |
22,7079 |
25,9759 |
24,7679 |
24,9426 |
24,3329 |
24,5055 |
24,4788 |
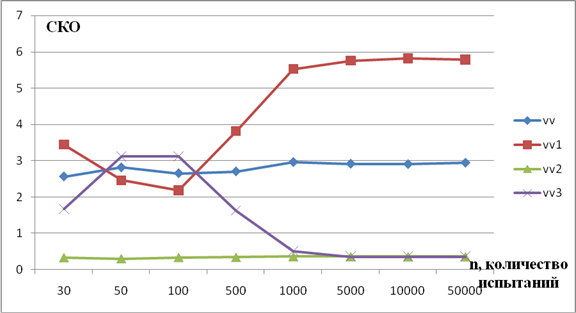
Рисунок. График зависимости СКО от количества испытаний при прямоугольной форме сигнала
Также по результатам эксперимента построены графики зависимости среднего квадратичного отклонения (СКО) от коэффициента рассогласования дифференциальной системы, равным 0,5, и дисперсии белого шума, равной 0,1 при синусоидальном сигнале, которые представлены в таблице 3, на рис. 3;
где, VV – эхокомпенсатор без преобразований, то есть только при наличии дифференциальной системы с изменяющимися параметрами;
VV1 – эхокомпенсатор плюс схема адаптации и схема вычитания передаваемого сигнала;
VV2 – помеха в виде белого шума;
VV3 – эхокомпенсатор и схема адаптации;
У – уровень вводимого шума, дБ;
k – коэффициент рассогласования.
Как видно из полученных результатов, показанных в таблице 3 и графиках, изображенных на рисунке 3, которые соответствуют помехе в виде белого шума и схеме с адаптацией, имеют очень близкие значения, отличающиеся в сотых долях. Такая тенденция говорит опять же о том, что предложенная структурная схема не вносит дополнительных помех при прохождении передаваемого сигнала.
Таблица 3
Зависимость СКО от коэффициента рассогласования дифференциальной системы
|
k |
0,1 |
0,5 |
1 |
2 |
5 |
10 |
|
vv |
0,5434 |
2,1125 |
4,1631 |
8,3123 |
22,2923 |
43,6164 |
|
vv1 |
4,2142 |
0,3034 |
4,319 |
4,0982 |
4,5251 |
4,4692 |
|
vv2 |
0,3564 |
0,3541 |
0,3533 |
0,3587 |
0,3548 |
0,3586 |
|
vv3 |
0,361 |
0,3709 |
0,3849 |
0,3656 |
0,3587 |
0,3705 |
|
y |
21,783 |
21,7398 |
21,9222 |
21,5536 |
21,7073 |
21,6202 |
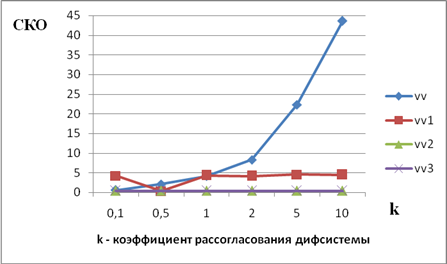
Рисунок 3. График зависимости СКО от коэффициента рассогласования дифференциальной системы при синусоидальном сигнале
Заключение
Полученные результаты, показывающие зависимость средней квадратичной ошибки (СКО) от дисперсии белого шума при различных формах сигналов, подтверждают предыдущие показания, то есть доказывают, что предложенная схема адаптивного инвариантного эхокомпенсатора является работоспособной в условиях действия помехи в виде белого шума.
Рецензенты:Сединин В.И., д.т.н., профессор, зав. кафедрой «Систем автоматизированного проектирования», ФГОБУ ВПО «СибГУТИ», г. Новосибирск.
Носов В.И., д.т.н., профессор, заведующий кафедрой «Систем радиосвязи» ФГОБУ ВПО «СибГУТИ», г. Новосибирск.



