Введение
Решение проблемы обеспечения надёжности распределенных систем сбора и обработки информации (РССОИ) в условиях ресурсных ограничений предполагает обязательность проработки вопросов организации технической эксплуатации РССОИ, начиная с самых ранних этапов их жизненного цикла. Подобные задачи возникают при изменении технического состояния, израсходовании технического ресурса, а также при модернизации и замене компонентов уже функционирующих РССОИ [5]. Решение этих задач требует разработки методов синтеза (определения значений параметров) системы технической эксплуатации (СТЭ) РССОИ. Для описания и сравнения различных вариантов организации эксплуатации при синтезе СТЭ необходимо разработать математическую модель функционирования СТЭ РССОИ.
Цель исследования
Разработка математической модели функционирования системы технической эксплуатации распределенной системы сбора и обработки информации.
Исходные предположения и допущения метода исследования
Будем считать, что структура распределенной системы сбора и обработки информации задана множеством D = {di}, ![]() Работоспособность РССОИ может в общем случае обеспечиваться несколькими (J) подмножествами элементов Dj Ì D, (
Работоспособность РССОИ может в общем случае обеспечиваться несколькими (J) подмножествами элементов Dj Ì D, (![]() ).
).
Успешность выполнения возложенных на РССОИ функций будет определяться событием, состоящим в том, что в определённый момент времени в работоспособном состоянии будет находиться любое подмножество Dj Ì D (![]() ), состав элементов которого достаточен для обеспечения заданного множества функций.
), состав элементов которого достаточен для обеспечения заданного множества функций.
Функция работоспособности системы, состоящей из множества элементов D, определяется логической функцией (в форме конъюнкции).
![]() ,
,
где х* – множество состояний системы, Dj – множество элементов, обеспечивающих выполнение системой целевых функций
![]()
Поскольку несколько наборов работоспособных элементов могут обеспечивать работоспособность всей системы, функция работоспособности системы, состоящей из множества элементов Dj, может быть выражена через функции работоспособности ![]() ; в дизъюнктивной нормальной форме (ДНФ) [4]:
; в дизъюнктивной нормальной форме (ДНФ) [4]:
![]() .
.
При этом функция работоспособности ![]() = 1, если в множестве элементов D имеется хотя бы одно подмножество элементов, работоспособность которых обеспечивает работоспособность системы.
= 1, если в множестве элементов D имеется хотя бы одно подмножество элементов, работоспособность которых обеспечивает работоспособность системы.
Система технической эксплуатации на практике, как правило, имеет двух – трёхуровневую структуру. Рассмотрим случай, когда используется двухуровневая структура системы технической эксплуатации (СТЭ).
Пусть система содержит ![]() элементов, в составе которых используется R типов средств, различающихся с точки зрения элементной базы, параметров надёжности и целевых функций. Число средств типа r,
элементов, в составе которых используется R типов средств, различающихся с точки зрения элементной базы, параметров надёжности и целевых функций. Число средств типа r, ![]() на n-м элементе обозначим
на n-м элементе обозначим ![]() , а общее число средств равно Н.
, а общее число средств равно Н.
В случае отказа локализация неисправности производится эксплуатирующим персоналом, им же производится восстановление работоспособности агрегатным методом, если в комплекте запасных инструментов и принадлежностей (ЗИП) имеется необходимый элемент замены (т.е. имеет место резервирование данного элемента).
Неисправный узел (блок) восстанавливается в специализированном ремонтном органе с использованием обезличенного метода ремонта. Этот же ремонтный орган производит восстановление работоспособности средства в случае, если в ЗИПе не оказалось необходимого элемента замены, либо эксплуатирующему персоналу не удалось самостоятельно локализовать и устранить неисправность.
Разработка модели
Для формализованного представления описанных обслуживаемых средств и подсистемы поддержания и восстановления работоспособности СТЭ РССОИ целесообразно использовать математический аппарат локально сбалансированных сетей массового обслуживания [2].
Обслуживаемая распределенная система сбора и обработки информации совместно с СТЭ могут быть представлены в виде замкнутой неоднородной сети массового обслуживания, состоящей из K = R + M систем массового обслуживания (СМО), где СМОk (![]() ) описывают процессы появления заявок на ремонт, а остальные М СМО имитируют процессы функционирования ремонтного органа по удовлетворению этих заявок. Каждый ремонтный орган силами входящих в его состав бригад обслуживает одно из подмножеств элементов системы. При этом в общем случае эти подмножества могут быть пересекающимися, т.е. определённые элементы системы могут быть обслужены силами либо одного, либо другого ремонтного органа.
) описывают процессы появления заявок на ремонт, а остальные М СМО имитируют процессы функционирования ремонтного органа по удовлетворению этих заявок. Каждый ремонтный орган силами входящих в его состав бригад обслуживает одно из подмножеств элементов системы. При этом в общем случае эти подмножества могут быть пересекающимися, т.е. определённые элементы системы могут быть обслужены силами либо одного, либо другого ремонтного органа.
Движение заявок по сети и распределение зон обслуживания определяются маршрутной матрицей Р = рlg (![]() ), где рlg – вероятность поступления заявки из СМОl в СМОg, а
), где рlg – вероятность поступления заявки из СМОl в СМОg, а ![]() (
(![]() ).
).
Состояние сети массового обслуживания определяется матрицей
![]() ,
,
где ![]() ,
,
а пmr – количество заявок класса r, находящихся в СМОm. Вероятность ![]() того, что сеть массового обслуживания находится в состоянии
того, что сеть массового обслуживания находится в состоянии ![]() в стационарном режиме определяется следующим образом [1]:
в стационарном режиме определяется следующим образом [1]:
![]() ,
,
где ![]() – нормализующая константа,
– нормализующая константа,
y – множество всех возможных состояний сети массового обслуживания.
Вид функции fk(nk*) определяется в зависимости от выбранной дисциплины обслуживания, характеристик потока заявок на обслуживание. При этом системы обслуживаемых элементов без резервирования, а также подсистемы элементов с нагруженным резервированием могут быть описаны системами массового обслуживания типа IS (тип СМО, где число обслуживающих приборов не меньше суммарного количества заявок), допускающими произвольное распределение наработки на отказ, но имеющими рациональное преобразование Лапласа (например, распределение Эрланга) [3].
Подсистемы элементов с ненагруженным или комбинированным резервом описываются СМО типа FCFS (тип СМО, в которых требования обслуживаются в порядке их поступления) с числом обслуживающих приборов, равным числу активно работающих элементов.
Распределение наработки на отказ допускается экспоненциальное. Функция fk(nk*) в этих случаях имеет следующий вид [1]:
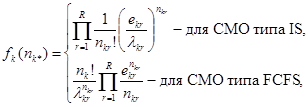
где еkr определяется из системы линейных уравнений
![]() , (1)
, (1)
a P(l,k)r – вероятность перехода заявки класса r из СМОl; в CMOk.
Величина lkr представляет собой среднюю интенсивность отказов на интервале Т между плановыми периодическими (техническими обслуживаниями) ТО для обслуживаемых средств r-го типа и определяется следующим образом:
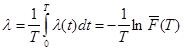 , (2)
, (2)
где ![]() – вероятность безотказной работы.
– вероятность безотказной работы.
Во многих случаях достаточно адекватным описанием реальных процессов отказов аппаратуры различных типов является описание распределения наработки на отказ при помощи закона Эрланга:
![]() ,
,
а интенсивность отказов является функцией времени:
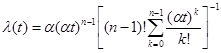 .
.
В этом случае средняя интенсивность lср(Т) на интервале Т между ТО определяется с учётом (1) и (2):
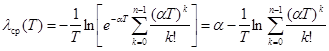 .
.
Обслуживание заявок на ремонт в CMOk (k = R + 1, K) может осуществляться в соответствии с дисциплинами FCFS, LCFS или RAND. Для СМО с дисциплинами FCFS допускается при этом экспоненциальное распределение времени обслуживания, для двух других дисциплин – произвольные с рациональными преобразованиями Лапласа и средними ![]() . При этом fk(nk*) определяется выражением [1]:
. При этом fk(nk*) определяется выражением [1]:
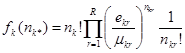 .
.
Результаты исследования и их обсуждение
Вероятность того, что любая совокупность средств, обслуживаемых ремонтными органами в произвольный момент времени, окажется в том или ином состоянии (например, в состоянии работоспособности), определяется как сумма вероятностей нахождения сети массового обслуживания во множестве всех таких состояний, в которых данное условие выполняется. Знание стационарных вероятностей нахождения сети массового обслуживания в любом из возможных состояний позволяет совместно с использованием логико-вероятностных методов произвести расчёт показателей готовности и временных показателей как для отдельных средств, так и для заданной совокупности средств.
Рассмотрим далее случай трёхуровневого восстановления. Данный случай имеет место, если восстановление работоспособности производится следующим образом. При отказе эксплуатирующий персонал производит локализацию неисправности и замену отказавшего блока на работоспособный из ЗИП (первый уровень восстановления). Отказавший блок отправляется в ремонтный орган (второй уровень восстановления), где производится устранение мелких и средних неисправностей. После устранения таких неисправностей отремонтированный блок возвращается либо туда же, откуда он поступил, либо к другому аналогичному средству в зависимости от потребности.
Если же неисправность имеет такую тяжесть, что она не может быть устранена силами ремонтного органа, либо если в данном органе отсутствуют необходимые для ремонта запасные элементы, к восстановлению работоспособности привлекается третий уровень системы ремонта – специализированная ремонтная организация.
Таким образом, с выхода ремонтного органа второго уровня в случае успешного завершения ремонта восстановленное устройство с вероятностью р1 возвращается в систему применения по назначению, либо, в противном случае, с вероятностью р2 = 1 – р1 данное устройство становится объектом для обслуживания силами специализированной ремонтной организации.
Данная сеть массового обслуживания содержит K = R + М1 + М2 систем массового обслуживания, где: СМОr (![]() ) описывают процессы наработки средств на отказ; CMO
) описывают процессы наработки средств на отказ; CMO![]() (m1 = R + 1, R + M1) имитируют процессы функционирования ремонтных органов второго уровня; СМО
(m1 = R + 1, R + M1) имитируют процессы функционирования ремонтных органов второго уровня; СМО![]() (т2 = R + М1 + 1, K) имитируют процессы функционирования специализированных ремонтных организаций.
(т2 = R + М1 + 1, K) имитируют процессы функционирования специализированных ремонтных организаций.
Выводы
В статье рассмотрены вопросы разработки математической модели функционирования системы технической эксплуатации распределенных информационных систем сбора и обработки информации. Модель базируется на основе совместного представления обслуживаемой распределенной системы сбора и обработки информации и системы ее технической эксплуатации в виде замкнутой неоднородной сети массового обслуживания. Сеть массового обслуживания включает системы массового обслуживания двух типов: моделирования процесса возникновения заявок на ремонт и моделирования процессов функционирования ремонтных органов по удовлетворению этих заявок. Знание стационарных вероятностей нахождения сети массового обслуживания в любом из возможных состояний позволяет совместно с использованием логико-вероятностных методов произвести расчёт показателей готовности и временных показателей как для отдельных средств, так и для заданной совокупности средств. Показано, что значение показателя надежности может быть получено в виде суммы вероятностей нахождения сети массового обслуживания во множестве состояний, в которых выполняется условие работоспособности для обслуживаемой системы. Рассмотрены варианты двухуровневой структуры системы технической эксплуатации «персонал – ремонтный орган» и трехуровневой структуры «персонал – ремонтный орган – специализированная ремонтная организация».
Рецензенты:
Козлов В.В., д.т.н., профессор, профессор кафедры ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского» Министерства обороны РФ, г. Санкт-Петербург.
Смагин В.А., д.т.н., профессор, профессор кафедры ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского» Министерства обороны РФ, г. Санкт-Петербург.



