Изменения, происходящие в обществе, и, как следствие, изменения в сфере высшего образования предъявляют новые требования к его результатам. Улучшение подготовки специалистов различных направлений невозможно без высокого уровня математической подготовки. Поэтому важной составной частью повышения качества обучения является совершенствование методов обучения, которые обеспечивают глубокое и прочное усвоение знаний и умений.
Эффективность обучения во многом зависит от отбора, конструирования, организации системы задач (упражнений). Хорошо известно, что в истории использования задач в обучении математике в зависимости от целей обучения математике, содержания математического образования, функций обучения математике выделяются следующие этапы:
1) изучение математики с целью обучения решению задач;
2) изучение математики, сопровождающееся решением задач;
3) обучение математике через решение задач.
Различным аспектам роли и месту задач в обучении математике посвящены работы С.Б. Суворова, К.И. Нешкова, А.Д. Семушина, Я.И. Груденова, М.Р. Леонтьева, Г.И. Саранцева и др.
Каждый этап характеризуется различными требованиями к применению задач в обучении математике. В настоящее время функции задач в обучении математике расширяются, они являются средством математического образования. Задачи играют роль многоаспектного явления и выступают в качестве:
- носителя действий, адекватных содержанию обучения математике;
- средства целенаправленного формирования знаний, умений и навыков;
- способа организации и управления учебно-познавательной деятельности учащихся;
- одной из форм реализации методов обучения;
- средства связи теории с практикой. [4]
Велика роль задач в профессиональной направленности математической подготовки студентов инженерно-строительных специальностей. Задачи выступают основным средством формирования качеств личности, необходимых для выполнения основных видов профессиональной деятельности.
Переходя к понятию профессионально ориентированной задачи в строительстве, заметим, что в качестве задачной ситуации в ней выступает некая модель профессиональной ситуации, в которой по известным характеристикам профессионального объекта или явления надо найти другие его характеристики или свойства. Разрешение или исследование представленной профессиональной ситуации способствует развитию у субъекта определенных профессиональных качеств.
Таким образом, профессионально ориентированная математическая задача – это задача, условие и требование которой определяют собой модель некоторой ситуации, возникающей в профессиональной деятельности инженера-строителя, а исследование этой ситуации средствами математики способствует профессиональному развитию личности студента.
Вышесказанное позволяет нам сформулировать требования, предъявляемые к профессионально ориентированным задачам, используемым в рамках математической подготовки будущего строителя:
1) задача должна описывать ситуацию, возникающую в профессиональной деятельности инженера-строителя;
2) в задаче должны быть неизвестны характеристики некоторого профессионального объекта или явления, которые надо исследовать субъекту по имеющимся известным характеристикам с помощью средств математики;
3) решение задач должно способствовать прочному усвоению математических знаний, приемов и методов, являющихся основой профессиональной деятельности инженера- строителя;
4) задачи должны обеспечить усвоение взаимосвязи математики с общетехническими и специальными дисциплинами;
5) содержание задачи и ее решение требуют знаний по специальным предметам;
6) содержание профессионально ориентированной математической задачи определяет пропедевтический этап изучения понятий специальных дисциплин;
7) решение задач должно обеспечивать математическое и профессиональное развитие личности инженера-строителя.
Приведем примеры профессионально ориентированных задач, в которых используется математический аппарат:
1. При разработке гипсового композита исследовалось влияние на плотность ![]() , в сухом состоянии введения вспученного перлитового песка в количестве от 0 до
, в сухом состоянии введения вспученного перлитового песка в количестве от 0 до ![]() от массы гипса при формировании изделий из технологической смеси нормальной густоты (по Суттарду). При гипотезе линейного снижения
от массы гипса при формировании изделий из технологической смеси нормальной густоты (по Суттарду). При гипотезе линейного снижения ![]() в зависимости от нормализованного фактора
в зависимости от нормализованного фактора ![]() нужно найти две оценки МНК в модели
нужно найти две оценки МНК в модели ![]() по результатам пяти опытов, представленных в таблице.
по результатам пяти опытов, представленных в таблице.
|
|
-1 |
-0,5 |
0 |
0,5 |
1 |
|
|
1228 |
1136 |
1120 |
1044 |
942 |
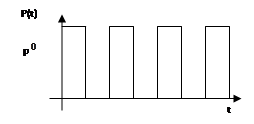
2. Представьте в виде тригонометрического ряда периодические изменения нагрузки с равными периодами действия, показанными на рисунке. Функция нагрузки задана следующим образом:
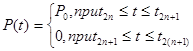
При этом ![]()
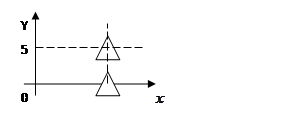
3. С помощью подъемного крана извлекают железобетонную надолбу со дна реки глубиной 5 м. Какая работа при этом совершается, если надолба имеет форму правильного тетраэдра с ребром 1 м. (плотность железобетона 2500 кг/![]() , плотность воды 1000 кг/
, плотность воды 1000 кг/![]() )?
)?
Технология формирования профессиональных качеств личности посредством задач включает в себя анализ основных дидактических единиц темы и разработку совокупности профессионально ориентированных математических задач, решение которых позволяет сделать вывод о сформированности профессионально значимых качеств личности.
На примере темы «Обыкновенные дифференциальные уравнения» покажем задачи, способствующие формированию профессиональных качеств личности.
Анализ программы по теме «Обыкновенны дифференциальные уравнения» позволяет выделить такие дидактические единицы темы, как: дифференциальное уравнение и его порядок; общее и частное решение уравнения; интегральная кривая; типы дифференциальных уравнений и соответствующие им методы решения. Задачи различных учебных пособий можно разделить на три группы, выделяя в каждой из них основные.
Первая группа – это группа, состоящая из задач, связанных с процессами выделения тепла.
Задача 1. Интенсивность тепловыделения бетона ![]() пропорциональна не выделившемуся к данному моменту времени количеству тепла:
пропорциональна не выделившемуся к данному моменту времени количеству тепла: ![]() , где
, где ![]() – максимальное количество тепла, которое может выделиться в бетоне данного состава при полной гидратации цемента,
– максимальное количество тепла, которое может выделиться в бетоне данного состава при полной гидратации цемента, ![]() – параметр, зависящий от типа цемента (для бетонов на портландцементе он изменяется в пределах от 0,010 – 0,015 1/ч). Определить функцию интенсивности тепловыделения бетона.
– параметр, зависящий от типа цемента (для бетонов на портландцементе он изменяется в пределах от 0,010 – 0,015 1/ч). Определить функцию интенсивности тепловыделения бетона.
Задача 2. По закону Ньютона скорость охлаждения какого-либо тела в воздухе пропорциональна разности между температурой тела и температурой воздуха: ![]() . В комнате, где температура воздуха
. В комнате, где температура воздуха ![]() С, кирпич остывает за 20 мин. со
С, кирпич остывает за 20 мин. со ![]() до
до ![]() . Найти закон охлаждения кирпича; через сколько времени температура вынутого из печи кирпича понизится до
. Найти закон охлаждения кирпича; через сколько времени температура вынутого из печи кирпича понизится до ![]() ? Повышением температуры в комнате пренебречь.
? Повышением температуры в комнате пренебречь.
Вторая группа содержит задачи на исследование деформации строительных сооружений и колебательных процессов, происходящих в строительных конструкциях.
Задача 1. Балка (с модулем упругости Е и моментом инерции J) наглухо заделана в конце О и подвергается действию сосредоточенной вертикальной силы Р, приложенной к концу балки L на расстоянии l от места закрепления (рис. 1). Определить прогиб балки h на конце балки L.
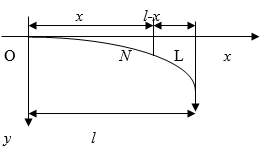
Рис. 1
Задача 2. Дифференциальное уравнение ![]()
![]() описывает свободные колебательные процессы в строительных конструкциях. Решением данного уравнения являются интегральные кривые (рис. 2):
описывает свободные колебательные процессы в строительных конструкциях. Решением данного уравнения являются интегральные кривые (рис. 2):
а) при ![]() б) при
б) при ![]() в) при
в) при ![]()
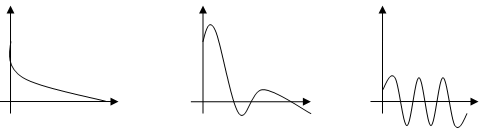
Рис. 2
Исследовать поведение интегральной кривой при ![]() и определить характер колебаний.
и определить характер колебаний.
Третья группа состоит из задач, в которых рассматривается скорость протекания процессов.
Задача 1. Машина перевозит щебень с места добычи до места назначения со скоростью ν![]() . Зная, что
. Зная, что ![]() ν(t), определить, через сколько времени машина доедет до места назначения, если расстояние между пунктами равно S.
ν(t), определить, через сколько времени машина доедет до места назначения, если расстояние между пунктами равно S.
Задача 2. Свободно висящий на крюке строительного крана канат соскальзывает с него под действием силы тяжести (трением можно пренебречь). Определить, за какое время соскользнет с крюка весь канат, если в начальный момент канат покоился, а длина каната с одной стороны крюка была равна 10 м, с другой – 8 м.
Выделенные ключевые задачи по теме «Дифференциальные уравнения» позволяют формировать следующие умения:
- определение изменения температур математическими методами;
- исследование деформации строительной конструкции с помощью математических расчетов;
- исследование колебательных процессов, происходящих в строительных конструкциях;
- применение методов решения дифференциальных уравнений к исследованию различных процессов;
- представление о взаимосвязи методов решения дифференциальных уравнений с дисциплинами специализации.
Правильное решение одной профессионально ориентированной задачи не корректно считать свидетельством сформированности профессиональных умений. Только систематическое и целенаправленное применение задач профессионального содержания на аудиторных занятиях (лекции, практические занятия) и внеаудиторных (подготовка докладов и рефератов на заданную тему, выполнение расчетных, курсовых работ) служит средством формирования профессионально значимых качеств личности.
На примере рассмотренной ниже задачи нам хотелось бы подчеркнуть значимость математики в профессиональной деятельности будущих строителей. Для ее решения студент должен обладать:
- определенным уровнем сформированности профессионального умения, а именно, умения определять распределение в строительных изделиях математическими методами;
- иллюстрации связей раздела «Уравнения математической физики» с дисциплиной специализации «Конструкции из дерева и пластмасс»;
- развитием профессиональной мотивации при изучении данного раздела математики.
Задача. Одна из граней длинного прямоугольного бруса (рис. 3) поддерживается при заданной температуре, на остальных гранях Т=0. Найти установившуюся температуру в произвольной точке внутри бруса [3].
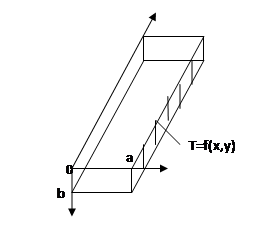
Рис.3
На основе анализа решения задачи составляется математическая модель задачи в виде уравнения теплопроводности:
![]() ,
,
удовлетворяющего двум парам краевых условий:
![]()
![]()
![]()
![]() .
.
Применяя метод Фурье к решению данного уравнения, студенты находят функцию
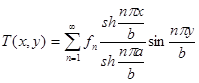 , где
, где 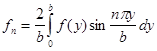 , определяющую установившуюся температуру в произвольной точке внутри бруса.
, определяющую установившуюся температуру в произвольной точке внутри бруса.
Анализ решения задачи позволяет определить уровень сформированности профессиональных качеств личности инженера-строителя: профессиональной мотивации, взаимосвязи математики (в частности уравнения теплопроводности и его решения методом Фурье) со строительной дисциплиной «Конструкции из дерева и пластмассы», умения определять распределение температур в строительных изделиях математическими методами.
Практика преподавания в строительном университете показывает, что процесс обучения организованный с позиции системного представления профессиональной направленности математической подготовки студентов формирует профессиональные качества личности: понимание взаимосвязи содержания математического образования с содержанием дисциплин специализации, профессиональное мышление, понимание роли математических знаний и умений для профессионального развития личности.
Профессионально ориентированные задачи можно использовать в практике преподавания математики для различных направлений подготовки студентов. Отличие заключается в системе задач профессионального содержания, так как деление задач на группы и выделение в каждой из них ключевых обуславливается спецификой профессионального направления.
Рецензенты:
Усманов В.В., д.п.н., профессор, первый проректор, проректор по научной работе, ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза.
Гарькина И.А., д.т.н., профессор, профессор кафедры «Математики и математического моделирования», ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза.



