Введение
При движении амфибийной транспортной машины с аэродинамическим движителем по пересеченной местности на несущие элементы ее конструкции действуют гироскопические моменты, возникающие вследствие изменения плоскости вращения воздушного винта, представляющего собой гироскоп с большими вращательными импульсами.
Эти моменты необходимо учитывать, особенно при расчете вала воздушного винта, возможность поломки которого должна быть полностью исключена.
Двухлопастной воздушный винт, по сути, представляет co6ой быстрый несимметричный уравновешенный гироскоп. Теория несимметричного уравновешенного гироскопа хорошо изучена в приложении к динамике полета летательных аппаратов [1].
Однако условия эксплуатации наземных транспортных машин с аэродинамическими движителями, особенно при движении по пересеченной местности и при преодолении препятствий в виде снежных валов, торосистых льдов, насыпей, пней и прочего резко отличаются от условий эксплуатации самолетов.
Таким образом, определение и учет гироскопических моментов для наземных машин имеют свои особенности и требуют углубленного изучения.
Цель исследования
Предложить подходы к определению гироскопических моментов, действующих на вал винта наземных амфибийных транспортных машин с аэродинамическими движителями.
Материал и методы исследования
Для определения гироскопического момента воспользуемся формулами [1]:
,
, (1)
,
где 
– угол поворота винта в принятой системе отсчета;
– угловая скорость винта;
– угловая скорость движущейся амфибийной транспортной машины с аэродинамическим движителем;
– угол между векторами 
и 
;
– осевой момент инерции винта;
и 
– главные центральные моменты инерции винта;
– значения составляющих гироскопического момента.
Введя собственный вращательный импульс винта 
, можно придать формулам (1) вид:
,
, (2)
.
Анализируя формулы (2), можно заметить следующее.
Главная составляющая гироскопического момента 
не сохраняет постоянного значения при постоянных и , так как зависит от угла . Вместе с изменением угла она периодически изменяется в пределах 
. При этом частота этих изменений в 2 paза больше собственной угловой скорости винта , равной 
. Поскольку для тел, имеющих форму стержня, 
и 
, то составляющая изменяется периодически приблизительно от нуля до 
, то есть колеблется около среднего значения 
.
Кроме главной составляющей гироскопический момент двухлопастного винта имеет составляющую 
, перпендикулярную и изменяющуюся между значениями 
с частотой, также в 2 раза большей собственной угловой скорости винта . Следовательно, величина вектора изменяется приблизительно между 
.
Гироскопический момент имеет составляющую 
, направленную вдоль оси винта и пульсирующего также с частотой 
. Эту составляющую можно не учитывать, так как ее влияние ничтожно мало по сравнению с влиянием неравномерности работы двигателя.
Направления векторов , и соответствующих им сил 
, 
, 
, 
определяются следующим образом.
Составляющая гироскопического момента стремится кратчайшим путем совместить векторы и угловых скоростей вращения винта и транспортной машины.
На рисунке 1а направлениям и соответствуют вращения винта по часовой стрелке (если смотреть со стороны кормы) и транспортной машины при подъеме носовой части.
Направления вектора и соответствующей ему пары сил и показаны на рисунке 1б. Поскольку величина пульсирует от нуля до с частотой , то и величины сил и пульсируют с той же частотой.
На рисунке 1в показана схема вектора и соответствующей ему пары сил и . Поскольку колеблется между значениями , то и соответствующие ему силы и меняют свои направления.
На рисунке 1в сплошными векторами изображены , , , соответствующие их наибольшим значениям, получаемым при 
; противоположные им векторы при 
изображены пунктирными линиями.
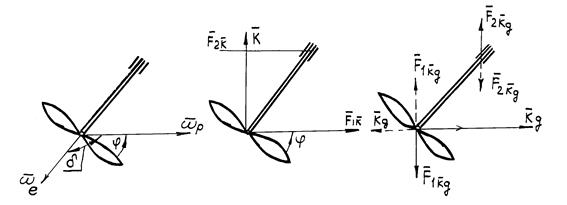
а) б) в)
Рисунок 1. Схема направлений векторов , и соответствующих им пар сил
Поскольку 
, то значение их результирующей 
при 
составляет:
,
, (3)
Если принять начало вектора за полюс, то угол 
между полярной осью и вектором , отсчитываемый по часовой стрелке, находится по формуле:
. (4)
Осевой момент инерции , необходимый для вычисления 
, определяется соотношением:
,
где 
– радиус винта, 
– масса винта.
Результаты исследования и их обсуждение
Анализ выражения (4) показывает, что если винт повернется на такой угол (по часовой стрелке), сторона которого находится в четвертой или первой четвертях, то для нахождения направления , соответствующего этому углу , нужно сторону угла повернуть по часовой стрелке на 320°. При повороте же винта на угол , сторона которого находится в третьей и второй четвертях, для нахождения направления сторону угла надо повернуть по часовой стрелке на 90°. Изменяясь, вектор своим концом описывает кривую, изображенную на рисунке 2.
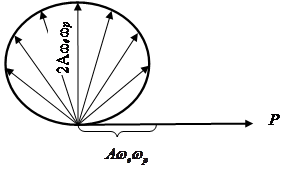
Рисунок 2. Изменение вращения вектора
Направление вращения вектора происходит по часовой стрелке (это также следует из анализа равенства 
.).
Выводы или заключение
При наличии значений 
, входящих в соотношение (3), могут быть найдены численные величины гироскопического момента и закон его изменения при любой смене направления движения амфибийной транспортной машины с аэродинамическим движителем в различных координатных плоскостях (движение по неровностям, на поворотах и др.).
По результатам анализа могут быть выявлены наиболее неблагоприятные режимы движения, ведущие к возникновению наибольших гироскопических моментов.
Рецензенты:
Полянин И.А., д.т.н., профессор, заведующий кафедрой транспортно-технологических машин, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Поволжский государственный технологический университет» (Министерство образования и науки Российской Федерации), г. Йошкар-Ола.
Наводнов В.Г., д.т.н., профессор, заведующий кафедрой прикладной математики и информационных технологий, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Поволжский государственный технологический университет» (Министерство образования и науки Российской Федерации), г. Йошкар-Ола.
Лубенцов В.Ф., д.т.н., профессор, зам. директора по научной работе, профессор кафедры «Информационные системы, Электропривод и автоматика» Невинномысский технологический институт ГОУ ВПО «Северо-Кавказский государственный технический университет», г. Невинномысск.