Введение
Шифрование информации имеет давнюю историю. Первые методы шифрования применялись узким кругом лиц в основном для сохранения военной или коммерческой тайны. Свои собственные шифры часто использовали государственные деятели и дипломаты для личной переписки. Методы шифрования держали в строжайшем секрете.
В наши дни благодаря совершенствованию вычислительной техники и развитию математических методов обработки информации многие старые шифры оказались ненадежными. Сегодня алгоритмы шифрования открыто публикуются и обсуждаются специалистами. Однако знание шифрующего алгоритма мало чем может помочь злоумышленнику, решившему расшифровать перехваченное сообщение. Дело в том, что современные методы шифрования, как правило, используют секретный ключ, без знания которого расшифровать зашифрованный текст крайне затруднительно. Поэтому основная сложность вскрытия такого шифра заключается в нахождении секретного ключа [4].
Генетические алгоритмы первоначально возникли для поиска экстремальных значений функций, заданных на ограниченных областях в многомерных пространствах [2]. Затем сферу их применения удалось расширить на задачи комбинаторной оптимизации со сложными, трудноформализуемыми функционалами. Например, в [5] генетический алгоритм успешно применен для нахождения секретного ключа блочного перестановочного шифра. Секретным ключом здесь является случайная перестановка чисел 1,2,3,…,n. Подстановочный шифр Тритемия-Белазо-Виженера (ТБВ-шифр) обладает более сложным секретным ключом, состоящим из двухнезависимых символьных строк. Первая строка – это ключевое слово, а вторая – произвольная перестановка букв алфавита. Теоретически обе части ключа можно было бы найти перебором всех вариантов, однако на практике осуществить полный перебор за разумное время невозможно, т.к. пространство поиска слишком велико. Поэтому вполне оправданным в данной ситуации становится использование генетического алгоритма как одного из методов направленного ограниченного поиска.
Описание шифра Тритемия – Белазо – Виженера
Секретный ключ в ТБВ-шифре состоит из двух частей. Первая часть – это произвольное ключевое слово, например, «гдежевий». Чем оно длиннее, тем сложнее «взломать» шифр. Вторая часть секретного ключа представляет собой перемешанный в произвольном порядке русский алфавит. Она же является первой строкой в квадратной таблице – таблице Виженера. Каждая следующая строка этой таблицы получается циклическим сдвигом предыдущей строки на одну позицию влево. Исключение составляют нулевая (верхняя) строка и нулевой (крайний левый) столбец таблицы Виженера – в них буквы алфавита записаны в правильном порядке. Первые 11 строк таблицы Виженера могут выглядеть, например, как показано на рис. 1.
|
|
А |
Б |
В |
Г |
Д |
Е |
Ж |
З |
И |
Й |
К |
Л |
М |
Н |
О |
П |
Р |
С |
Т |
У |
Ф |
Х |
Ц |
Ч |
Ш |
Щ |
Ъ |
Ы |
Ь |
Э |
Ю |
Я |
|
А |
Е |
Ш |
А |
Х |
Ж |
З |
Т |
Э |
М |
Щ |
И |
Л |
Ч |
Ъ |
Я |
Ы |
В |
Д |
Й |
Ь |
Г |
Ц |
У |
Н |
С |
О |
Ю |
Б |
Ф |
Р |
К |
П |
|
Б |
Ш |
А |
Х |
Ж |
З |
Т |
Э |
М |
Щ |
И |
Л |
Ч |
Ъ |
Я |
Ы |
В |
Д |
Й |
Ь |
Г |
Ц |
У |
Н |
С |
О |
Ю |
Б |
Ф |
Р |
К |
П |
Е |
|
В |
А |
Х |
Ж |
З |
Т |
Э |
М |
Щ |
И |
Л |
Ч |
Ъ |
Я |
Ы |
В |
Д |
Й |
Ь |
Г |
Ц |
У |
Н |
С |
О |
Ю |
Б |
Ф |
Р |
К |
П |
Е |
Ш |
|
Г |
Х |
Ж |
З |
Т |
Э |
М |
Щ |
И |
Л |
Ч |
Ъ |
Я |
Ы |
В |
Д |
Й |
Ь |
Г |
Ц |
У |
Н |
С |
О |
Ю |
Б |
Ф |
Р |
К |
П |
Е |
Ш |
А |
|
Д |
Ж |
З |
Т |
Э |
М |
Щ |
И |
Л |
Ч |
Ъ |
Я |
Ы |
В |
Д |
Й |
Ь |
Г |
Ц |
У |
Н |
С |
О |
Ю |
Б |
Ф |
Р |
К |
П |
Е |
Ш |
А |
Х |
|
Е |
З |
Т |
Э |
М |
Щ |
И |
Л |
Ч |
Ъ |
Я |
Ы |
В |
Д |
Й |
Ь |
Г |
Ц |
У |
Н |
С |
О |
Ю |
Б |
Ф |
Р |
К |
П |
Е |
Ш |
А |
Х |
Ж |
|
Ж |
Т |
Э |
М |
Щ |
И |
Л |
Ч |
Ъ |
Я |
Ы |
В |
Д |
Й |
Ь |
Г |
Ц |
У |
Н |
С |
О |
Ю |
Б |
Ф |
Р |
К |
П |
Е |
Ш |
А |
Х |
Ж |
З |
|
З |
Э |
М |
Щ |
И |
Л |
Ч |
Ъ |
Я |
Ы |
В |
Д |
Й |
Ь |
Г |
Ц |
У |
Н |
С |
О |
Ю |
Б |
Ф |
Р |
К |
П |
Е |
Ш |
А |
Х |
Ж |
З |
Т |
|
И |
М |
Щ |
И |
Л |
Ч |
Ъ |
Я |
Ы |
В |
Д |
Й |
Ь |
Г |
Ц |
У |
Н |
С |
О |
Ю |
Б |
Ф |
Р |
К |
П |
Е |
Ш |
А |
Х |
Ж |
З |
Т |
Э |
|
Й |
Щ |
И |
Л |
Ч |
Ъ |
Я |
Ы |
В |
Д |
Й |
Ь |
Г |
Ц |
У |
Н |
С |
О |
Ю |
Б |
Ф |
Р |
К |
П |
Е |
Ш |
А |
Х |
Ж |
З |
Т |
Э |
М |
Рис. 1. Первые одиннадцать строк таблицы Виженера
Будем считать, что в таблице Виженера каждый столбец (кроме нулевого) и каждая строка (кроме нулевой) помечены определенной буквой. Например, третий столбец таблицы, изображенной на рис. 1, помечен буквой «В», а пятая строка – буквой «Д». Зашифруем, например, текст «БЕЛЫЙ МЕДВЕДЬ САМЫЙ КРУПНЫЙ ХИЩНИК» при помощи ключевого слова «ГДЕЖЕВИЙ» и таблицы Виженера (см. рис.1). Шифрование выполняется побуквенно. Первые буквы исходного текста и ключевого слова – это «Б» и «Г». Находим в таблице столбец, помеченный буквой «Б», и строку, помеченную буквой «Г» (это второй столбец и четвертая строка). На их пересечении расположена буква «Ж», следовательно, она и будет первой буквой зашифрованного текста. Аналогично «вычисляем» вторую букву зашифрованного текста. Это будет буква «Щ», потому что она расположена на пересечении столбца, помеченного буквой «Е», и строки, помеченной буквой «Д» (буквы «Е» и «Д» – это соответственно вторые буквы исходного текста и ключевого слова). Продолжая аналогичным образом процесс шифрования, получим зашифрованный текст «ЖЩВШЯ ЯЪЪЗЩЩА УАГЖЧ ЯЦОГЫХЙ СЧКЬЪЧ». Расшифровать этот текст, зная ключевое слово и таблицу Виженера, не составляет труда.
Важно отметить, что ТБВ-шифр относится к классу полиалфавитных шифров замены, поскольку одна и та же буква исходного текста при шифровании может быть заменена разными буквами. Например, в данном случае буква «Ы» была заменена сначала на «Ш», потом на «Ж», а затем на «Х». Это обстоятельство усложняет процесс расшифрования посредством простого частотного криптоанализа. Тем не менее расшифрование возможно, если воспользоваться тестом Ф. Казиски или индексом совпадения У. Фридмана [1].
Постановка задачи
Предположим, что мы имеем шифр-текст, т.е. текст, зашифрованный с помощью ТБВ-шифра, секретный ключ которого нам не известен. Тем не менее мы хотим расшифровать этот шифр-текст, т.е. получить исходный текст. Будем считать, что исходный текст являлся осмысленным, составленным из грамотно написанных слов русского языка. Требования «осмысленности» и «грамотности» не случайны. Известно, что частота встречаемости каждой буквы алфавита в достаточно длинном осмысленном, грамотно написанном тексте – величина почти предсказуемая. И чем длиннее текст, тем она ближе к известной среднестатистической частоте. Например, буква «О» имеет среднестатистическую частоту встречаемости 0,09, а буква «Ф» – 0,002 [4]. Иными словами, в произвольном осмысленном тексте, написанном на русском языке, среди тысячи подряд идущих символов (включая «пробел») буква «О» встретится примерно 90 раз, а буква «Ф» – примерно 2 раза.
Анализ ТБВ-шифра показывает, что один и тот же шифр-текст можно получить с помощью двух разных ключевых слов и двух разных соответствующих им таблиц Виженера. Задача дешифрования считается решенной, если мы найдем какое-либо ключевое слово и соответствующую ему таблицу Виженера, с помощью которых правильно (или почти правильно) расшифровывается заданный шифр-текст. Текст будем считать почти правильно расшифрованным, если его смысл понятен, хотя отдельные слова в нем содержат ошибки. Например, в одном из тестовых заданий шифр-текст имел длину около 25 тыс. символов. В результате работы генетического алгоритма был получен почти правильно расшифрованный текст (см. рис. 2).
БЫЛ_ХОЛЬДНЫЙ_ЯСНЫЙНАПРЕЛЬСКИЙНДЕНЬ_И_ЧАСИ_ПРОБИЛИ_ТЮИНАДЦАТЬ_У_КНУВ_ ПОДБОЮОДОК_В_ГРУТЬ_ЧТОБЫ_СПОСТИСЬ_ОТ_ЗЩОГО_ВЕТРА_АИНСТОН_СМИ_ ТОРОПЛИВОНШМЫГНУЛ_ЗАНСТЕКЛЯННУЮНДВЕРЬ_ЖИЛОСО_ДОМА_…
Рис. 2. Начальный фрагмент почти правильно расшифрованного текста
Как видим, в тексте есть много правильно написанных слов («был», «ясный», «апрельский»), но также встречаются и слова с ошибками («хольдный», «часи», «тюинадцать»). Исправить все ошибки удалось вручную, не меняя при этом найденное ключевое слово, а лишь переставив буквы «Б» и «Е» во второй строке таблицы Виженера «ЕШАХЖЗТЭМЩИЛЧЪЯЫВДЙЬГЦУНСОЮБ_ФРКП».
Описание генетического алгоритма
Без знания таблицы Виженера и ключевого слова процесс дешифрования будет состоять из двух этапов: сначала мы найдем длину ключевого слова, а затем уже само это слово и таблицу Виженера. Генетический алгоритм будет использоваться только на втором этапе, причем для построения таблицы Виженера достаточно лишь найти первую её строку, поскольку все последующие строки получаются из второй циклическим сдвигом, а нулевая строка содержит все буквы алфавита в правильном порядке (см. рис. 1).
Длину ключевого слова можно определить с помощью простого частотного анализа, примененного к специально выбранным позициям шифр-текста [4]. Как известно, в тексте, зашифрованном с помощью ТБВ-шифра, распределение частот букв близко к равномерному. Однако если из шифр-текста извлечь последовательность символов, стоящих на позициях с номерами 1, 1 + L, 1 + 2L, 1 + 3L и т.д., где L – это длина ключевого слова, то в этой подпоследовательности частоты встречаемости букв алфавита будут близки к заранее известным среднестатистическим значениям. Учитывая этот факт, нужно исследовать функцию
![]() ,
,
где N – количество букв в алфавите, ej – среднестатистическая (эталонная) частота встречаемости j-й буквы алфавита, fj(i) – частота j-й буквы в подпоследовательности символов шифр-текста, стоящих на позициях с номерами i, i + L, i + 2L,…, i + kL. Функция S(L) позволяет найти длину ключевого слова, однако никакой информации о самом слове не дает. Действительно, перебирая натуральные значения L от 2 до некоторого разумного порога MaxL, найдем первый локальный минимум функции S(L). Как показывают многочисленные эксперименты, найденная таким образом точка минимума L0 является искомой длиной ключевого слова, а значение функции S(L0) составляет примерно 25–30 % от ближайших значений S(L0 – 1) и S(L0 + 1). Наилучшие результаты достигаются, когда длина шифр-текста на порядок превосходит длину ключевого слова.
Пусть в результате простого частотного анализа, примененного к L различным подпоследовательностям символов шифр-текста, стоящих на позициях с номерами i, i + L, i + 2L,i + 3L и т.д., где i = 1, 2, 3, …, L, мы получили L перестановок букв алфавита. Обозначим их через π1, π2, π3,…, πL. Установить взаимно-однозначное соответствие между буквами алфавита и буквами указанных перестановок можно, например, выполнив сортировку букв по убыванию частот их встречаемости. Если перестановки π1, π2, π3,…, πL получаются друг из друга циклическим сдвигом, то любую из них можно считать первой строкой таблицы Виженера. После этого однозначно определится ключевое слово. Действительно, нулевая строка таблицы содержит все буквы алфавита в правильном порядке. Поэтому для построения остальной части таблицы достаточно найти лишь её первую строку (т.е. секретную перестановку букв алфавита), тогда все последующие строки получатся из первой циклическим сдвигом. Далее, поскольку каждый символ ключевого слова помечает какую-то одну строку таблицы Виженера, то само ключевое слово показывает, какие её строки и в какой последовательности использовались при шифровании. Пусть, например, для простоты алфавит содержит 5 букв: А,Б,В,Г,Д. Предположим, что ключевое слово имеет длину 4, и мы в результате предварительного частотного анализа получили следующие 4 перестановки букв алфавита: БАДВГ,ДВГБА,ГБАДВ, ВГБАД. Нетрудно видеть, что все они получаются друг из друга циклическими сдвигами. Поэтому, если в качестве первой строки таблицы Виженера выбрать перестановку БАДВГ, то получим следующую таблицу Виженера (см. рис. 3).
|
|
А |
Б |
В |
Г |
Д |
|
А |
Б |
А |
Д |
В |
Г |
|
Б |
А |
Д |
В |
Г |
Б |
|
В |
Д |
В |
Г |
Б |
А |
|
Г |
В |
Г |
Б |
А |
Д |
|
Д |
Г |
Б |
А |
Д |
В |
Рис. 3. Таблица Виженера для пятибуквенного алфавита А,Б,В,Г,Д
Соответствующим ей ключевым словом будет «АВДГ». Если же в качестве первой строки таблицы Виженера выбрать перестановку ВГБАД, то мы получим ключевое слово «ВДБА». Однако на результат расшифровки это никак не повлияет.
Иногда из-за ошибок частотного анализа не все L перестановок π1, π2, π3,…, πL получаются друг из друга циклическим сдвигом. Такое возможно, когда длина шифр-текста не слишком сильно превосходит длину ключевого слова. В этом случае для нахождения ключевого слова и таблицы Виженера будем использовать генетический алгоритм.
Таким образом, на вход генетическому алгоритму мы подаем L перестановок π1, π2,π3,…, πL, причем некоторые из них не получаются друг из друга за счет циклических сдвигов. Определим расстояние ρ(π',π'') между двумя перестановками π'иπ'' как число позиций, в которых они отличаются. Например, расстояние между перестановками АБВГД и БВАГД равно 3.
Цель генетического алгоритма – получить перестановку, которая больше всего похожа на какую-либо из строк таблицы Виженера. Заметим, что итоговая перестановка, вообще говоря, не обязана совпадать ни с одной из перестановок π1, π2, π3,…, πL. Однако расстояние между итоговой перестановкой и одной из строк таблицы Виженера в идеальном случае должно быть равно нулю.
Зафиксируем перестановку π1, а перестановку π2 сдвинем циклически так, чтобы расстояние ρ(π1,π2*) между π1 и перестановкой π2*, полученной из π2, было минимально возможным. Теперь перестановку π3 циклически сдвинем так, чтобы минимально возможной оказалась сумма расстояний ρ(π1,π3*)+ ρ(π2*,π3*), где перестановка π3* получается из π3 циклическим сдвигом. Продолжая аналогичный процесс циклических преобразований остальных перестановок, получим последовательность π1, π2*, π3*,…, πL*, в которой для каждого i = 2, 3, …, L перестановка πi* получается из πi с помощью таких циклических сдвигов, чтобы сумма ρ(π1,πi*)+ ρ(π2*,πi*)+ …+ ρ(πi – 1*,πi*) была минимально возможной. Тогда итоговая перестановка π** получается по принципу «голосования», т.е. для каждого i = 1, 2, 3, …, L на i –й позиции перестановки π**стоит буква, которая чаще всего встречалась в i –й позиции перестановок π 1, π2*, π3*,…, πL*. При возникновении конфликтных ситуаций принимаем любое допустимое решение.
Рассмотрим пример построения итоговой перестановки. Пусть в результате предварительного частотного анализа шифр-текста, написанного в алфавите А,Б,В,Г,Д и зашифрованного с помощью ключевого слова длины 4, получили следующие перестановки букв алфавита: π1 = БАДВГ,π2 = АДВГБ,π3 = ДВАБГ,π4 = ГВБАД. Перестановка π2 получается из π1 циклическим сдвигом на одну позицию влево. Однако перестановки π3 и π4 не получаются циклическим сдвигом ни друг из друга, ни из перестановок π1 и π2. Это свидетельствует об ошибках, допущенных при частотном анализе шифр-текста. Несмотря на это, у нас есть шанс получить правильную итоговую перестановку. Применив описанную выше процедуру построения последовательности π1, π2*, π3*, π4*, получим набор перестановок: БАДВГ, БАДВГ, БГДВА, БАДГВ. По итогам «голосования» искомая перестановка итоговая π** будет иметь вид БАДВГ, что позволяет нам получить таблицу Виженера, которая в данном примере в точности совпадает с таблицей, изображенной на рис. 3. Этой таблице соответствует ключевое слово «АБВГ», поскольку π1 совпала с первой строкой таблицы, π2 – со второй, π3 больше всего похожа на третью строку (т.к. получается из неё перестановкой букв «Г» и «А»), а π4 больше всего напоминает четвертую строку (т.к. получается из неё перестановкой букв «В» и «Г»).
К сожалению, нет никаких гарантий, что в рассмотренном выше примере итоговая перестановка π** является правильной. Возможно, нам не удастся правильно расшифровать шифр-текст с её помощью. Чтобы увеличить наши шансы, можно запустить описанную выше процедуру построения последовательности π1, π2*, π3*,…, πL* не только для возрастающей перестановки индексов 1, 2, 3,…, L, но и для всех остальных перестановок i1, i2, i3,…, iL. В этом случае итоговая перестановка π** будет являться строкой таблицы Виженера с номером i1. Поскольку при больших L исследовать все L! перестановок i1, i2, i3,…, iL за разумное время, то имеет смысл искать «наилучшую» из них с помощью генетического алгоритма. Можно воспользоваться естественным кодированием, т.е. перестановку i1, i2, i3,…, iL кодировать вектором (i1, i2, i3,…, iL). Это позволяет в дальнейшем применить стандартные операторы скрещивания и мутации [2]. Фитнесс-функцию будем вычислять по формуле
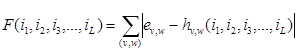 , (1)
, (1)
где суммирование ведется по всем двухбуквенным сочетаниям (v,w) алфавита, ev,w – заранее известная среднестатистическая частота встречаемости биграммы (v,w),hv,w(i1, i2, i3,…, iL) –частота встречаемости биграммы (v,w) в тексте, расшифрованном с помощью перестановки π**, которая является итоговой для последовательности i1, i2, i3,…, iL перестановок букв алфавита, полученных в результате предварительного частотного анализа. Предложенная фитнесс-функция F показывает, насколько расшифрованный с помощью итоговой перестановки π** текст близок по своим частотным характеристикам к среднестатистическому осмысленному тексту. Чем меньше окажется значение F для конкретной перестановки π**, тем больше она будет похожа на одну из строк таблицы Виженера, и тем качественнее мы сможем расшифровать заданный шифр-текст. Поскольку генетический алгоритм не всегда находит точное решение, полученный расшифрованный текст может отличаться от исходного текста. Однако отличия будут, скорее всего, незначительные (см. рис. 2), и процесс расшифровки удастся довести до конца в «ручном режиме».
Результаты работы генетического алгоритма
Описанный выше генетический алгоритм был реализован в виде программного продукта. Для проверки его работоспособности и качества дешифрования были подготовлены тестовые задания. В некоторых тестах исходные тексты были написаны на искусственных языках с алфавитами небольшой мощности и специально подобранными неравномерными частотными профилями, т.е. частотами встречаемости букв и двухбуквенных слогов. Также в качестве исходных текстов были выбраны фрагменты литературных произведений на русском языке.
В процессе тестирования исследовалась зависимость времени и качества работы алгоритма от свойств языка (мощности алфавита, частотного профиля), параметров схемы шифрования (длины ключевого слова и исходного текста) и характеристик генетического алгоритма (размер популяции, доля скрещиваемых особей). Во всех случаях применялся одноточечный оператор скрещивания со случайным выбором точки разбиения хромосом, мутация (перестановка двух произвольных генов) происходила с вероятностью 0,05. Хотя теоретический минимум фитнесс-функции, вычисляемой по формуле (1), равен нулю, однако решение о завершении работы алгоритма принималось, если лидер популяции не менялся в течение нескольких поколений. Это объясняется тем, что указанная фитнесс-функция не обращается в нуль даже при правильно расшифрованном тексте, поскольку его частотные характеристики, скорее всего, будут отличаться от среднестатистических значений. Например, в одном из тестов с использованием семибуквенного ключевого слова был зашифрован текст длиной 650 символов на искусственном языке с десятибуквенным алфавитом. Лидер первого поколения имел значение фитнесс-функции, равное 5,9456, а абсолютный лидер (итоговая перестановка), с помощью которого шифр-текст был в итоге правильно расшифрован, имел значение фитнесс-функции, равное 1,00022, и не менялся в течение десяти поколений, хотя был обнаружен генетическим алгоритмом в восемнадцатом поколении.
В одном из тестов был зашифрован отрывок из романа А. С. Пушкина «Евгений Онегин». Длина текста составляла примерно 23000 символов, а длина ключевого слова – 14 символов. Частотный анализ позволил найти длину ключевого слова. Однако генетический алгоритм ошибся, неправильно определив одну букву в ключевом слове и пять позиций в итоговой перестановке. Текст был расшифрован неправильно, но содержал много коротких осмысленных фраз («ПОЭЗИИ ЖИВОЙ И ЯСНОЙ», «И СЕРДЦА ГОРЕСТНЫХ ЗАМЕТ»), а также узнаваемые фразы («СВЬТОЙ ИСПОЛНЕНЯОЙ ЮЕЧТЫ»). Поэтому окончательно расшифровку удалось завершить в «ручном режиме», изменив итоговую перестановку.
Генетический алгоритм показал хорошие результаты на достаточно длинных текстах. При длине текста, превышающей длину ключевого слова более чем в 2000 раз, расшифрование с помощью абсолютного лидера почти всегда выполняется правильно. Время работы алгоритма пропорционально численности популяции и доле особей, участвующих в скрещивании. Однако, как показывают результаты тестирования, расшифрование приемлемого качества достигается уже при 10 особях, половина из которых участвует в скрещивании. Бóльшая численность популяции лишь увеличивает время работы алгоритма, но почти не улучшает качество найденного решения. Например, расшифрование осмысленного текста на русском языке длиной 10000 символов при 10 особях занимает в среднем 20 сек.
Заключение
Итоги тестирования предложенного генетического алгоритма оказались вполне предсказуемыми. Во-первых, подтвердилась принципиальная возможность использовать генетический алгоритм для решения задачи криптоанализа. Для этого достаточно было превратить задачу расшифрования в задачу комбинаторной оптимизации. В качестве оптимизируемого функционала здесь выступала степень совпадения частотных профилей расшифрованного и осмысленного среднестатистического текста. При этом необходимым условием успешной работы генетического алгоритма являлось требование осмысленности к исходному тексту. Следовательно, данный алгоритм можно легко адаптировать к расшифрованию текстов не только на русском, но и на любом другом естественном языке. Для этого достаточно лишь внести соответствующие изменения в фитнесс-функцию (1).
Во-вторых, как известно, генетический алгоритм не гарантирует нахождение точного решения, даже если была правильно определена длина ключевого слова. Однако для рассматриваемой задачи это оказалось не так критично, поскольку расшифрованный текст содержал множество угадываемых слов в тех ситуациях, когда итоговая перестановка незначительно отличалась от первой строки таблицы Виженера, а именно, если число позиций, в которых они различались, не превосходило пяти. В этом случае удавалось довести процесс расшифрования до конца, но уже в «ручном режиме». Благодаря использованию генетического алгоритма основная часть работы выполнялась автоматически, а доля «ручного» труда криптоаналитика оказывалась незначительной.
В-третьих, вмешательство человека в процесс расшифровки можно сделать ещё меньшим, если повысить точность вычисления длины ключевого слова, подаваемой на вход генетическому алгоритму. Для этих целей можно использовать тест Ф. Казиски или индекс совпадения У. Фридмана. Однако здесь могут возникнуть проблемы, которые будет сложно обойти. Для естественных языков это случается, например, когда соотношение между длинами шифр-текста и ключевого слова недостаточно велико. Для расшифрования в автоматическом режиме с помощью предложенного генетического алгоритма это соотношение должно быть не менее 2000. При меньших значениях может потребоваться вмешательство человека. Это же относится и к искусственным языкам. Однако дополнительная сложность здесь возникает тогда, когда частотный профиль среднестатистического текста, написанного на данном искусственном языке, близок к равномерному. В этом случае многие биграммы встречаются в тексте с близкой частотой, а это приводит к тому, что высокую приспособленность имеют даже те особи, которые на самом деле далеки от правильного решения.
Наконец, дальнейшее совершенствование предложенного генетического алгоритма может быть связано с его распараллеливанием и распределенными вычислениями. Как известно, основные операторы и этапы генетического алгоритма – генерация начальной популяции, отбор, скрещивание, мутация, формирование нового поколения – допускают независимое выполнение. Благодаря распараллеливанию можно не только ускорить работу алгоритма, но и повысить качество расшифрования [3].
Рецензенты:
Русаков С.В., д.ф.-м.н., профессор, профессор кафедры прикладной математики и информатики, Пермский государственный национальный исследовательский университет, г. Пермь.
Тюрин С.Ф., д.т.н., профессор, профессор кафедры математического обеспечения вычислительных систем, Пермский государственный национальный исследовательский университет, г. Пермь.



