Введение
Наука и технологии последних десятилетий в разных своих областях и направлениях призваны решать многие задачи, связанные с попытками воспроизведения по внешним данным некоторых, чаще всего скрытых от прямого наблюдения объектов или различных включений в объекты как плоского (2D), так и пространственного (3D) вида. Области знания, где такие задачи ставятся и решаются в той или иной мере и с той или иной точностью и определенностью, поистине неисчерпаемы простым списком: рентгенография (медицинская и техническая), в частности, томография различной природы (ПЭТ, КТ, МРТ) – здесь само слово «томография» означает буквально «рисование слоев», дефектоскопия, звуковое, ультразвуковое и радиочастотное детектирование и зондирование, 2D и 3D моделирование реальных объектов и реконструирование археологических систем т.д. [2, 3, 4].
Значительная часть геофизических методов разведки строится на попытках моделирования внутренней структуры по внешним данным или же строится на основе анализа точечных данных – образцов, добываемых из подземных массивов. Отметим также, что различные неразрушающие методы интравидения являются одной из основных опор современной доказательной медицины, неразрушающие способы просвечивания объектов используются как средство контроля за пассажиро- и грузопотоком в ответ на вызовы распространяющегося терроризма и т.п.
В данной работе мы ставим задачи реконструкции определенного вида (не встречавшийся нам ранее в литературе), описываем класс методов, позволяющих получить решения и категоризируем их. В целях большей иллюстративности материала приводятся различные примеры, позволяющие строить определенные достаточно общие выводы. Помимо этого, в статье даются соображения, позволяющие экстраполировать методы решения задач на некоторые новые области, что позволяет считать, в определенной мере, работу в достаточной мере теоретической и имеющей широкий спектр практических приложений.
Постановки задач и обозначения
Ниже условимся считать, что в форме, напоминающей матричную, но не являющейся тем не менее таким обычным объектом как матрица, мы будем описывать некоторую 2D-область прямоугольной формы. Таким образом, мы имеем область ![]() , которую в дальнейшем будем описывать набором точек
, которую в дальнейшем будем описывать набором точек ![]() , полагая, что они являются некоторыми равномерно (что необязательно) распределенными узлами сетки
, полагая, что они являются некоторыми равномерно (что необязательно) распределенными узлами сетки ![]() в области
в области ![]() . Эту область мы может представить в такой форме:
. Эту область мы может представить в такой форме:
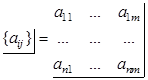 . (1)
. (1)
Здесь ![]() – индексы точек или элементов матричной формы таблицы (1), вертикальная черта справа и горизонтальная черта снизу станут понятны в дальнейшем.
– индексы точек или элементов матричной формы таблицы (1), вертикальная черта справа и горизонтальная черта снизу станут понятны в дальнейшем.
Сначала рассмотрим задачу в наиболее общем виде. Пусть элементами плоской области (1) являются некоторые (материальные) точки, обладающие той или иной проницаемостью ![]() . (2)
. (2)
Тогда, при условиях, что мы может измерить суммарный результат проникновения той или иной формы энергии через сплошную область ![]() , постулируя при этом, что в точках
, постулируя при этом, что в точках ![]() нам известны интегральные характеристики проницаемости по горизонтали или вертикали окружающего точки элементарного малого прямоугольника, сопрягающегося сторонами с соседними элементарными прямоугольниками области (за исключением граничных точек, имеющих контакт с полностью проницаемой средой; хотя было бы нетрудно постулировать, скажем, ее (среды) равномерную и отличную от области проницаемость, а затем ввести расстояния от источника энергии до границ области; впрочем, это можно сделать и иным способом (см. задачу 2), мы можем ввести такое изображение:
нам известны интегральные характеристики проницаемости по горизонтали или вертикали окружающего точки элементарного малого прямоугольника, сопрягающегося сторонами с соседними элементарными прямоугольниками области (за исключением граничных точек, имеющих контакт с полностью проницаемой средой; хотя было бы нетрудно постулировать, скажем, ее (среды) равномерную и отличную от области проницаемость, а затем ввести расстояния от источника энергии до границ области; впрочем, это можно сделать и иным способом (см. задачу 2), мы можем ввести такое изображение:
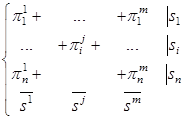 , (3)
, (3)
где вместо сплошной отделяющей справа и снизу линии (как в (1)), нам удалось имеющимися средствами редактора формул проставить только отчеркивающие отрезки. «Внутри» области теперь стоят проницаемости соответствующих прямоугольников, а справа – суммарные величины показателей (см. замечание 2) остаточной энергии ![]() после прохождения первой, второй,
после прохождения первой, второй, ![]() ой и, наконец,
ой и, наконец, ![]() ой строки. Нижний ряд (точнее, строка) под величинами проницаемости аналогичен правому ряду (столбцу), но в нем указываются остаточные значения энергии после прохождения всего соответствующего столбца наших проницаемостей теперь по вертикали.
ой строки. Нижний ряд (точнее, строка) под величинами проницаемости аналогичен правому ряду (столбцу), но в нем указываются остаточные значения энергии после прохождения всего соответствующего столбца наших проницаемостей теперь по вертикали.
Задача 1. Исходя из известных результатов наборов проницаемостей ![]() и
и ![]() , как это показано в модели (3), определить проницаемости
, как это показано в модели (3), определить проницаемости ![]() элементов области
элементов области ![]() и восстановить сплошную область
и восстановить сплошную область ![]() с требуемой точностью.
с требуемой точностью.
Решение задачи 1
Замечание 1. Ясно, что задача в общем случае не является разрешимой в силу своей недоопределенности. В самом деле, общее количество неизвестных равно ![]() , а число уравнений лишь
, а число уравнений лишь ![]() , но даже для случая
, но даже для случая ![]() задача может оказаться формально неразрешимой даже для 2 значений проницаемости, что следует из нижеприводимого примера 1.
задача может оказаться формально неразрешимой даже для 2 значений проницаемости, что следует из нижеприводимого примера 1.
Замечание 2. Для иноязычного читателя может возникнуть естественный вопрос о смысле слова «проницаемость», ибо когнитивно оно должно означать способность области быть проникнутой тем или иным видом энергии. То есть, полагая, что проницаемость некоторой подобласти равна единице, естественно предположить, что вся энергия просто проходит через такую подобласть без изменений. Но на практике, чем выше показатель проницаемости, тем хуже через такую подобласть проходит (волновая) энергия. Поэтому далее, при описании моделей примеров, мы будем исходить из обратного смысла результатов справа и снизу в модели (3): мы будем полагать, что параметра «нашей» проницаемости показывают потери энергии и, в результате справа по каждой строке или снизу по каждому столбцу, мы получаем определенные суммарные потери (тогда становится оправданным знак «+» в таблице модели).
Пример 1. Учитывая положения вышеприведенного замечания 2, запишем несколько моделей для случая ![]() , полагая, что единица отвечает некоторой сплошной (или непроводящей) среде, а нуль – пустоте:
, полагая, что единица отвечает некоторой сплошной (или непроводящей) среде, а нуль – пустоте:
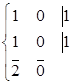 , (4а)
, (4а)
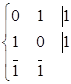 , (4b)
, (4b)
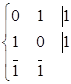 , (4c)
, (4c)
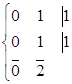 . (4d)
. (4d)
Очевидно, что даже для этого самого простого случая возникает неопределенность, если элементы размещены «равномерно». Для вариантов (4b) и (4с), таким образом, реконструкция невозможна, точнее возможна в определенной мере, но амбивалентна, т.е. не определяется однозначно. То есть «наружной информации» просто недостаточно.
Пример 2. Если рассмотреть случай квадратной области квадратной области ![]() , то с очевидностью так же будут вести себя таблицы, в которых имеется распределение нулей и единиц по «шахматной доске»: в правом и нижнем рядах суммы будут равны
, то с очевидностью так же будут вести себя таблицы, в которых имеется распределение нулей и единиц по «шахматной доске»: в правом и нижнем рядах суммы будут равны ![]() (здесь квадратные скобки означают целую часть числа). Реконструкция исходного набора, в принципе, возможна, но снова амбивалентна.
(здесь квадратные скобки означают целую часть числа). Реконструкция исходного набора, в принципе, возможна, но снова амбивалентна.
Учитывая вышеизложенное, введем некоторые очевидные ограничения на 1) проницаемости, 2) распределения и ограничимся вначале отдельными случаями. Но сперва введем понятие области дефекта ![]() : это подобласть в
: это подобласть в ![]() , в которой наблюдается дефект плотности или проницаемости (контрастируемое уменьшение или возрастание).
, в которой наблюдается дефект плотности или проницаемости (контрастируемое уменьшение или возрастание).
Задача 2 и ее решение
Поставим следующую задачу:
Задача 2. Пусть известно, что область дефекта ![]() является 1) выпуклой (и, следовательно, односвязной). 2) Пусть, для определенности,
является 1) выпуклой (и, следовательно, односвязной). 2) Пусть, для определенности, ![]() в
в ![]() вне дефекта и
вне дефекта и ![]() в дефекте. Тогда возможен следующий способ решения задачи реконструкции области
в дефекте. Тогда возможен следующий способ решения задачи реконструкции области ![]() с выпуклым дефектом
с выпуклым дефектом ![]() , названный нами «Алгоритм 1».
, названный нами «Алгоритм 1».
Алгоритм 1. Выполним следующие шаги:
Шаг 1: Записываем таблицу из пока неизвестно располагающихся нулей и единиц, а правый и нижний результаты рассматриваем как столбец ![]() и строку
и строку![]() .
.
Шаг 2. Справа от правого столбца модели записываем массив из натуральных чисел от 1 до ![]() .
.
Шаг 3. Ниже нижней строки модели записываем строку натуральных чисел от 1 до ![]() .
.
Шаг 4. Проведем массивов из пары строк и пары столбцов, например, по убыванию сверху вниз справа и по убыванию слева направо внизу.
Шаг 5. Получим массивы (пар столбцов и строк) с левым столбцом ![]() и верхней строкой
и верхней строкой ![]() . Окаймляющие столбец и строки изменили свои значения.
. Окаймляющие столбец и строки изменили свои значения.
Шаг 6. Рассмотрим теперь расширенную матрицу-таблицу модели. Ясно, что после такого переформирования у нее все единицы соберутся в левый верхний угол.
Шаг 7. В правом внутреннем столбце число «следа» должно показать точное количество единиц слева в первой строке.
Шаг 8. В левом нижнем углу «следовой» строки получится сумма всех единиц первого столбца.
Шаг 9. Восстанавливаем эти значения, начиная с левого верхнего угла расширенной таблицы-матрицы модели, заполняя единицами слева клетки в количестве, отвечающем максимальному значению вверху измененного «следового» столбца и спускаясь затем вниз/вправо с чередованием направления.
Подшаг 9а. Проверяем, снизилось ли значение при перемещении по правому «следу» вниз на 1 строчку. Если оно уменьшилось, то горизонтально исчезла одна клеточка. Если нет, то клеточка остается с единицей.
Подшаг 9b. Проверяем снижение значения. Нет – оставляем столько же клеток с единицами по вертикали, а если снизилось, то меняем единицы на нули.
Шаг 10. И т.д.
Промежуточный результат. У нас получилась область ![]() (очевидно выпуклая, как и в условии на дефект; доказательство достаточно очевидно).
(очевидно выпуклая, как и в условии на дефект; доказательство достаточно очевидно).
Финальный подалгоритм: За счет обратного упорядочивания по окаймляющим клеткам (по самому правому столбцу и самой нижней строке) всей таблицы получаем требуемый результат.
Если условие a-priori выпуклости нарушается, то возникает амбивалентность. Вообще говоря, здесь присутствует влияние определенных геометрико-топологических элементов модели. Поэтому последующее изложение дополнит.
Замечание 3. Выпуклость «следов» (это векторы или наборы натуральных чисел в наших условиях) не гарантирует выпуклости области дефекта.
Доказательство. Рассмотрим область дефекта в некоторой «грушеподобной» форме или в виде сужающегося вверх овала, а затем раздвинем ее в верхней части совсем чуть-чуть в стороны, образовав внутри небольшую вертикальную пустоту. Это можно сделать так, что выпуклость вертикального следа вообще не изменится, а на выпуклости горизонтального отпечатка это скажется незаметно. Получаем, что выпуклое по контуру и не односвязное множество имеет выпуклые следы, Q.E.D.
Решение других задач
Нетрудно заметить, что на основе вышеуказанной технологии или метода можно решать задачи с определенным усложнением, например, при наличии a-priori известной строго выпуклой дефектной области с единицами (плотность внутри) и меньшей плотности 0,5 выпуклой дефектной области вокруг. Алгоритм 1 расширяется, так как при учете вероятности «двойной» плотности (по сравнению за значением 0,5) снова сгодятся операции упорядочивания (сворачивающие дефекты с «рыхлой» границей снова в «плотный» сектор левого верхнего угла, но с вероятностью появления «половинок» после определенного ухода от верхней левой точки).
Замечание 3. Полагая, что у наблюдателя имеется возможность провести энергетическое сканирование не только в двух ортогональных направлениях, как в модели (1), но и воспользоваться диагональными сканами перпендикулярно на прямой счетчик (с учетом проницаемости окружающей среды), можно значительно уменьшить пессимизм неразрешимости Задачи 1. В Примере 1 (см. (4b), (4c) достаточно добавить диагональный след (0 или 2), и задача становится разрешимой.
Замечание 4. При инвертировании условия Задачи 2 в отношении плотностей/ проницаемостей получаем задачу, сопряженную через обратное упорядочивание (многое зависит от примерной величины пустотелого дефекта в таком случае).
Замечание 5. Случаи 3D-областей могут сводиться к послойному решению задач 2D или же применению аппарата так называемых «кубиц» (были введены автором ранее 1995 года).
О приложениях
В качестве приложений описываемых подходов могут выступать также и задачи сжатия графической (ч/б) информации по выпуклым областям. Достаточно для этого передавать не все bitmap изображение, требующее минимально ![]() бит, а лишь
бит, а лишь ![]() бит (кстати, протокол передачи может тоже оказаться проще с учетом уменьшения общего веса информации, 8 бит хватит даже на 256 градаций серого).
бит (кстати, протокол передачи может тоже оказаться проще с учетом уменьшения общего веса информации, 8 бит хватит даже на 256 градаций серого).
Другие области приложений включают в себя дефектоскопию, рентгеновскую реконструкцию, а также комбинированные методы рентгенолучевой и эхо-локационной реконструкции. Отдельный интерес представляет реконструкция по геофизическим данным, но ограниченность места не позволяет рассмотреть здесь все варианты.
Рецензенты:
Латыпов Р.Х., д.т.н., профессор, директор Института вычислительной математики и информационных технологий, КФУ, г. Казань.
Фазылов В.Р., д.ф.-м.н., профессор, кафедра анализа данных и исследования операций, КФУ, г. Казань.



