Введение
Модель синхронного генератора с демпферными контурами описывается системой из шести дифференциальных уравнений. Два первых дифференциальных уравнения записываются для поперечной и продольной обмоток статора. Три следующих уравнения записываются для обмоток ротора. В обмотки ротора входят поперечная и продольная демпферные обмотки и обмотка возбуждения. Шестое дифференциальное уравнение является нелинейным. Это уравнение описывает связь инерционного, электромагнитного и механического моментов, действующих на вал ротора. Решение этих уравнений является не простой задачей. Однако искусство моделирования состоит не в умении решать сложные уравнения, а в умении без потерь основных, главных свойств явления преобразовывать исходную сложную систему в более простую, руководствуясь при этом условиями, которым подвержена исследуемая система. Поэтому цель работы состоит в исследовании моделей генератора в условиях, когда исходную сложную систему можно упростить, но при этом не потерять основные характерные особенности модели.
Модель синхронного генератора при удаленном возмущении
Если точка приложения возмущения находится далеко от генератора, то в уравнениях генератора допускается не учитывать электромагнитные переходные процессы в демпферных контурах, так как демпферные контуры короткозамкнуты и, следовательно, их токи имеют только свободную – апериодическую составляющую, которая быстро затухает, не успев дождаться появления возмущения. Из-за большой инерционности ротора скорость ротора изменяется медленно, поэтому можно считать, что скольжение отсутствует ![]() . И уравнения для описания переходных процессов генератора приобретают вид [4; 5]:
. И уравнения для описания переходных процессов генератора приобретают вид [4; 5]:
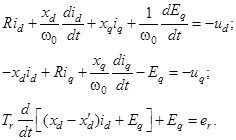 (1)
(1)
Здесь ![]() – синхронная ЭДС по поперечной оси, величина пропорциональна току возбуждения
– синхронная ЭДС по поперечной оси, величина пропорциональна току возбуждения ![]() , величина, которая подлежит определению.
, величина, которая подлежит определению. ![]() – постоянная времени контура возбуждения при замкнутых контурах цепи статора.
– постоянная времени контура возбуждения при замкнутых контурах цепи статора. ![]() - продольный и поперечный токи статора.
- продольный и поперечный токи статора. ![]() – ЭДС, пропорциональная напряжению статора.
– ЭДС, пропорциональная напряжению статора. ![]() – основные технические данные машины: синхронные реактивные сопротивления по поперечной и продольной осям, переходное сопротивление по продольной оси, активное сопротивление обмотки статора соответственно.
– основные технические данные машины: синхронные реактивные сопротивления по поперечной и продольной осям, переходное сопротивление по продольной оси, активное сопротивление обмотки статора соответственно.
При решении дифференциальных уравнений (1) удобней использовать непрерывно изменяющуюся величину ![]() – переходная ЭДС по поперечной оси, пропорциональная потокосцеплению
– переходная ЭДС по поперечной оси, пропорциональная потокосцеплению ![]() контура возбуждения. А для определения изменяющейся скачком синхронной электродвижущей силы
контура возбуждения. А для определения изменяющейся скачком синхронной электродвижущей силы ![]() использовать соотношение [1; 2]:
использовать соотношение [1; 2]:
![]()
При этом также можно не учитывать переходные процессы в обмотках статора генератора, считая, что к появлению возмущения в обмотках статора возник установившийся режим. На роторе генератора остается только один контур – обмотка возбуждения, ориентированная по оси d (продольная ось ротора), и уравнения принимают вид:
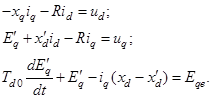 (2)
(2)
Таким образом, система алгебраических и дифференциальных уравнений при принятом допущении описывает переходные процессы в явнополюсном синхронном генераторе без демпферных контуров. Алгебраические уравнения установившегося режима получаются из системы (2), если приравнять производные уравнения нулю d / dt = 0.
Решение разбивается на 3 этапа
1. Определяем зависимость токов статора ![]() от напряжений статора
от напряжений статора ![]() и переходной ЭДС
и переходной ЭДС ![]()
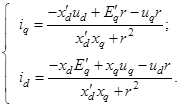 (3)
(3)
2. Далее находим значения ЭДС ![]() в установившемся режиме, подставив вместо тока
в установившемся режиме, подставив вместо тока ![]() его выражение (4)
его выражение (4)
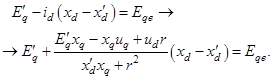
В результате получаем:
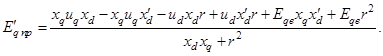
Решаем дифференциальное уравнение для определения переходной ЭДС ![]() при известных напряжения статора. Предварительно приводим уравнение к нормальной форме
при известных напряжения статора. Предварительно приводим уравнение к нормальной форме
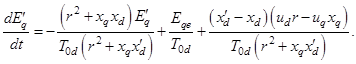
Из последнего уравнения следует, что постоянной времени переходного процесса является величина, равная выражению
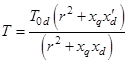 .
.
Это выражение, при пренебрежении сопротивления статорной обмотки, преобразуется в известное соотношение
![]()
Разберем несколько примеров расчета переходных процессов с рассмотренной моделью генератора.
Приведем расчет для генератора со следующими паспортными данными: ![]() =1,1;
=1,1; ![]() =0,6;
=0,6; ![]() = 0,3;
= 0,3; ![]() = 1,0;
= 1,0; ![]() = 0,004;
= 0,004; ![]() = 5с.;
= 5с.; ![]() = 1.
= 1.
Пример. Проведем моделирование для нагруженного генератора, в котором происходит трехфазное короткое замыкание с длительностью 0,8 с.
а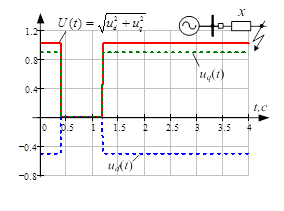 б
б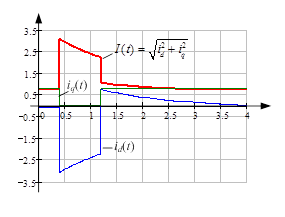 в
в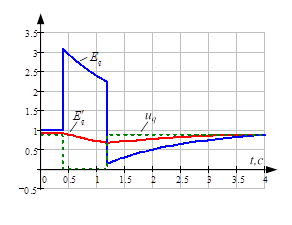
Рис. 1. Результаты расчётов: а – продольное и поперечное напряжение генератора, амплитуда напряжения; б – токи статора; в – поперечное напряжение генератора, переходная ЭДС и ЭДС генератора, пропорциональная току возбуждения
Прокомментируем полученные зависимости. При коротком замыкании напряжение генератора резко спадает до нуля (рис. 1а), при этом мгновенно возрастают токи статора (рис. 1б). При возрастании токов статора увеличивается потокосцепление якоря, что в свою очередь мгновенно вызовет реакцию обмоток возбуждения. Эта реакция сопровождается мгновенным увеличением тока возбуждения (синяя линия на рис. 1в. Синхронная ЭДС, пропорциональная току возбуждения ![]() ). Увеличение тока возбуждения не увеличивает потокосцепление обмотки возбуждения. Потокосцепление обмотки возбуждения не может изменяться скачком, поэтому переходная ЭДС
). Увеличение тока возбуждения не увеличивает потокосцепление обмотки возбуждения. Потокосцепление обмотки возбуждения не может изменяться скачком, поэтому переходная ЭДС ![]() , пропорциональная потокосцеплению контура возбуждения, изменяется непрерывно-плавно, уменьшаясь до окончания короткого замыкания (красная линия на рис. 1в). После окончания короткого замыкания синхронная и переходная ЭДС апериодически стремятся к своему установившемуся значению.
, пропорциональная потокосцеплению контура возбуждения, изменяется непрерывно-плавно, уменьшаясь до окончания короткого замыкания (красная линия на рис. 1в). После окончания короткого замыкания синхронная и переходная ЭДС апериодически стремятся к своему установившемуся значению.
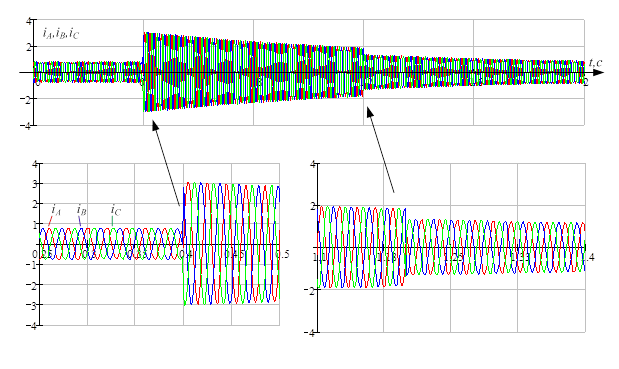
Рис. 2. Токи статора в системе координат статора
Пример. Приведем пример с автоматическим повторным включением. Произошло короткое замыкание, и в момент времени 0,4 с короткое замыкание отключается. Далее через 0,8 с произошло повторное включение короткого замыкания. Пример демонстрирует, что после повторного включения может оказаться, что условия повторного короткого замыкания тяжелее первоначальных, то есть ток при повторном замыкании достигает большей величины.
а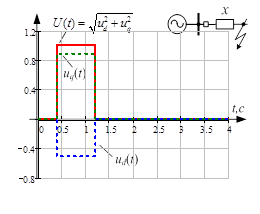 б
б
Рис. 3. Результаты расчётов: а – продольное и поперечное напряжение генератора, амплитуда напряжения; б – токи статора
а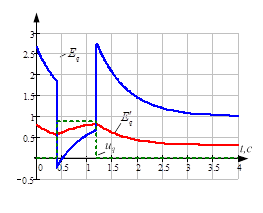 б
б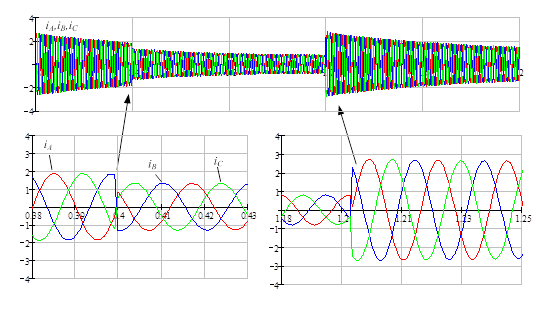
Рис. 4. Результаты расчётов: а – поперечное напряжение генератора, синхронная ЭДС и ЭДС генератора, пропорциональная току возбуждения; б – токи статора в системе координат статора. Ток после повторного включения больше первоначального
Модель синхронного генератора при близком возмущении
Рассмотрим модель синхронного генератора, считая, что точка приложения возмущения находится близко к генератору. В этом случае следует учитывать переходные процессы в обмотках статора и, следовательно, к предыдущим уравнениям добавляются слагаемые, содержащие информацию о переходных процессах в цепях статора. Как и прежде, из-за большой инерционности ротора скорость ротора изменяется медленно, поэтому можно считать, что скольжение отсутствует ![]() , и тогда можно записать [4]:
, и тогда можно записать [4]:
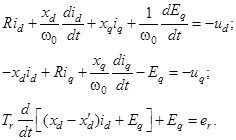 (4)
(4)
Приведем пример использования приведенных уравнений для генератора со следующими паспортными данными: ![]() =0,65;
=0,65; ![]() = 1,0;
= 1,0; ![]() = 0,004;
= 0,004; ![]() = 5 с;
= 5 с; ![]() = 1.
= 1.
Систему уравнений (4) будем решать, считая, что режим, предшествующий короткому замыканию, являлся режимом холостого хода, в котором токи статора ![]() и
и ![]() равнялись нулю. Следовательно, начальными данными к решению уравнений будут величины
равнялись нулю. Следовательно, начальными данными к решению уравнений будут величины ![]() , а напряжения в уравнениях превращаются в нуль
, а напряжения в уравнениях превращаются в нуль ![]() , так как на выходе генератора короткое замыкание. Поскольку в этом режиме ЭДС возбуждения величина постоянная, то последнее из уравнений (4) дает для нее следующее начальное значение
, так как на выходе генератора короткое замыкание. Поскольку в этом режиме ЭДС возбуждения величина постоянная, то последнее из уравнений (4) дает для нее следующее начальное значение ![]() [2].
[2].
Первый этап – определение принужденных составляющих. В дифференциальных уравнениях следует положить все производные нулю. Так как в установившемся режиме величины не изменяются – они постоянны, а производные постоянных величин раны нулю. Таким образом, система дифференциальных уравнений преобразуется в систему алгебраических уравнений. Решение этой системы приведем ниже. Решения получены с помощью программно-интегрированной среды MathCAD с использованием функций Given и Find [3]:
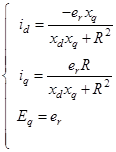
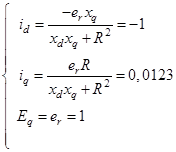 (5)
(5)
Второй этап – это решения дифференциальных уравнений методом пространства состояний.
Метод пространства состояний распространяется на системы любого порядка, важное его преимущество – это наличие матрицы состояния и вектора правых частей, с помощью которых легко определить собственные числа и определить корни характеристического уравнения, а также если записать А-1·В, где А – матрица состояний, В – вектор правых частей, то можно рассчитать установившийся режим.
Следует добавить, что нелинейные модели второго порядка позволяют выявлять многие принципиальные особенности поведения динамических систем. Также данный метод позволяет унифицировать описание одномерных и многомерных систем, может применяться к нелинейным и нестационарным системам, и с помощью него удобно решать задачи на ЭВМ.
Приводим уравнения (5) к нормальной форме, разрешая их относительно производных [3].
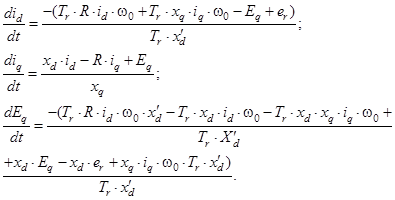
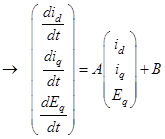 (6)
(6)
Матрица состояний и вектор правых частей имеют вид:
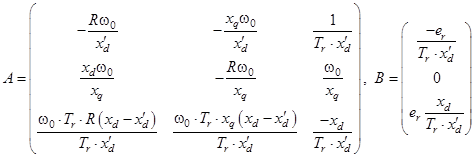
Собственные числа матрицы состояний дают нам корни характеристического уравнения. С помощью программы MathCAD, используя функцию eigenvals(A), определяем собственные числа:
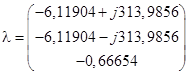
Полученные корни говорят о том, что в решении будут присутствовать медленная апериодическая и быстро затухающая колебательная составляющие, а с учетом принужденных составляющих (5) и постоянная составляющая.
Третий этап – Решение системы дифференциальных уравнений. Построение графических зависимостей и интерпретация результатов.
Для решения системы (6) используем программу MathCAD с использованием функции rkfixed() – метод Рунге - Кутта 4 порядка.
С помощью обратного преобразования Парка - Горева получаем фазные токи статора [3; 4; 6] ![]()
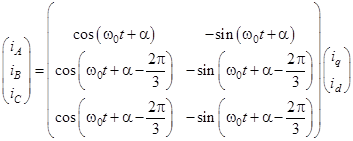 .
.
Здесь ![]() – угол между положением продольной оси ротора генератора и осью фазы А.
– угол между положением продольной оси ротора генератора и осью фазы А.
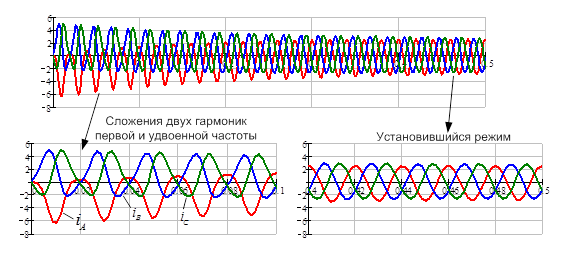
Рис. 5. На начальном этапе видно характерное проявление сложения двух гармоник. Составляющая второй гармоники быстро затухает, и остается составляющая первой гармоники.
Полученные графики показывают, что на начальном этапе короткого замыкания в токах статора возникает гармоника удвоенной частоты, что свидетельствует о несимметрии ротора. Магнитный поток от апериодической слагающей токов трех фаз статора практически неподвижен в пространстве. В обмотке возбуждения он наводит ЭДС синхронной частоты, которая создает в этой обмотке переменный ток той же частоты. В результате возникает пульсирующий магнитный поток, неподвижный относительно ротора. Пульсирующий поток можно разложить на два потока, вращающихся в противоположную сторону, один из которых неподвижен относительно статора, а другой вращается относительно статора с удвоенной частотой.
Выводы
Модели синхронных генераторов, предложенные в работе, позволяют сделать следующие заключения.
Если место приложения возмущающего воздействия находится в удаленной точке от синхронного генератора, то можно не учитывать быстрые переходные процессы, происходящие в демпферных контурах и контурах статора.
Расчеты переходных процессов синхронного генератора по предложенной модели показывают, что после повторного включения может оказаться, что условия повторного короткого замыкания тяжелее первоначальных условий, то есть ток при повторном замыкании достигает большей величины.
Если место приложения возмущающего воздействия находится в точке, близкой к синхронному генератору, тогда при расчете режимов в моделях генератора следует учитывать переходные процессы в обмотках статора.
Предложенная модель хорошо согласуется с известным фактом, что на начальном этапе переходного процесса токи статора имеют гармоники удвоенной частоты.
Применение моделей возможно в сетях, содержащих синхронные генераторы, и для проектирования объектов, содержащих генераторы.
Рецензенты:
Усов Ю.П., д.т.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.
Сивков А.А., д.т.н., профессор кафедры ЭПП ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.



