Введение. Работа любого промышленного объекта заключается не только в реализации соответствующих технологических процессов и выпуске продукции, но и сопровождается той или иной формой и степенью техногенного влияния на окружающую среду. В современных условиях техногенное влияние крупного промышленного объекта может быть довольно существенным и проявляться в загрязнениях воздуха, воды вредными веществами, газами и т.п.
Очень важно своевременно получать и обрабатывать информацию о техногенных характеристиках технологических процессов [1]. Такая информация позволит внести необходимые поправки в производственный процесс и нормализовать экологическую обстановку.
Крупное промышленное предприятие обычно характеризуется довольно большим объемом информации о техногенных и производственных процессах. Поэтому рациональное представление соответствующей информации с точки зрения удобства ее восприятия, обработки и дальнейшего использования имеет большое значение. В этом отношении достаточно обоснованными и перспективными будут матричные модели [2–4] представления информации. Представление информации в виде матрицы не только компактно, удобно визуально, но и предпочтительно с точки зрения дальнейшей обработки информации.
Материалы и методы. Матрицу как цельный математический образ можно применять для обработки информации, эффективно используя матричную алгебру. Кроме того, действия над матрицами легко реализуются на компьютере, что особенно важно для анализа информации в режиме on-line и ее использовании в общей информационно-измерительной системе.
Матричную модель представления и анализа функции можно построить следующим образом. Сначала формируется матрица текущих параметров техногенного цикла. Предположим, что строки матрицы относятся к какому-то подразделению промышленного предприятия, например, конкретно к какому-либо цеху. Обозначим цеха номерами 1, 2, 3,…, n. Предположим далее, что каждый цех (например, первый) характеризуется какими-то вредными проявлениями, выражаемыми количественно параметрами а11, а12…а1m. Эти параметры располагаются в строке, соответствующей номеру цеха. Образование следующей строки матрицы, относящейся ко второму цеху, выполняется аналогичным образом.
Число строк матрицы равно числу составляющих промышленное предприятие (объект) подразделений, в данном случае – числу анализируемых цехов. Число столбцов матрицы равно максимальному числу учитываемых техногенных факторов. Причем параметры однотипных техногенных факторов каждого цеха записываются друг под другом в одном столбце; разнотипные факторы – в разные столбцы. Если в цеху отсутствует какой-либо из учитываемых в других цехах фактор, то этот элемент матрицы записывается как «0». Окончательно матрица примет вид:
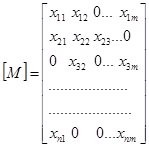 (1)
(1)
где: xk,i – переменный параметр, относящийся к k-му цеху и характеризующий проявление i-го техногенного фактора.
Нули вместо некоторых элементов матрицы [М] проставлены произвольно, для иллюстрации, их физическая интерпретация пояснялась раньше. Каждое предприятие характеризуется соответствующим техногенным циклом. Образованную матрицу [M] можно считать исходной для дальнейшей оценки техногенного цикла и для дальнейшей обработки информации.
Для оценки отклонений реальных параметров техногенного цикла от допустимых формируется матрица допустимых значений [N]. Структурно матрица [N] повторяет матрицу [М]; различие состоит в том, что элементами матрицы [N] являются допустимые значения контролируемых параметров:
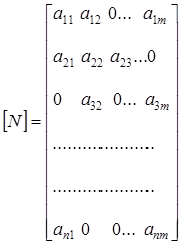 (2)
(2)
где: aki – допустимый параметр, относящийся к k-му цеху и характеризующий проявление i-го техногенного фактора.
Дальнейший анализ информации заключается в получении матрицы абсолютных ![]() и относительных
и относительных ![]() отклонений. Матрица абсолютных отклонений
отклонений. Матрица абсолютных отклонений ![]() получается как разность матрицы [M] и [N]:
получается как разность матрицы [M] и [N]:
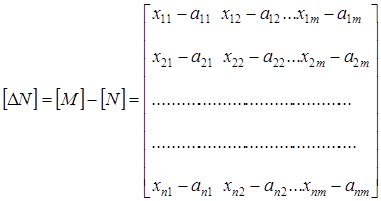 (3)
(3)
Матрица относительных отклонений ![]() получается из матрицы
получается из матрицы ![]() преобразованием ее элементов к нормальному виду, т.е. к выражению отклонений в %:
преобразованием ее элементов к нормальному виду, т.е. к выражению отклонений в %:
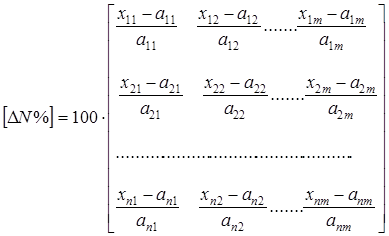 (4)
(4)
Для определения цеха с наиболее опасным техногенным влиянием предлагается ввести интегральный показатель превышения реальных значений по отношению к допустимым параметрам техногенного цикла. При его вычислении необходимо учитывать только превышения соответствующих параметров по сравнению с их допустимым значением и не учитывать значения, меньшие допустимой величины, т.е. не учитывать отрицательные элементы матрицы ![]() . Значения параметров, меньших допустимой нормы, не должны учитываться в интегральном показателе потому, что, с одной стороны, соответствующие факторы не оказывают негативного влияния на окружающую обстановку и, с другой стороны, искажают значения интегрального показателя и адекватность его толкования.
. Значения параметров, меньших допустимой нормы, не должны учитываться в интегральном показателе потому, что, с одной стороны, соответствующие факторы не оказывают негативного влияния на окружающую обстановку и, с другой стороны, искажают значения интегрального показателя и адекватность его толкования.
Для выполнения этого условия матрица ![]() преобразуется в матрицу
преобразуется в матрицу ![]() . Соответствующие операции должны быть заложены в программу вычисления интегральных параметров. Полученная после преобразования матрица умножается на единичную матрицу – столбец, число строк в которой равно числу строк в матрице
. Соответствующие операции должны быть заложены в программу вычисления интегральных параметров. Полученная после преобразования матрица умножается на единичную матрицу – столбец, число строк в которой равно числу строк в матрице ![]() :
:
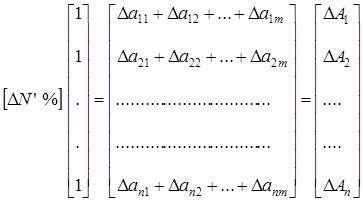 (5)
(5)
где: ![]() – относительное превышение по отношению к допустимому параметру, относящегося к k-му цеху и характеризующего проявление i-го техногенного фактора;
– относительное превышение по отношению к допустимому параметру, относящегося к k-му цеху и характеризующего проявление i-го техногенного фактора;
![]() – интегральный показатель вредного техногенного влияния k-го цеха.
– интегральный показатель вредного техногенного влияния k-го цеха.
Имея суммарную информацию по отдельным конкретным цехам, можно направить главные усилия на нормализацию положения именно туда, где положение является наихудшим.
Если техногенный вред, наносимый нарушениями допустимых показателей, существенно отличается по отдельным факторам матрицы, то для адекватной оценки техногенной ситуации в матрицу ![]() следует ввести весовые коэффициенты.
следует ввести весовые коэффициенты.
Методика определения весовых коэффициентов ![]() заключается в следующем. Суммарное влияние (суммарный вредный эффект) от превышения допустимого показателя на 1 % каждого из техногенных факторов, сопутствующих технологическим процессам данного объекта (промышленного предприятия) независимо от того, проявляется ли влияние данного фактора в рассматриваемый период времени или нет, условно принимается за «1», т.е.:
заключается в следующем. Суммарное влияние (суммарный вредный эффект) от превышения допустимого показателя на 1 % каждого из техногенных факторов, сопутствующих технологическим процессам данного объекта (промышленного предприятия) независимо от того, проявляется ли влияние данного фактора в рассматриваемый период времени или нет, условно принимается за «1», т.е.:
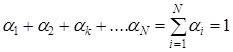 , (6)
, (6)
где: N – общее число всех разнородных техногенных факторов на промышленном предприятии (в общем случае ![]() >m).
>m).
В формуле (1) влияние каждого i-го фактора определяется на основании специальных исследований и опытных данных.
Весовые коэффициенты ![]() вводятся в матрицу
вводятся в матрицу ![]() умножением каждого k-го элемента матрицы на соответствующий весовой коэффициент. В этом случае интегральные показатели в правой части уравнения (5) будут отражать не суммарное процентное превышение всех влияющих факторов над их допустимыми значениями, а степень реального техногенного вреда (в условных единицах), который приносит тот или иной цех в рассматриваемый момент (или промежуток) времени, что является более представительной характеристикой.
умножением каждого k-го элемента матрицы на соответствующий весовой коэффициент. В этом случае интегральные показатели в правой части уравнения (5) будут отражать не суммарное процентное превышение всех влияющих факторов над их допустимыми значениями, а степень реального техногенного вреда (в условных единицах), который приносит тот или иной цех в рассматриваемый момент (или промежуток) времени, что является более представительной характеристикой.
Как уже указывалось, достоверная информация о техногенных проявлениях технологических процессов на промышленном предприятии позволит наметить и реализовать мероприятия по нормализации деятельности предприятия в отношении его техногенных проявлений.
В данной статье предложена методика матричного представления и анализа информации по техногенным факторам производственного процесса. Однако такая методика может быть использована и для анализа технологических процессов предприятия с точки зрения оценки их отклонения от требуемых параметров, непосредственно определяющих качество производимой продукции.
В общем случае может быть составлена матрица, объединяющая информацию о параметрах технологических процессов, определяющих как качество выпускаемой продукции, так и степень техногенного влияния предприятия. В этом случае матрица, характеризующая техногенные процессы предприятия, будет частью общей информационной матрицы параметров в их производственных процессах, включая техногенные циклы. Интегральные оценки отклонений от заданных технологических и техногенных нормативов в этом случае будут учитывать как вредное техногенное воздействие, так и экономический ущерб, для деятельности предприятия значительно повышая качество и надежность сложных систем.
Выводы. Предложенная авторами матричная форма представления и анализа информации может быть использована не только для анализа обработки информации и управления работой промышленного предприятия, но и для анализа состояния различных сложных экономических, социальных, природных и других систем [5–10].
Рецензенты:
Каменецкий Е.С., д.ф.-м.н., заведующий отделом математического моделирования Федеральное государственное бюджетное учреждение науки Южный математический институт ВМЦ РАН РСО-А, г. Владикавказ.
Лолаев А.Б., д.т.н., профессор, и.о. директора, Северо-Осетинский филиал ОАО «МРСК Северного Кавказа», г. Владикавказ.



