Введение
В работе моделируется связь параметров электромагнитных сигналов (ЭМС) гетерогенных слоистых и дефектных структур с детерминированным акустическим воздействием. В качестве физической модели в гетерогенных диэлектрических структурах используется возбуждение ЭМС в результате акустоэлектрических преобразований. Лабораторными экспериментальными исследованиями показано [1, 8], что такие преобразования являются одним из основных способов возбуждения ЭМС в гетерогенных материалах. Известно [4], что при подготовке разрушения твердых тел, в том числе и горных пород, наряду с имеющимися объемными дефектами, возникают протяженные нарушения в виде микротрещин. При прорастании трещин возникают акустические импульсы с параметрами, определяемыми ее размерами и скоростью раскрытия [2, 5, 7].
Методика
В расчетах использовалась модель образца со слоистой диэлектрической структурой, который разделен на четыре равные части. Две крайние части имели плотность ρ=103 кг/м3, а средние части имели плотность 2·103 кг/м3 и 3·103 кг/м3 соответственно. Возбуждение производили точечным источником, расположенным на границе диэлектрического слоистого образца. Акустические возмущения имели вид сферических волн, которые приводили в движение двойные электрические слои на границах раздела сред и локальных неоднородностях образца.
Расчеты представим в следующей последовательности. Сначала определим распределение возмущений в модели путем решения нестационарного уравнения акустики с последующим определением распределения давления, скорости и плотности среды. Затем решим задачу возбуждения ЭМС колеблющимися зарядами или двойными электрическими слоями. Рассмотрим задачу возбуждения электромагнитных волн точечными диполями в среде с неоднородной диэлектрической проницаемостью.
Расчеты возникающих смещений и давления в определенных точках модельной среды будем проводить в пренебрежении поперечных ультразвуковых волн. Распространение ультразвука в образце в одномерном приближении описывается следующими уравнениями акустики [2]:
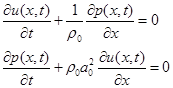 .
.
Здесь ![]() – смещение точек среды,
– смещение точек среды, ![]() – давление,
– давление, ![]() – плотность и
– плотность и ![]() – скорость распространения ультразвука в среде. Поскольку среда является слоисто-неоднородной, то распределение скорости акустической волны и плотности среды можно задать в виде кусочно-постоянных функций (рис.1).
– скорость распространения ультразвука в среде. Поскольку среда является слоисто-неоднородной, то распределение скорости акустической волны и плотности среды можно задать в виде кусочно-постоянных функций (рис.1).
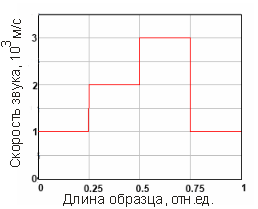
Рис. 1. Заданные значения скорости ультразвука в модельном образце со слоистой структурой
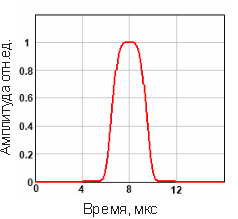
Рис. 2. Распределение давления акустического импульса на границе ввода
Экспериментальная часть
На вход образца подавали детерминированный акустический сигнал в виде импульсного воздействия заданной формы (рис. 2). Запишем уравнение в виде, удобном для численного моделирования:
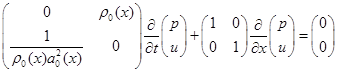 (1)
(1)
Решение уравнения (1) производили методом конечных элементов [6]. Результат решения уравнения приведен на рис. 3. Разными цветами на рис. 3, а показаны изменения скорости смещения частиц среды в разные промежутки времени при распространении акустического импульса через слоисто-неоднородный образец, а на рис. 3, б – динамика изменения давления, возникающего при таких смещениях. Границы слоистого раздела образца показаны вертикальными штриховыми линиями. Во врезке на рис. 3 в правом верхнем углу показаны моменты времени (в секундах), для которых были построены графики этих распределений.
а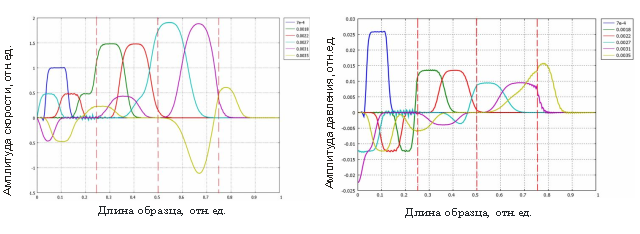 б
б
Рис. 3. Результат решения уравнения акустики: а) скорость смещения точек в слоисто-неоднородном образце; б) возникающее давление в точках
Таким образом, при прохождении акустических импульсов через среду со сложным структурным строением каждому моменту времени соответствует определенное смещение частиц и давление.
При прохождении акустического импульса через раздел сред, на границах возникают его отражения и преломление, а также колебания двойных электрических слоев. Колебания приводят к изменениям дипольных моментов и, как следствие, к излучению ЭМС. Распределение давления в фиксированной точке пространства, а именно – в точке раздела сред, будет зависеть только от времени ![]() . Результат воздействия этого возмущения на границу раздела можно описать дифференциальным уравнением:
. Результат воздействия этого возмущения на границу раздела можно описать дифференциальным уравнением:
![]() ,
,
где ![]() – пространственная координата двойного электрического слоя, соответствующая отклонению слоя от положения равновесия,
– пространственная координата двойного электрического слоя, соответствующая отклонению слоя от положения равновесия, ![]() – основная частота колебаний,
– основная частота колебаний, ![]() – коэффициент упругости,
– коэффициент упругости, ![]() – импульсное акустическое воздействие. Для решения этого уравнения использовали численный метод Рунге – Кутта 4-го порядка, предварительно записав его в виде системы уравнений первого порядка:
– импульсное акустическое воздействие. Для решения этого уравнения использовали численный метод Рунге – Кутта 4-го порядка, предварительно записав его в виде системы уравнений первого порядка:
![]()
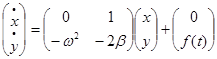 . (2)
. (2)
Полученное решение является плечом диполя с зарядом ![]() , которое смещается прямо пропорционально изменениям координаты
, которое смещается прямо пропорционально изменениям координаты ![]() . В результате дифференцирования выражения (2) получим ток, пропорциональный скорости смещения:
. В результате дифференцирования выражения (2) получим ток, пропорциональный скорости смещения:
![]() . (3)
. (3)
Это выражение пропорционально первому уравнению системы (2):
![]() . (4)
. (4)
Таким образом, определены изменения заряда ![]() и тока смещения
и тока смещения ![]() . Полученные решения
. Полученные решения ![]() и
и ![]() раскладывались в ряд Фурье:
раскладывались в ряд Фурье:
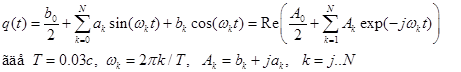 . (5)
. (5)
Коэффициенты разложения определяются выражениями:
![]()
Аналогичные операции справедливы и для тока смещения (3–5).
Поскольку решение дифференциального уравнения получено в дискретном виде, то для определения коэффициентов разложения использовалось быстрое преобразование Фурье при значениях ![]() . Результаты расчетов заряда
. Результаты расчетов заряда ![]() , тока смещения
, тока смещения ![]() и их спектров для разных импульсных функций приведены на рис. 4 и рис. 5 соответственно.
и их спектров для разных импульсных функций приведены на рис. 4 и рис. 5 соответственно.
а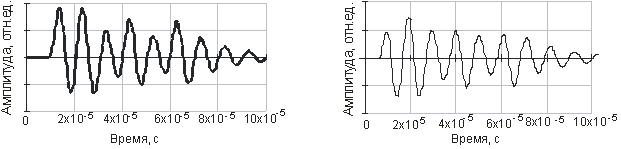 б
б
Рис. 4. Изменения на границе раздела сред: а) заряда ![]() ; б) тока смещения
; б) тока смещения ![]()
На рис. 4 видно, что изменение заряда на двойных электрических слоях под действием акустической волны приводит к возникновению и протеканию тока через образец. Рассчитанные амплитудно-частотные спектры изменяющегося заряда ![]() и тока смещения
и тока смещения ![]() приведены на рис. 5, а и 5, б соответственно. Отличие наблюдается только в низкочастотной области спектров, поскольку заряд есть низкочастотная версия тока, в спектре заряда присутствуют низкочастотные компоненты. В результате изменений заряда
приведены на рис. 5, а и 5, б соответственно. Отличие наблюдается только в низкочастотной области спектров, поскольку заряд есть низкочастотная версия тока, в спектре заряда присутствуют низкочастотные компоненты. В результате изменений заряда ![]() и тока смещения
и тока смещения ![]() слоистая диэлектрическая структура будет излучать ЭМС с параметрами, определяемыми распространяющимся детерминированным акустическим импульсом.
слоистая диэлектрическая структура будет излучать ЭМС с параметрами, определяемыми распространяющимся детерминированным акустическим импульсом.
а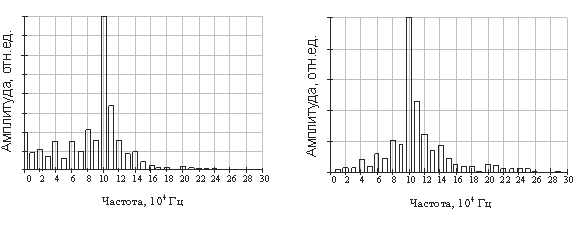 б
б
Рис. 5. Амплитудно-частотный спектр распределения: а) заряда ![]() ; б) тока смещения
; б) тока смещения ![]()
Таким образом, произведено математическое моделирование следующих процессов:
- возбуждения электромагнитных сигналов импульсным акустическим воздействием;
- влияния слоистости образцов на параметры электромагнитного отклика при детерминированном акустическом воздействии на такие структуры;
- изменение параметров ЭМС при разных амплитудах акустического воздействия на дефектную структуру с постоянным зарядом.
Результаты
Расчеты по приведенным моделям показали, что амплитудно-частотные параметры излучаемых электромагнитных сигналов находятся в непосредственной связи с характеристиками детерминированных акустических воздействий и зарядовым состоянием слоистых и дефектных структур. В реальных экспериментах акустическое возбуждение образцов диэлектрических материалов, в том числе горных пород, осуществляли с помощью пьезоэлектрического излучателя или ударом шарика из пружинного устройства. Акустическое воздействие имело форму близкую к виду возбуждения, используемого для расчетов и приведенного на рис. 2.
Рецензенты:
Канев Ф.Ю., д.ф.-м.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.
Усов Ю.П., д.т.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.



