Рассмотрим частотный метод решения задачи о продольных колебаниях стержней ступенчато-переменного сечения с учетом или без учета рассеяния энергии при соударении с жестким препятствием, который будем сравнивать с известным волновым решением [2] и решением в виде ряда по формам колебаний (14) [2].
Дифференциальное уравнение продольных колебаний стержня с учетом сил внутреннего сопротивления имеет вид [1]:
. (1)
Зададим следующие граничные и начальные условия:
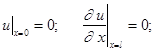
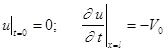. (2)
Преобразуем уравнение (1) и граничные условия (2) по Лапласу при заданных начальных условиях (2). Тогда уравнение (2) и граничные условия (2) запишутся следующим образом:
; (3)
,
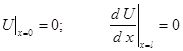где 
– преобразованные по Лапласу перемещения точек стержня; р – параметр преобразования Лапласа.
Уравнение (3) без учета рассеяния энергии (при 
= 0) примет вид:
. (4)
Для полученного неоднородного дифференциального уравнения решается краевая задача, заключающаяся в нахождении преобразованных по Лапласу краевых продольных сил, как функций краевых перемещений.
Для этого рассмотрим однородное уравнение продольных колебаний стержня с учетом рассеяния энергии
(5)
Обозначая
и переходя к новой переменной 
, получим вместо (5)
(6)
Если
, где 
– частотный параметр, то
.
Решение однородного уравнения (6) имеет вид:
,
где 
.
Постоянные интегрирования с1 и с2 находим из начальных условий:
u = u0 ; N = N0,
где 
;
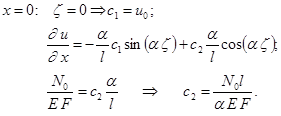
Т.е. 
;
.
Данному решению соответствует следующая матрица переноса:
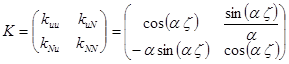. (7)
Подставив в формулы метода перемещений полученные выражения для элементов матрицы переноса, получим [5]:
;
(8)
;
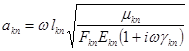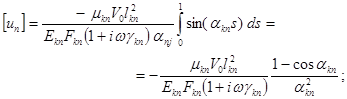
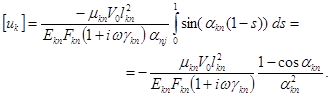
Индексы n и k указывают соответственно начало и конец участка стержня. А геометрические и физические константы с индексами nk и kn относятся к конкретному участку стержня.
Разбивая стержень на элементы, пользуясь формулами (8), составим уравнения динамического равновесия узлов. Эти уравнения представляют собой систему уравнений для неизвестных узловых перемещений. Поскольку соответствующие коэффициенты получаются точным интегрированием, длина участков стержня не ограничена.
Решая полученную систему уравнений при , строим амплитудо-фазо-частотные характеристики для интересующих нас сечений стержня. Эти АФЧХ можно рассматривать как графический образ одностороннего преобразования Фурье, который совпадает с преобразованием Лапласа при импульсных воздействиях. Поскольку все особые точки соответствующих выражений лежат левее мнимой оси, обратное преобразование можно осуществлять, полагая , т.е. используя построенные АФЧХ. Задача по построению АФЧХ, где в качестве силового воздействия фигурирует поле начальных скоростей, умноженное на плотность стержня, является вспомогательной. Обычно АФЧХ строятся от воздействия возмущающих сил, затем численным интегрированием или каким-либо иным способом осуществляется обратное преобразование Лапласа.
В качестве простого примера рассмотрим прямолинейный стержень длины l, который продольно соударяется с жестким препятствием со скоростью V0 (рис. 1).
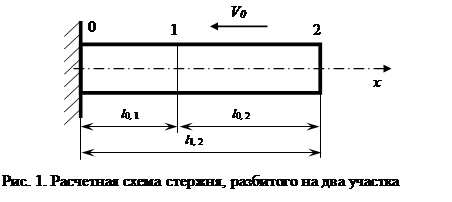
Определим смещение точек стержня после удара. Будем считать, что после удара контакт между препятствием и стержнем сохраняется, т.е. отскок стержня не происходит. Если связь является неудерживающей, то задача может рассматриваться как кусочно-линейная. Критерием перехода к другому варианту решения является смена знака скорости в точке контакта.
В монографии Лаврентьева М.А., Шабата Б.В. [2] дано волновое решение уравнения (4):
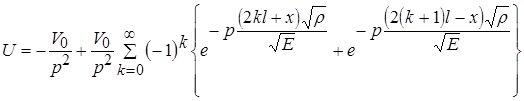
и найден его оригинал
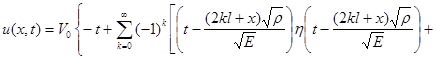
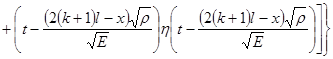, (9)
где 
– единичная ступенчатая функция.
Другой подход к решению этой задачи может быть осуществлен частотным методом, описанным в [4]. Применительно к данной задаче будем иметь:
; 
;
; 
;
; 
;
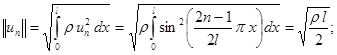
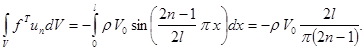
Тогдa:
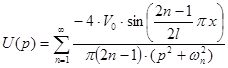. (10)
Найдем оригинал (11)
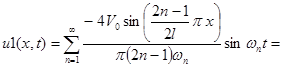
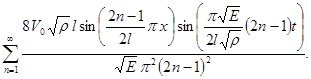
Решим эту же задачу частотным способом. Из уравнения равновесия 1-го узла:
(12)
получим формулу для перемещения конца стержня 
.
Теперь, если тестовый стержень постоянного сечения разбить на два произвольных участка длины l1и l2 (см. рис. 1), то условия равновесия узлов будут таковы:
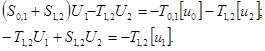(13)
В результате решения системы (13) получаем графики АФЧХ для перемещений в 1 – ом и 2 – ом сечениях (U1и U2 соответственно). Так, изображение для краевого перемещения в замкнутом виде, с учетом рассеяния энергии, в случае (12) и (13) совпадает и имеет вид:
. (14)
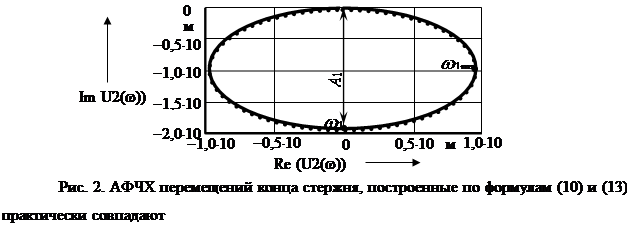
Проверим совпадение результатов на конце стержня. На рис. 2 представлены графики решения (10) при x = l0,1 и в результате решения системы (13). Они полностью совпадают.
Для получения переходного процесса может быть использовано дискретное преобразование Фурье. Результат можно получить, осуществив численное интегрирование при t=0…
по формуле
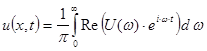. (15)
На АФЧХ (см. рис. 2) существенно себя проявляет только один видимый виток. Поэтому следует взять один член ряда (15). Из графиков на рисунке 3 видно, насколько точное решение (9) и решение по формам колебаний (11) совпадает с предлагаемым частотным решением. Погрешность не превышает 18 %. Полученное расхождение объясняется тем, что решения (9) и (11) не учитывают рассеяние энергии в материале стержня.
Рис. 3. Переходный процесс для конца стержня; 1, 2, 3 - графики, построенные соответственно по формулам (9), (11), (15).
В качестве более сложного примера рассмотрим задачу о продольных колебаниях ступенчатого стержня (рис. 4) с грузом на конце, соударяющегося с жестким препятствием со скоростью V0 , причем пусть масса груза равна массе прилегающего участка стержня:
.
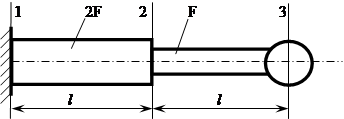
Рис. 4. Расчетная схема продольных колебаний ступенчатого стержня с грузом на конце
Введем характерные сечения 1,2,3 стержня, в которых будем вычислять перемещения. Составим систему разрешающих уравнений:
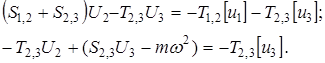(16)
В результате решения системы (16) получим графики АФЧХ (рис. 5) для перемещений во втором и третьем сечениях (U2 () и U3() соответственно). Вычисления производились при следующих значениях постоянных: l = 2 м; E = 2.1×1011 Па; F = 0.06 м2; 
= 7850 кг/м3; V = 10 м/с. На полученных АФЧХ существенно себя проявляют лишь два видимых витка. Поэтому при построении переходного процесса в выбранных сечениях возьмем два члена ряда (16). Для этого предварительно необходимо определить
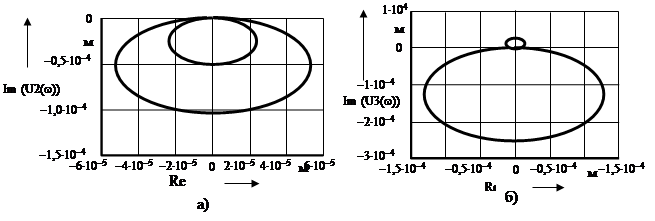
Рис. 5. АФЧХ перемещений во втором и третьем сечении ступенчатого стержня (см. рис. 4)
Аналогично по формуле (15) строится переходный процесс.
Вывод: разработан метод расчета продольных колебаний стержней при соударении с препятствием.
Рецензенты:
Лебедев А.М., д.т.н., доцент, профессор Ульяновского высшего авиационного училища (института), г. Ульяновск.
Антонец И.В., д.т.н., профессор Ульяновского государственного технического университета, г. Ульяновск.