Системный подход к решению задач управления транспортной инфраструктурой большого города обеспечивается разработкой и использованием интеллектуальных транспортных систем (ИТС). Анализ российского и зарубежного опыта проектирования и развития ИТС, принципов их интеграции, использования при осуществлении грузовых и пассажирских перевозок, при управлении транспортными потоками (ТрП) в различных транспортных ситуациях позволяет сделать вывод о целесообразности использования ИТС на автомобильном транспорте.
Термин «Интеллектуальные транспортные системы» характеризует комплекс интегрированных средств управления транспортной инфраструктурой (улично-дорожной сетью, техническими средствами организации дорожного движения, транспортными потоками), применяемых для решения задач организации дорожного движения, на основе современных информационных технологий, организации информационных потоков о функционировании транспортной инфраструктуры в реальном режиме времени [1].
Цели создания и внедрения ИТС приведены на рисунке 1.
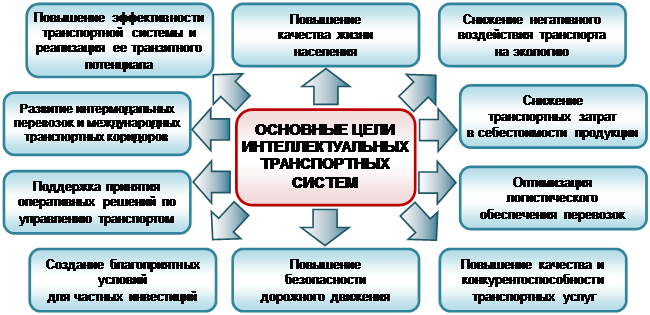
Рисунок 1. Основные цели интеллектуальных транспортных систем
Эффекты от внедрения ИТС
Преимущества и плюсы внедрения ИТС:
- для водителей
- более высокая безопасность – значительно меньший риск ДТП;
- уменьшение времени и стоимости проезда;
- более высокий уровень комфортности управления транспортными средствами и информированности, улучшение прогнозируемости времени проезда.
- для окружающей среды
- уменьшение шума и выбросов в атмосферу за счет более плавного изменения скорости транспортного потока и движения с постоянной скоростью.
- для национальной экономики
- уменьшение потерь из-за ДТП;
- снижение потерь, связанных с загрязнением окружающей среды;
- уменьшение потерь, связанных с пробками;
- улучшение использования существующей дорожной сети.
- для организаций, обслуживающих дорогу,
- улучшение планирования ресурсов, особенно обслуживания в период зимы, а также для обоснованного прогноза дорожных работ.
Показательными являются эффекты, полученные для кольцевой автомагистрали в районе Мюнхена. После ввода ИТС на этом автобане получены данные, которые при сравнении предшествующего и последующего 3-летних периодов показали:
- уменьшение длины заторов на 67 %;
- снижение числа ДТП на 35 %;
- снижение числа ДТП с пострадавшими на 31 %;
- снижение числа пострадавших при ДТП на 30 %.
Проект в Хессене:
- уменьшениечисла серьезных инцидентов на 30 %;
- уменьшение времени в пути на 20 %;
- увеличение пропускной способности на 25 %.
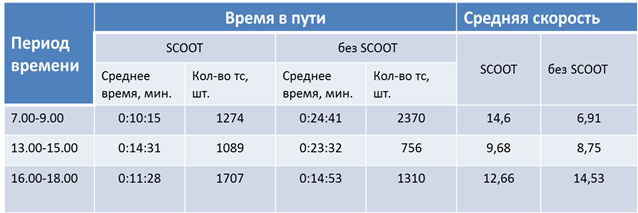
В таблице 1 приведены данные по результатам внедрения ИТС на примере SCOOT. В результате исследований по сравнению SCOOT с обычными системами он показал уменьшение задержек транспортных средств на 12 % в Глазго и 27 % в Ковентри. Сравнение проводилось через день на различных участках, включая плотную городскую сеть в центре Глазго и радиальную дорожную сеть в Ковентри. В Торонто SCOOT продемонстрировал уменьшение задержек транспорта на 14 % над системами с календарной автоматикой. В вечернее время и в субботу задержки уменьшились до 21 % и 34 %, соответственно. При проведении массовых мероприятий задержки уменьшились до 61 %, что демонстрировало устойчивость SCOOT к необычным событиям. Было также оценено, что внедрение ИТС сократило затраты на обновление программ координации в 30 человеко-лет.
Таблица 1. Результаты внедрения SCOOT
Модели транспортных потоков
Разработка и исследование эффективности различных методов управления транспортными потоками в рамках ИТС требует знания закономерностей их поведения на улично-дорожной сети (УДС) города – интенсивности движения, плотности, распределения интервалов между транспортными средствами (ТрС) в потоке в заданном сечении, времени проезда по некоторому участку УДС, транспортных задержек и др.
Одним из главных направлений теоретических и экспериментальных исследований в теории транспортных потоков в течение многих лет является изучение зависимостей между основными характеристиками ТрП. Несмотря на это, до настоящего времени не устранены некоторые противоречия между реальными данными и теоретическими предпосылками в основных моделях транспортного потока:
- рассеивание фактических данных параметров дорожного движения и детерминированные соотношения в макромоделях;
- постоянное значение отношения критической
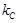 и максимальной
и максимальной 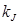 плотности ТрП
плотности ТрП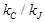 для каждой из моделей и переменное значение отношения
для каждой из моделей и переменное значение отношения 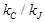 в реальном ТрП;
в реальном ТрП; - однотипность формы зависимости между параметрами транспортных потоков для каждой из моделей и изменение функциональной формы для реальных соотношений интенсивность – плотность, скорость – плотность;
- возможность разрывов между значениями характеристик ТрП при переходе от стабильного состояния к заторовому и гладкими соотношениями для теоретических макромоделей.
Характеристики транспортного потока
В рамках макроскопического подхода транспортный поток ![]() ,
, ![]() , движущийся по улично-дорожной сети – дугам
, движущийся по улично-дорожной сети – дугам ![]() орграфа G, характеризуется общей средней скоростью v, плотностью потока k и интенсивностью движения I в определенный момент времени в определенной точке УДС.
орграфа G, характеризуется общей средней скоростью v, плотностью потока k и интенсивностью движения I в определенный момент времени в определенной точке УДС.
На основе исследований дорожного движения и практики его организации выработаны многочисленные измерители и критерии. К наиболее часто применяемым показателям относятся:
- интенсивность движения I, авт./ч; авт./сут.;
- плотность транспортного потока k, авт./м, авт./км;
- скорость движения v, км/ч; м/с;
- продолжительность задержки движения D, с;
- состав транспортного потока
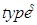 .
.
Транспортный поток ![]() определен типом транспортных средств, составляющих его:
определен типом транспортных средств, составляющих его:
![]()
![]() ,
,
т.е. тип ТС: ![]() ; где каждому типу поставлено в соответствие число: «велосипед» –1, «мотоцикл» – 2, «гужевая повозка» – 3, «легковой автомобиль» – 4, «грузовик 1» – 5, «грузовик 2» – 6, «грузовик 3» – 7, «автобус» – 8, «троллейбус» – 9, «автопоезд» – 10.
; где каждому типу поставлено в соответствие число: «велосипед» –1, «мотоцикл» – 2, «гужевая повозка» – 3, «легковой автомобиль» – 4, «грузовик 1» – 5, «грузовик 2» – 6, «грузовик 3» – 7, «автобус» – 8, «троллейбус» – 9, «автопоезд» – 10.
Для приведения неоднородного по составу потока к «однородному», состоящему только из легковых транспортных средств, для каждого типа ТрС определен коэффициент приведения ![]() . Для легкового автомобиля
. Для легкового автомобиля ![]() , для мотоцикла –
, для мотоцикла – ![]() и т.д. Коэффициент
и т.д. Коэффициент ![]() для разных типов грузовых ТрС определен их грузоподъемностью и варьируется от 1.7 для типа ТрС=«грузовик 1» до 3.5 для типа ТрС=«грузовик 3».
для разных типов грузовых ТрС определен их грузоподъемностью и варьируется от 1.7 для типа ТрС=«грузовик 1» до 3.5 для типа ТрС=«грузовик 3».
Движение транспортных средств на перекрестке канализируется и подразделяется на право-, левоповоротные и прямые потоки, регламентированные направлениями соответствующих дуг графа УДС и установленными дорожными знаками. Интенсивность соответствующих потоков является весовыми характеристиками дуг.
Макроскопические модели движения транспортного потока
В процессе развития макроскопических моделей транспортного потока, полученных в рамках классического подхода с использованием детерминированных зависимостей между интенсивностью, плотностью и скоростью транспортного потока, к моделям предъявлялись все новые требования в соответствии с уровнем задач организации движения и перевозок:![]() , где k и
, где k и ![]() – плотность потока и максимальная (заторовая) плотность потока, соответственно;
– плотность потока и максимальная (заторовая) плотность потока, соответственно;![]() – скорость свободного движения, т. е. максимально возможная скорость на участке дороги;
– скорость свободного движения, т. е. максимально возможная скорость на участке дороги;![]() – скорость кинематической волны при заторовой плотности;
– скорость кинематической волны при заторовой плотности; ![]() – совокупность безразмерных параметров. В качестве дополнительного параметра может выступать эквивалентная дистанция:
– совокупность безразмерных параметров. В качестве дополнительного параметра может выступать эквивалентная дистанция:![]() . При одной и той же плотности эквивалентная дистанция уменьшается с увеличением скорости, что в полной мере согласуется с требованиями обеспечения безопасности движения, поскольку фактическая дистанция остается неизменной, а эквивалентная дистанция уменьшается, свидетельствуя об усложнении ситуации.
. При одной и той же плотности эквивалентная дистанция уменьшается с увеличением скорости, что в полной мере согласуется с требованиями обеспечения безопасности движения, поскольку фактическая дистанция остается неизменной, а эквивалентная дистанция уменьшается, свидетельствуя об усложнении ситуации.
Рассмотрим зависимости следующих типов: линейная, логарифмическая, экспоненциальная, степенная, регрессионная, разрывная, вероятностная на основе распределения скорости.
Линейная зависимость между плотностью транспортного потока k и его скоростью v. Линейная зависимость впервые была предложена Гриншилдсом, выражается уравнением (1), впоследствии доработана Ричардсом (2):
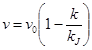 и
и 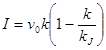 , (1)
, (1)
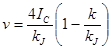 и
и ![]() . (2)
. (2)
При высоких значениях скорости свободного движения ![]() применение модели Гриншилдса для определения пропускной способности приводит к завышенным результатам. Для однородного потока из легковых автомобилей при максимальной плотности ТП kJ =140÷160 авт/км и скорости при уровне пропускной способности vС =45 км/час пропускная способность достигает 1800÷2000 авт/час. Расчетные значения пропускной способности для этих условий по модели Гриншилдса составляют 3150÷3600 авт/час. Степень соответствия расчетных и экспериментальных данных в модели Ричардса, так же, как и в модели Гриншилдса, повышается при снижении скорости свободного движения [4].
применение модели Гриншилдса для определения пропускной способности приводит к завышенным результатам. Для однородного потока из легковых автомобилей при максимальной плотности ТП kJ =140÷160 авт/км и скорости при уровне пропускной способности vС =45 км/час пропускная способность достигает 1800÷2000 авт/час. Расчетные значения пропускной способности для этих условий по модели Гриншилдса составляют 3150÷3600 авт/час. Степень соответствия расчетных и экспериментальных данных в модели Ричардса, так же, как и в модели Гриншилдса, повышается при снижении скорости свободного движения [4].
Логарифмический тип зависимости имеют макромодели Гринберга (3) и Эл–Хозаини (4). Модель Гринберга описывается уравнениями:
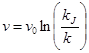 и
и 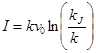 , (3)
, (3)
и при достижении пропускной способности ![]() . Значение нормированной плотности
. Значение нормированной плотности ![]() всегда равно 0.368 при максимальной интенсивности движения. Недостатком модели является то, что при плотности, стремящейся к нулю, расчетные значения скорости превышают скорость свободного движения:
всегда равно 0.368 при максимальной интенсивности движения. Недостатком модели является то, что при плотности, стремящейся к нулю, расчетные значения скорости превышают скорость свободного движения:
![]() и
и ![]() . (4)
. (4)
Максимальная интенсивность движения достигается при нормированной плотности ![]() =0.60371 и определяется как
=0.60371 и определяется как ![]() . Модель Эл–Хозаини дает достоверные результаты при высокой плотности и скорости транспортного потока менее 17 км/час.
. Модель Эл–Хозаини дает достоверные результаты при высокой плотности и скорости транспортного потока менее 17 км/час.
В макромоделях, основанных на экспоненциальной зависимости между скоростью и плотностью и представленных моделями Андервуда (5), Дрейка (6), Зырянова (7), при высокой плотности движения (![]() ) расчетные значения интенсивности превышают фактические:
) расчетные значения интенсивности превышают фактические:
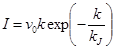 , (5)
, (5)
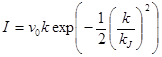 , (6)
, (6)
![]() . (7)
. (7)
Модель (4) дает достоверный результат только на участке насыщения.
Наиболее известные степенные модели Пайпса (8) и Д. Дрю (9) позволяют за счет коэффициента пропорциональности n трансформировать форму зависимости между плотностью и скоростью, приспосабливаясь к конкретным экспериментальным данным.
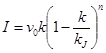 , (8)
, (8)
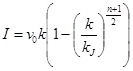 . (9)
. (9)
При n=1 уравнение (1) является частным случаем (9).
Усложнение макромодели ТрП за счет введения дополнительных параметров (10) позволяет исследовать поведение транспортного потока в критических точках – насыщения ТрП и затора.
В качестве дополнительного параметра возьмем время прохождения участка УДС, равного длине автомобиля, движущегося со скоростью свободного движения: ![]() , тогда основные характеристики ТрП при уровне пропускной способности будут определены следующим образом:
, тогда основные характеристики ТрП при уровне пропускной способности будут определены следующим образом:
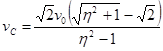 ,
,
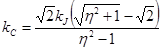 ,
,
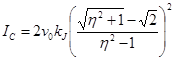 . (10)
. (10)
Основная диаграмма транспортного потока, построенная по модели (10) для экспериментальных данных, полученных автором, представлена на рисунке 2.
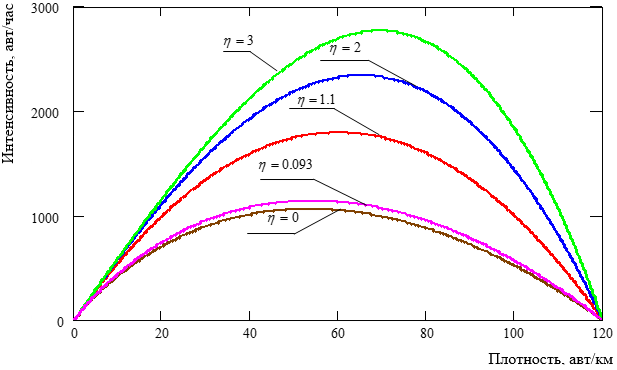
Рисунок 2. Основная диаграмма транспортного потока
Рецензенты:
Титов Б.А., д.т.н., профессор, заведующий кафедрой организации и управления перевозками на транспорте, ФГБОУ ВПО «Самарский государственный аэрокосмический университет имени академика С.П. Королева (национальный исследовательский университет)», г. Самара.
Хайтбаев В.А., д.э.н., профессор кафедры организации и управления перевозками на транспорте, ФГБОУ ВПО «Самарский государственный аэрокосмический университет имени академика С.П. Королева (национальный исследовательский университет)», г. Самара.



