Системы пневмотранспорта с камерными насосами (КН) являются одними из самых распространённых в России. Широкое применение таких типов насосов определяется их высокими эксплуатационными характеристиками по сравнению с другими системами пневмотранспорта [1, 2, 3, 5]. Однако из-за особенностей их конструкции применение камерных насосов связано с низкой энергоэффетивностью.
На промышленных предприятиях также есть проблема применения систем пневмотранспорта с камерными насосами, которая заключается в «просадке» давления в сети воздухоснабжения при их работе. Поэтому существует необходимость разработки новых конструкций КН для решения вышеуказанных проблем.
Для разработки энегоээффективных режимов работы и конструкции камерных насосов
применен метод математического моделирования. Математическое моделирование позволяет, без материальных затрат на натурные испытания, проверить влияние различных факторов на производительность КН (расход, давление, температура воздуха, конструкция и т.д).
Математическая модель движения двухфазного потока основана на модели Эйлера [4] и состоит из системы дифференциальных уравнений:
– переноса импульса твердой фазы
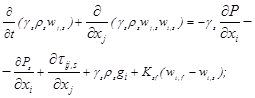 (1)
(1)
– переноса импульса флюида
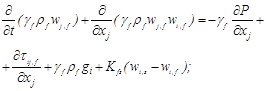 (2)
(2)
– неразрывности для твердой фазы
![]() (3)
(3)
– неразрывности для флюида
![]() (4)
(4)
– уравнение сохранения энергии
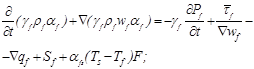 (5)
(5)
где ![]() – тензор напряжений твердой фазы;
– тензор напряжений твердой фазы; ![]() – тензор напряжений флюида; P – давление;
– тензор напряжений флюида; P – давление; ![]() – относительная объемная концентрация;
– относительная объемная концентрация; ![]() – плотность;
– плотность; ![]() – скорость;
– скорость; ![]() – символ Кронекера;
– символ Кронекера; ![]() – коэффициент взаимодействия частиц твердой фазы с флюидом;
– коэффициент взаимодействия частиц твердой фазы с флюидом; ![]() – тепловой поток;
– тепловой поток; ![]() – коэффициент теплоотдачи;
– коэффициент теплоотдачи; ![]() – источниковый член; F – площадь поверхности твердой фазы, индексы s и f – твердая фаза и флюид соответственно.
– источниковый член; F – площадь поверхности твердой фазы, индексы s и f – твердая фаза и флюид соответственно.
Для описания турбулентных свойств двухфазного потока принята k-ε модель турбулентности.
Система дифференциальных уравнений (1) – (5) решена при помощи программно-вычислительного комплекса Ansys Fluent.
Целью математического моделирования работы камерного насоса «Монжус» была оценка влияния длины выходного патрубка насоса на потери давления и производительность камерного насоса. Так, уменьшение потерь давления приводит к уменьшению затрат на перемещение материала и, следовательно, приводит к уменьшению энергозатрат на привод компрессора.
Все расчеты были выполнены для следующих исходных данных:
- материал – цемент со средним размером частиц 15,5 мкм;
- расход воздуха 1,2 кг/с;
- уровень материала в насосе 1 м.
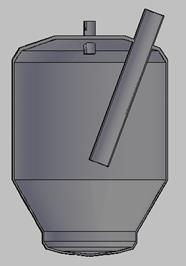
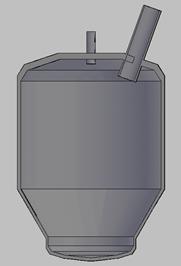
Конструкции камерного насоса приведены на рис. 1 и 2.

а) Общий вид насоса б) фронтальный разрез
Рис. 1. Конструкция камерного насоса «Монжус»
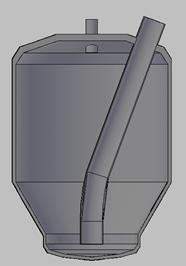
а) R=H б) R=2/3H в) R=0,1H
Рис. 2. Конструкции камерных насосов для расчета (3D-разрез)
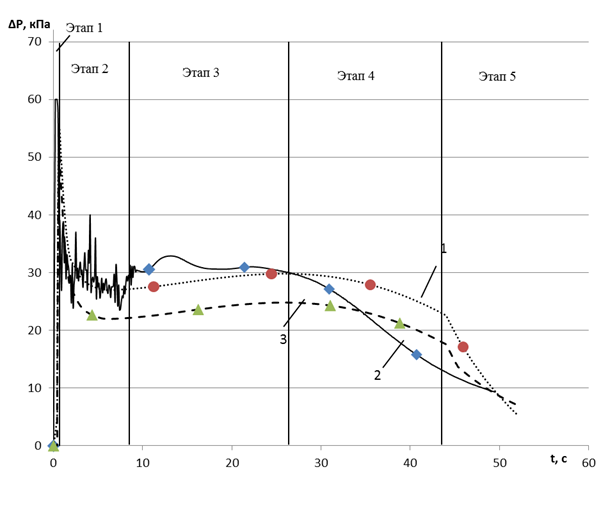
1 – R=H; 2 – R=2/3H; 3 – R=0,1H
Рис. 3. Потери давления в камерном насосе
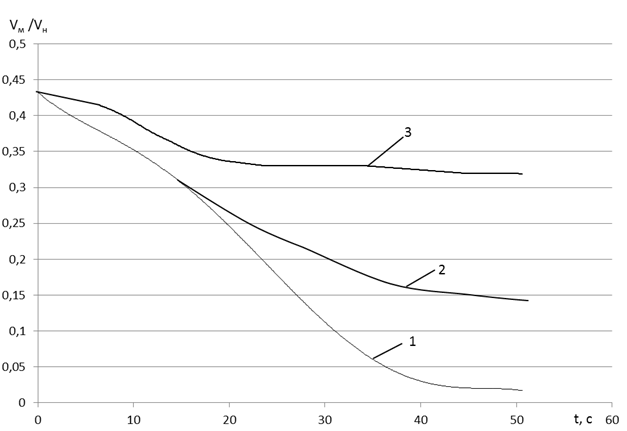
1 – R=H; 2 – R=2/3H; 3 – R=0,1H
Рис. 4. Изменение объемной концентрации материала в камере насоса
В качестве параметров оптимизации были выбраны потери давления воздуха (ΔP) и удельный расход материала (Vм/Vн). Результаты расчета приведены на рис. 3 и 4. Как видно при уменьшении длины патрубка уменьшаются потери давления в КН. Однако в этом случае скорость опорожнения камеры насоса уменьшается, а, следовательно, увеличивается остаток материала в камере и соответственно снижается производительность насоса.
Анализируя результаты расчета потерь давления (рис. 3), цикл разгрузки камерного насоса можно условно разделить на 5 этапов.
Этап 1. Наблюдается резкое увеличение потерь давления из-за затрат энергии потока воздуха на псевдоожижение материала. Длительность этого процесса для различных конструкций КН равна 0,5–1 с.
Этап 2. На данном этапе работы КН начинается фильтрация воздуха через сыпучий материал, поэтому наблюдается снижение потерь давления. Отметим, что для конструкции насоса, изображенного на рис. 2 б, на этом этапе наблюдается нестабильность изменения потерь давления, что может привести к аварийному режиму его работы из-за возможного образования пробок материала. Длительность этапа находится в интервале 7–9 с.
Этап 3. На этом этапе наблюдается незначительный рост потерь давления (не более
5 кПа). Это происходит из-за роста скорости материала в выходном патрубке. Длительность этапа ~20 с.
Этап 4. На четвертом этапе потери давления начинают уменьшаться. Это связано с уменьшением объемной концентрации в выходном патрубке КН. Длительность этапа
~15 с.
Этап 5. На этом этапе разгрузка КН практически прекращается, что приводит к еще более быстрому уменьшению потерь давления. Длительность этапа ~10 с.
Анализируя данные расчета, можно сделать вывод о том, что наименьшие потери давления у конструкции КН, изображённом на рис. 2 в, но в этом случае в камере насоса остается более 73 % материала.
Конструкция КН рис. 2 б по сравнению с конструкцией рис. 2 а тоже работает с меньшими потерями давления, и по окончанию процесса в камере насоса остается менее 30 % материала. Однако следует отметить, что потери давления в начальный момент времени выше на 10 %, а также наблюдается нестабильность на начальном этапе работы. Это может привести к образованию пробки в материалопроводе и как следствие к аварийному режиму работы КН.
Результаты расчета потерь давления соответствуют показаниям штатных приборов, установленных на ОАО «Бонолит строительные системы» (г. Старая Купавна) и ОАО «ЭКО» (г. Ярославль).
Выводы
- Разработана математическая модель пневмотранспорта сыпучих материалов, учитывающая размеры частиц, сжимаемость газа, взаимодействие частиц друг с другом, с газом и стенкам материалопровода.
- С уменьшением длины патрубка уменьшаются потери давления, но в этом случае наблюдается увеличение количества остатка материала в камере. Следовательно, уменьшение длины патрубка КН не целесообразно.
- Разработанная математическая модель движения двухфазных потоков
позволяет исследовать режимы работы камерных насосов не только с верхней разгрузкой материала, но и других конструкций камерных насосов.
Рецензенты:
Авдюнин Е.Г., д.т.н., профессор кафедры «Промышленная теплоэнергетика» ИГЭУ, Ивановский государственный энергетический университет, г. Иваново.
Бушуев Е.Н., д.т.н., заведующий кафедрой автоматизации технологических процессов, Ивановский государственный энергетический университет, г. Иваново.



