Введение
Успешность формирования у обучаемых системы научных знаний в соответствующей научной области (в нашем случае – математики), в первую очередь, зависит от умений учителя организовать работу по изучению понятий и их определений. Однако определения математических понятий содержат лишь логически независимые свойства понятия. Остальные свойства логически зависимы от основного содержания и приводятся учащимся в виде математических предложений – теорем, которые в том числе выражают отношения между понятиями. Таким образом, теоремы пронизывают все разделы математики, делают ее единой наукой. Поэтому обучение этому понятию – одна из главных задач методики преподавания математики. Целью исследования, о котором идет речь в данной статье, является формирование у будущих учителей математики умений работать с теоремами средствами курса математической логики.
Процесс изучения теоремы начинается с понимания ее структуры. Только уяснив структуру и содержание теоремы, можно переходить к её доказательству. Уяснение структуры теоремы приводит к пониманию ассоциированных с ней утверждений – обратного, противоположного, обратного противоположному, что в свою очередь служит отправным пунктом к пониманию методов доказательства теорем, использованию их в решении задач и доказательствах других теорем.
Теоремы школьного курса формулируются в основном в импликативной форме. В символах математической логики – 
, где х может быть как переменной, так и упорядоченным набором переменных, т.е. 
.
Отметим, что логическая структура предикатов 
и 
имеет вариативный характер. Далингер В.А. [1] приводит целый ряд логических структур теорем, имеющих импликативную форму:
1) 
. Например, «если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник параллелограмм». В символической записи теоремы 
– множество четырехугольников, 
: ’в четырехугольнике 
диагонали пересекаются’ и 
: ’в четырехугольнике диагонали точкой пересечения делятся пополам’ и : ’четырехугольник – параллелограмм’.
2) 
. Например, «если запись натурального числа оканчивается цифрами 0 или 5, то это число делится без остатка на 5». В символической записи теоремы – множество натуральных чисел, 
:’запись натурального числа х оканчивается цифрой 0’, : ’запись натурального числа оканчивается цифрой 5’ и :’ натуральное число без остатка делится на 5’.
3) 
. Например, «у параллелограмма противолежащие стороны равны, противолежащие углы равны». В символической записи теоремы – множество четырехугольников, 
: ’четырехугольник – параллелограмм’, 
: ’в четырехугольнике противолежащие стороны равны’ и 
: ’в четырехугольнике противолежащие углы равны’.
4) 
. Например, «в ромбе диагонали перпендикулярны друг другу и делят углы ромба при вершинах пополам». В символической записи теоремы – множество четырехугольников, :’четырехугольник 
– ромб’, 
: ’в четырехугольнике диагонали перпендикулярны’ и 
:’в четырехугольнике диагонали делят вершины углы при вершинах пополам’.
5) 
. «Если для любых 
и 
из некоторого промежутка из того, что 
следует 
, то 
не возрастает на данном промежутке». В символической записи теоремы – множество пар 
чисел, каждое из которых принадлежит указанному промежутку, 
: ’ ’, 
: ’’ и : ’ не возрастает на указанном промежутке’.
6) 
. «Если функция является возрастающей на некотором промежутке, то для любых и из этого промежутка из того, что следует 
». В символической записи теоремы – множество пар чисел, каждое из которых принадлежит указанному промежутку, :’ является возрастающей на указанном промежутке’, : ’ ’ и : ’’.
В приведенных выше примерах предикаты и были равносильны либо дизъюнкции, либо конъюнкции, либо импликации некоторых предикатов, причем, очевидно, что количество дизъюнктивных и конъюнктивных членов может быть любым конечным числом.
Как отмечает Игошин В.И. [2], помимо теорем, записанных в импликативной форме, встречаются и теоремы иного типа:
1) 
. Например, 
.
2) 
. «Через любую точку проходит прямая, перпендикулярная к данной прямой, и притом только одна». В символической записи теоремы – точка, 
– прямая, 
: ’единственная прямая , которая проходит через точку , перпендикулярно данной прямой’.
Согласно Стефановой Н.Л. [5], работа с теоремой начинается с проведения учителем логико-математического анализа теоремы, а именно – установления формы формулировки теоремы; перевода формулировки, если необходимо, в импликативную форму; записи структуры, т.е. вычленения разъяснительной части, условия, заключения с выделением простых высказываний и содержания структурных элементов; определения вида (простая или сложная); формулирования утверждений обратного данному, противоположного данному и обратного противоположному (определения их истинности или ложности).
Выделим методические умения, относящиеся к работе с теоремой, предварительно разделив их на две группы.
К первой будем относить методические умения работать со структурой формулировки теоремы:
- умение выполнять логический анализ формулировки теоремы;
- умение записывать формулировку теоремы на языке математической логики;
- умение преобразовывать логическую структуру формулировки теоремы, в том числе с целью перевода в импликативную форму;
- умение проверять формулировку теоремы на соответствие требованиям корректности к ней;
- умение выделять необходимые и достаточные условия теоремы;
- умение формулировать утверждения: обратное, противоположное и обратное противоположному (определять их истинностное значение).
Вторую группу составляют умения, относящиеся к организации процесса изучения теоремы. А именно, умения подбирать или составлять задачи в соответствии с целями этапов изучения теоремы: работа по открытию факта, о котором идет речь в теореме, формулировка теоремы, поиск доказательства и пр.
Выделим систему задач как основное средство формирования методических умений работать с теоремами у бакалавров педагогического образования по профилю «Математика» на занятиях по математической логике.
Указанная система задач обладает рядом особенностей. Первая – использование парных задач: одна задача нацелена на формирование методических умений работать со структурой теоремы, вторая – на конструирование задач для организации процесса изучения теоремы. Вторая особенность – использование материала из различных школьных учебников по алгебре и геометрии, а также материалов из различных разделов высшей математики, в том числе курса математической логики.
В данной статье приведем примеры задач курса математической логики, классифицированных в соответствии с некоторыми из выделенных умений, относящихся к работе с теоремами.
Задачи на формирование умения проводить логический анализ формулировки теоремы. Выполняя логический анализ формулировки теоремы, необходимо выделить:
- разъяснительную часть, т.е. 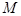– множество объектов, на котором рассматривается теорема;
- простые высказывания, составляющие условие и заключение теоремы;
- логические связки между указанными простыми высказываниями (конъюнкция, дизъюнкция, импликация) или относящиеся к ним (отрицание, кванторы всеобщности или существования);
- логические связки между условием и заключением теоремы (импликация, эквиваленция).
С целью формирования умения проводить логический анализ формулировки теоремы обучающимся могут быть предложены, например, следующие задачи.
Задача 1 (тема «Область истинности предиката»). В предложении вместо пропусков вставить одно из указанных слов с целью получения истинного высказывания (0-местного предиката):
Для любых ___ (действительных, положительных действительных, неотрицательных действительных) чисел 
и 
справедливо равенство 
.
Решение задач подобного рода сопряжено с выделением из формулировки теоремы ее разъяснительной части. Довольно часто студенты вообще опускают эту часть теоремы, что снижает уровень их профессиональной подготовки.
Задача 1’. Составить задачи на нахождение/выделение обучающимися области истинности предиката, используя материалы из школьного учебника по теме: «Свойства логарифмической функции».
Задача 2 (тема «Операции над предикатами»). В предложении вместо пропусков вставить одну из указанных логических связок с целью получения истинного высказывания (тождественно истинного 0-местного предиката):
Плоскость, пересекающая пирамиду ___ (и, или) параллельная ее основанию, отсекает подобную пирамиду.
Отметим, что в задачах подобного рода студентам можно предложить самостоятельно выделить множество, на котором задан предикат, т.е. разъяснительную часть теоремы.
Задача 2’. Составить задачи на выделение обучающимися логических связок в формулировках теорем по теме: «Четырехугольники».
Задача 3 (тема «Операции над предикатами»). В записи следующего предиката выделить элементарные: Средняя линия треугольника, соединяющая середины двух данных сторон треугольника, параллельна третьей стороне и равна ее половине.
Очевидно, что союз «и» указывает на конъюнкцию двух элементарных предикатов 
и 
, которая составляет заключение теоремы, а предикат 
является условием теоремы, где
:’ Средняя линия треугольника, соединяющая середины двух данных сторон треугольника’;
:’ Средняя линия треугольника параллельна третьей стороне треугольника’;
:’ Средняя линия треугольника равна половине третьей стороны’.
Задача 3’. Составить задачи на выделение в предикате элементарных предикатов и логических связок между ними в формулировках теорем по теме: «Четырехугольники».
Вышеприведенные примеры задач могут быть использованы обучающимися в разделе «Логика предикатов» курса математической логики.
Задачи на формирование умения записывать формулировку теоремы на языке математической логики. Студентам можно предложить записать формулировки двух утверждений на языке математической логики, одно из которых является теоремой, а другое – примером использования этой теоремы. Например: а) поскольку число делится и на 2, и на 3, то оно делится на 6; б) поскольку число 22734 делится и на 2, и на 3, то оно делится на 6.
Предложение а) имеет вид 
и является 0-местным предикатом, где : ’целое число делится на 2’, : ’целое число делится на 3’, : ’целое число делится на 6’. Предложение б) имеет следующую структуру: 
, где 
: ’ 22734 делится на 2’, 
: ’ 22734 делится на 3’, 
: ’ 22734 делится на 6’.
Существенным отличием в выявлении логической структуры предложения а) является необходимость восполнения разъяснительной части теоремы (множество всех целых чисел) и квантора всеобщности (для любого целого числа ).
Для формирования данного умения могут быть использованы логические текстовые задачи, решение которых требует их перевода на язык математической логики, а также задания вида: «Записать следующее математическое утверждение на языке алгебры высказываний/логики предикатов».
Задачи на формирование умения преобразовывать логическую структуру формулировки теоремы, в том числе с целью перевода в импликативную форму. Уяснив теорему, можно выражать её в различных формулировках, имеющих разную логическую структуру [2]. Одинаковость содержания доказывает эквивалентность формулировок теорем. Необходимость данного умения определяется тем, что:
1) процедура равносильного преобразования формулировок теорем помогает рассмотреть одну и ту же по существу теорему с различных логических точек зрения;
2) импликативная форма более доступна для разбора учащимися структуры теоремы. Таким образом, учитель математики должен уметь переводить формулировку теоремы из категоричной или разделительной форм в условную (импликативную);
3) существует множество школьных учебников по алгебре и геометрии, в которых по-разному формулируются одни и те же теоремы по содержанию (смыслу);
4) учитель математики обязан уметь выявлять и исправлять ошибки учащихся при формулировании теорем, в основе чего лежит умение доказывать/опровергать эквивалентность теорем.
Целью решения следующих задач является формирование указанного умения:
Задача 4. Предварительно записав следующие утверждения на языке логики предикатов, докажите их эквивалентность:
1) Если натуральное число делится и на 2, и на 5, то оно делится на 10.
2) Если натуральное число кратно 2, то из кратности его числу 5 следует, что данное число кратно 10.
Решение. Введем следующие обозначения одноместных предикатов, заданных на множестве натуральных чисел: : ’ делится на 2’, : ’ делится на 5’, : ’ делится на 10’. Согласно введенным обозначениям предложения 1) и 2) имеют следующие структуры 
и 
соответственно. Проверим равносильность формул:
.
Задача 4’. Составить задачи на доказательство эквивалентности формулировок теоремы, используя материалы школьных учебников по алгебре и геометрии.
Задачи на формирование умения выделять необходимые и достаточные условия теоремы. К типичным ошибкам студентов при работе с теоремами можно отнести «подмену» понятий необходимого и достаточного условий. Например, условие «две прямые в пространстве не пересекаются» является необходимым, но не достаточным условием «параллельности прямых в пространстве», поэтому его нельзя использовать в качестве единственного условия в определении «параллельных прямых в пространстве». С другой стороны, «принадлежность векторов одной прямой» является достаточным условием их «коллинеарности», но не является необходимым, поскольку коллинеарность векторов не влечет их принадлежности одной прямой. Для учителя математики важно уметь безошибочно определять необходимость и достаточность какого-либо условия, в том числе и для грамотного построения собственных высказываний.
Формировать указанное выше умение у будущего учителя математики можно через решение следующих задач по теме: «Применение логики предикатов к логико-математической практике»:
Задача 5. В предложениях вместо пропусков вставить «необходимо» или «достаточно» с целью получения истинного высказывания (в скобках указаны верные ответы):
а) Для параллельности прямых в пространстве ……………, чтобы они не пересекались (необходимо);
б) Для равносильности двух систем …………….., чтобы каждое решение одной из них было решением и второй (достаточно).
Задача 5’. Используя материалы школьного курса алгебры по теме: «свойства функций», составьте задачи на выявление необходимых и достаточных условий теоремы.
Задачи на формирование умения формулировать утверждения: обратное, противоположное и обратное противоположному (определять их истинностное значение).
Связь между теоремами (прямая теорема эквивалентна обратной противоположной, а обратная теорема – противоположной) показывает нецелесообразность изучения всех четырех в школьном курсе математики, достаточно прямой и обратной, но не отменяет их применения для уяснения учащимися структуры теоремы, при решении задач.
Для формирования данного умения студентам можно предложить задания вида: «Сформулируйте утверждения, ассоциированные с данным, предварительно переведя его на язык математической логики». В качестве предложений можно взять теоремы из школьных курсов алгебры и геометрии, записанные в категоричной или разделительной форме. В ходе решения задачи студент должен будет перевести теорему в условную форму, выделив разъяснительную часть, элементарные предикаты и восполнив все логические связки, затем записать теорему на языке математической логики, произвести необходимые равносильные преобразования формулы и только потом сформулировать предложения (истинные или ложные), ассоциированные с данным.
Согласно концепции профессионально-педагогической направленности обучения математике будущих учителей (Мордкович А.Г. [4]), каждый предмет, изучаемый в ВУЗе, должен вносить вклад в решение проблемы совершенствования подготовки будущих учителей.
Однако анализ педагогической действительности позволил сделать вывод о «ненацеленности» курса математической логики на формирование «методических» умений будущих учителей математики. В частности, деятельность студентов направлена на реализацию предметных целей курса, например, «изучить понятие высказывания», «изучить понятие предиката» и пр. Как следствие, они не осознают значения дисциплины для формирования профессиональной компетентности.
На наш взгляд, курс математической логики обеспечит формирование профессиональных умений (в том числе, умений работать с теоремами), если будет структурирован через системы задач, особенности которых описаны выше.
Результаты данного исследования представлены в содержании практикума курса математической логики, включенного в учебно-методический комплекс по данной дисциплине, в Волгоградском государственном социально-педагогическом университете.
Рецензенты:
Сергеев А.Н., д.п.н., профессор кафедры информатики и информатизации образования ФГБОУ ВПО «Волгоградский государственный социально-педагогический университет», г. Волгоград.
Петрова Т.М., д.п.н., профессор кафедры информатики и информатизации образования ГБОУ ДПО «Волгоградская государственная академия повышения квалификации и переподготовки работников образования», г. Волгоград.