Введение
Отражение различной природы волн от поверхностей тел широко используется для дистанционного и бесконтактного исследования параметров и физических свойств этих тел. При отражении волн от движущейся границы раздела сред наблюдается изменение частоты отраженной по отношению к падающей волне, известное как эффект Доплера, рассматривавшийся многими авторами [1-5], преимущественно, в геометрических моделях волнового процесса. Этот эффект нашел широкое применение, в частности, для дистанционного измерения направления и величины скорости движущихся объектов. Зависимости коэффициентов отражения и прохождения, изменение частот отраженного и прошедшего сигналов от скорости движения самих сред, не рассматривались [3,4]. Вместе с тем, движение сред приводит к увлечению волнового процесса движущимися средами, как следствие, к невзаимности параметров сред для прямых и обратных волн и к существенному изменению физических свойств структур [5]. Рассмотрим здесь особенности отражения волн от подвижной границы раздела сред, каждая из которых может двигаться со своей скоростью.
Основные уравнения
Пусть плоская граница раздела двух сред движется со скоростью 
вдоль координатной оси 
(рис.1). Движение границы описывается уравнением: 
. Слева от границы расположена упругая среда с плотностью 
, характеризуемая скоростью распространения упругих волн - 
, справа - среда с соответствующими параметрами 
, 
. Пусть обе граничащие среды также движутся вдоль оси для общности со скоростями 
и 
соответственно. Тогда скорость распространения звуковых волн вдоль оси в первой среде равна 
, в противоположном направлении в той же среде скорость равна 
. Во второй среде с учетом условия на бесконечности волны распространяются вдоль оси со скоростью 
.
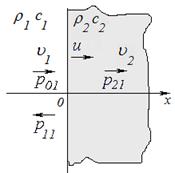
Рис.1. Отражение волн от подвижной границы раздела движущихся сред
Давление падающей волны представим в виде:
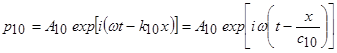. (1)
При взаимодействии волны с границей раздела сред образуются отраженная волна:
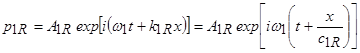, (2)
Прошедшая через границу раздела в другую среду волна описывается в виде:
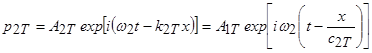. (3)
Здесь 
, 
, 
-частоты падающей, отраженной и прошедшей волн соответственно, 
, 
, 
- волновые числа, 
,
,
- амплитуды. Анализ граничных условий показывает: частоты отраженной 
, и прошедшей через границу раздела сред волн в общем случае отличаются от частоты падающей волны. Функции давления 
, 
, 
удовлетворяют волновому уравнению, а также должны удовлетворять граничным условиям на подвижной границе раздела сред, которые имеют вид:
, (4)
. (5)
Подстановка искомых решений (1)-(3) в первое граничное условие (4) дает соотношение:
.
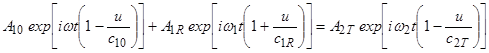Это соотношения должны выполняться для любого момента времени 
. Это можно обеспечить только при условии:
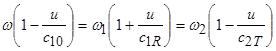. (6)
Отсюда частоты отраженной и прошедшей волн связаны с частотой падающей волны соотношениями:
, 
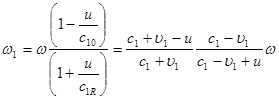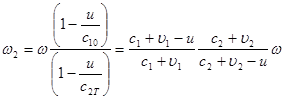. (7)
На рис. 2 показана зависимость отношения частоты отраженной волны к частоте падающей волны от относительной скорости движения границы раздела сред 
при различных относительных скоростях движения первой среды 
. Частота отраженной волны совпадает с частотой падающей волны при неподвижной границе раздела сред 
и уменьшается до нуля при увеличении скорости границы до скорости волн в первой среде (
) и мало зависит от параметра 
в области 
. Однако, в диапазоне скоростей 
наблюдается резонансный характер зависимости частоты отраженной волны. При этом с ростом 
интенсивное изменение частоты отраженной волны наблюдается при меньших значениях скорости границы 
.
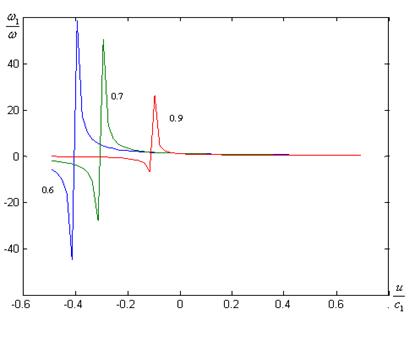
Рис.2. Зависимость относительной частоты отраженной волны 
от скорости движения границы раздела сред
В частном случае подвижной границы раздела и неподвижных сред из (7) имеем известные соотношения [1]:
, 
.
Характер зависимости частоты прошедших волн от скорости движения границы существенно зависит от отношения скоростей волн во второй и в первой средах 
. В интервале отрицательных (противоположное оси движение) скоростей частота монотонно растет до значений скорости границы раздела 
. При 
волновой процесс не догоняет границу раздела. На рис. 3 показана зависимость отношения частоты прошедшей волны 
к частоте падающей волны от относительной скорости движения границы раздела сред при отношении скоростей волн в средах с2/с1=0,8.
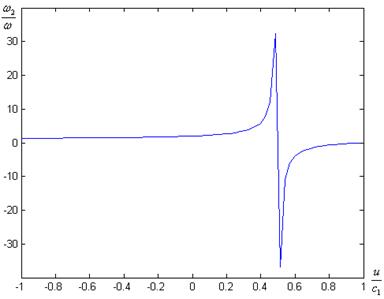
Рис.3. Зависимость относительной частоты отраженной волны 
от скорости движения границы раздела сред при с2/с1=0,8
Таким образом, частоты отраженной и прошедшей волн отличаются от частоты , падающей на границу раздела сред волны и зависят как от скорости движения границы раздела сред , так и от скоростей движения самих сред 
и 
.
Если граница движется в направлении распространения падающей волны (скорости и 
по направлению совпадают), то частота отраженного сигнала, как правило, меньше частоты падающей волны 
; если граница двигается навстречу падающей волне (скорости и 
противоположны по направлению), то 
. Однако, при некоторых соотношениях параметров возможно обратное соотношение частот. Частота прошедшего сигнала может быть больше или меньше в зависимости от соотношения скоростей сигнала в первой и второй средах: 
. При 
и скорости движения границы, меньшей скоростей волн в обеих средах: 
частота прошедшего сигнала 
.
Учет граничных условий (4), (5) при 
дает систему уравнений для определения амплитуд отраженной 
и прошедшей 
волн через амплитуду падающей волны 
:
,
.
Коэффициенты отражения и прохождения определяются выражениями:
, 
(8)
или с учетом скоростей движения границы 
и сред и :
, 
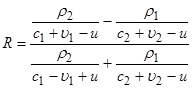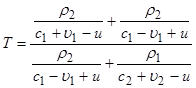. (9)
Из (8) следует, что условие отсутствия отраженного сигнала (
) приводит к соотношению:
,
которое выполняется при скорости движения границы раздела сред равной:
.
Рассмотрим частные случаи, представляющие практический интерес.
1) Если 
, движение границы раздела сред и движение самих сред отсутствуют. Коэффициент отражения принимает известный вид [1]:
.
2) Если 
, 
, движется только граница раздела сред. Коэффициенты отражения и прохождения определяются выражениями:
. 
.
Коэффициент отражения 
, при скорости движения границы:
.
3) Если 
, то вторая среда движется совместно с границей раздела, а первая среда не движется, тогда
, 
.
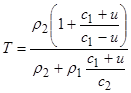Коэффициент отражения 
, при скорости движения границы равной
.
4) Если первая среда движется совместно с границей раздела 
, вторая среда не движется 
:
, 
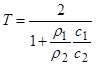
Коэффициент отражения 
, при скорости движения границы равной
.
Полученные соотношения позволяют учесть влияние движений, как границ раздела сред, так и самих сред на частоты отраженных и прошедших во вторую среду волн, а также на коэффициенты отражения и прохождения. Найдены условия отсутствия отражения, обеспечиваемые подбором скоростей движения границы раздела и самих сред.
Заключение
При взаимодействии волн с движущейся границей раздела сред движение сред существенно меняет частоты отраженной и прошедшей волн, коэффициенты отражения и прохождения. Это проявляется наиболее существенно в том случае, когда эти скорости сопоставимы по числовому значению. Подбором скорости движения границы раздела сред и скоростей сред можно добиться отсутствия отраженного сигнала. Получены обобщенные формулы преобразования частоты отраженного и частоты прошедшего сигнала, обобщенные формулы для расчета коэффициентов отражения и прохождения движущейся границы раздела с учетом подвижности сред.
Рецензенты:
Арефьев А.С., д.ф.-м.н., профессор кафедры электродинамики и антенн, Поволжский государственный университет телекоммуникаций и информатики, г.Самара.
Тяжев А.И., д.т.н., профессор, профессор кафедры Радиосвязи, радиовещания и телевидения, Поволжский государственный университет телекоммуникаций и информатики, г.Самара.