Введение
В настоящее время интерес к применению композитной арматуры в качестве рабочего армирования бетонных конструкций заметно возрос, что характеризуется увеличением научных и научно-практических публикаций, посвященных исследованию свойств и использованию композитных материалов в строительстве [1,2,6]. За последние годы эти материалы нашли применение и в России. Существующие нормы и правил проектирования бетонных конструкций с композиционными материалами находятся в стадии формирования, которые являются препятствием широкого внедрения указанной технологии в инженерную практику [4].
Таким образом, исследование напряженно-деформированного состояния (НДС) бетонных элементов, армированных композитной арматурой, является одним из этапов совершенствования метода расчета вышеуказанных конструктивных элементов. Данная проблема не может быть решена без использования современных вычислительных комплексов. Наиболее зарекомендованными программными комплексами, отображающими НДС близко к фактической работе конструкции, являются ANSYS, Lira, SCADOffice [3]. В настоящей работе предложены результаты численного исследования бетонных балок с комбинированным армированием, выполненных с использованием расчетного комплекса Lira 9.6 R9.
Цель и методика численного исследования
Целью работы является определение НДС неразрезных бетонных балок с комбинированным армированием. Комбинированное армирование – двойное армирование бетонных элементов, у которых нижняя арматура выполнена из мягких арматурных сталей, верхнее армирование – из композитной арматуры. В исследовании рассматривается поведение 3-х серий двухпролетных бетонных балок при действии сосредоточенной нагрузки. Геометрические параметры балки и схема нагружения приведены на рисунке 1.
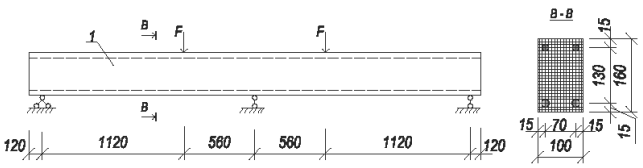
Рисунок 1. Геометрические параметры и схема нагружения исследуемых балок
Геометрические характеристики балок: пролет по 1.67 м; размеры поперечного сечения 100 × 160(h) мм. Для изготовления балок использован бетон класса В25. Нижнее армирование всех серий выполнено из 2Ø10 мм класса А400. Верхнее армирование выполнено из базальтопластиковой арматуры (Rs = 1300 МПа): первая серия 2Ø6 мм; вторая 2Ø8 мм и третья 2Ø10 мм.
Моделирование НДС балок выполнено на основе программы Lira 9.6 с учетом объемного (трехосного) напряженного состояния. Бетон балки представлен объемными конечными элементами типа жесткости 236. Этот конечный элемент предназначен для прочностного расчета континуальных объектов с учетом физической нелинейности материала. При моделировании металлической и базальтопластиковой арматуры был принят конечный элемент типа жесткости 210. Этот конечный элемент обеспечивает расчет всех видов стержневых систем с учетом физической нелинейности материала и является аналогом универсального линейного стержневого конечного элемента (тип КЭ 10).
Общий вид модели бетонных балок приведен на рисунке 2.
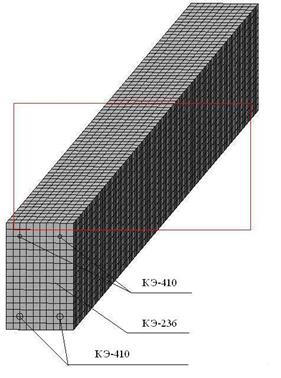
Рисунок 2. Модель исследуемых балок
Предварительные расчеты балок показали, что разрушение элементов произойдет вследствие достижения напряжений в нижней (пролетной) растянутой арматуре предела текучести. На основании этого возможность разрушения балок по бетону сжатой зоны не рассматривалась. Диаграмма «σb – εb» для бетона принята трехлинейной в соответствии с рекомендациями [5].
Обсуждение
По результатам численного моделирования получены деформированные схемы балок и схемы расположения трещин при различных стадиях нагружения. Получены графики зависимости прогиба балок от нагрузки, напряжения в арматурных стрежнях и график распределения напряжений по высоте сечения балок.
Моделированием установлена разрушающая нагрузка, которая составляет для балок первой серии 13.2 тс, для второй 13.6 тс, для третьей серии составляет 14.6 тс, т.е. с увеличением диаметра верхнего армирования прочность балок возрастает.
На рисунке 3 приведен график зависимости прогиба балок от приложенных сосредоточенных сил. Следует отметить, что за прогиб балки принимается перемещение узла, расположенного в точке приложения сосредоточенных сил. При разрушающей нагрузке, при которой жесткость балок практически равна нулю, установлены значения прогибов, которые вдвое превышают прогибы, полученные расчетом при упругой работе материалов, и соответствуют: для первой серии 11.2 мм; для второй – 8.3 мм и для третьей – 3.86 мм.
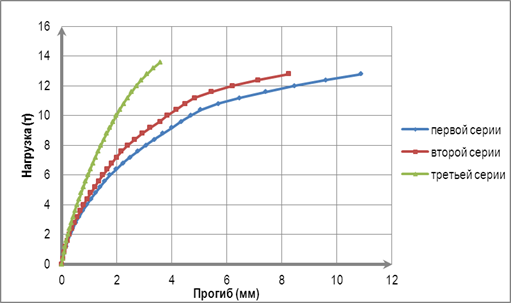
Рисунок 3. Зависимости прогиба балки от приложенной нагрузки
На рисунке 4 и 5 приведены зависимости напряжений в растянутых и сжатых арматурных стержнях от приложенной нагрузки. В соответствии с данным графиком можно выделить три характерных участка для растягивающих арматур:
1-й участок, соответствующий работе элемента без трещин, т.е. с момента загружения до момента образования трещин в растянутых зонах бетона при нагрузке 0,8 тс;
2-й участок, с момента появления трещин до момента, когда в растянутой арматуре пролетных сечений начинают нарастать неупругие деформации;
3-й участок, соответствующий пластической работе пролетной арматуры.
В соответствии с данным графиком можно определить точку его резкого перегиба с уменьшением жесткости балки практически до нуля. Данная точка соответствует нагрузке на балку в момент образования пластического шарнира в пролетных сечениях. В указанный момент напряжения в мягкой арматурной стали, расположенной в нижней зоне пролетного сечения, достигают 410…430 МПа. При этом напряжения в растянутой базальтопластиковой арматуре (опорное сечение) находятся в пределах 500…750 МПа. Отношение напряжений в базальтопластиковой арматуре в опорном сечении к напряжениям стальной арматуры в пролетах составляет 1,22…1.74. Значения нагрузки, при которой образуется пластический шарнир в пролетном сечении: для первой серии значение составляет 10.4 тс; для второй – 11.2 тс; для третьей серии разрушение произошло по сжатой зоне бетона.
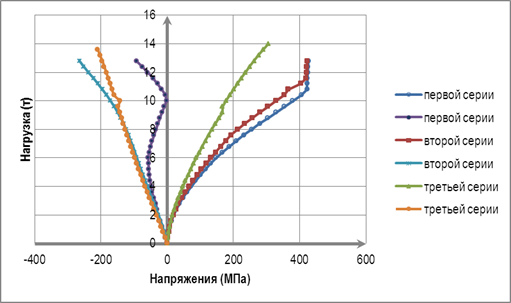
Рисунок 5. Зависимости напряжений в растянутой и сжатой арматуре от нагрузки для пролетного сечения
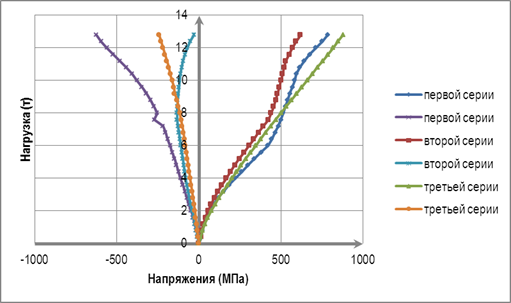
Рисунок 4. Зависимости напряжений в растянутой и сжатой арматуре от нагрузки для опорного сечения
На рисунке 5 и 6 приведена диаграмма распределения напряжений в бетоне по высоте сечения балок при разрушающей нагрузке. Напряжения в наиболее сжатых волокнах бетона при разрушении достигают: в пролетных сечениях в бетоне 20…28 МПа; в опорном сечении 23…32 МПа. Бетон растянутой зоны не работает, т.е. напряжения в бетоне соответствуют его прочности на растяжение (погрешность моделирования).
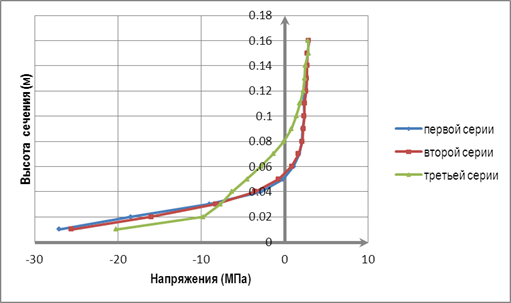
Рисунок 5. Распределения напряжений по высоте сечения балки при разрушающей нагрузке в пролетном сечении
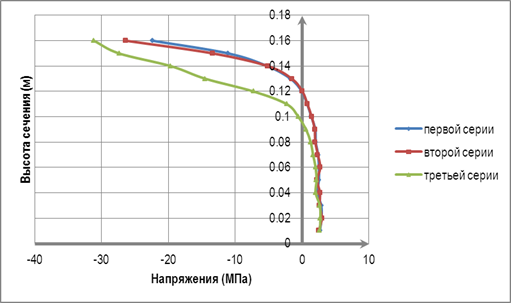
Рисунок 6. Распределения напряжений по высоте сечения балки при разрушающей нагрузке в опорном сечении
Высота сжатой зоны: в пролетных сечениях составляет для первой серии 8 см, для второй и третьей серии 5 см; в опорном сечении для первой и второй серии 6 см, для третьей – 8 см. Причем, указанные графики указывают нелинейную работу бетона, что соответствует реальной работе бетона сжатых зон изгибаемых элементов.
На рисунке 7 показан момент образования трещин в пролетных и опорном сечениях балки. Первые трещины в конечных элементах появились в опорном сечении при нагрузке 0,8–1,2 тс, при нагрузки 1,2 – 1,6 тс появились трещины в пролетных сечениях.
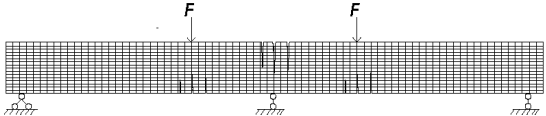
Рисунок 7. Схема расположения первых трещин при нагрузке
Выводы
1. Результаты моделирования напряженно-деформированного состояния двухпролетных неразрезных бетонных балок с комбинированным армированием с учетом нелинейных диаграмм деформирования материалов (бетона, композитной и стальной арматуры) сопоставимы с теоретическими данными, определенными по действующим нормам проектирования [2], отклонения по всем качественным показателями не превышают 12.5 %.
2. Схема расположения трещин, полученная по результатам моделирования балок по программе Lira 9.6, соответствует реальной геометрической схеме расположения трещин.
3. Моделирование балок показало возможность перераспределения усилий между опорным и пролетными сечениями, т.е. использование композитной арматуры в качестве верхнего рабочего армирования в неразрезных бетонных балках является перспективным и экономичным вариантом армирования балочных междуэтажных перекрытий зданий и сооружений.
Рецензенты:
Салихов М.Г., д.т.н., профессор, зав. кафедрой АД, Поволжский государственный технологический университет, г. Йошкар-Ола.
Низомов Д., д.т.н., профессор, заведующий лабораторией «Теория сейсмостойкости и моделирования» Института геологии, сейсмологии и сейсмостойкого строительства при академии наук Республики Таджикистан, г. Душанбе.



