Введение
Возможность эффективной эксплуатации отдельных элементов современных технических систем требует разработки новых алгоритмов управления напряжённо-деформированным состоянием. Одной из актуальных проблем в данном направлении является создание методики независимого управления напряжениями в системах с неупругими деформациями. При этом под независимым управлением напряжениями подразумевается создание в системе заданного поля напряжений с сохранением её деформированного состояния. Достижение цели в такой задаче осуществляется за счёт возможности создания в рассматриваемом теле неупругих деформаций, в качестве которых могут выступать деформации фазовых переходов, температурные деформации, пьезоэлектрические, ростовые и т.д.
В работе [5] представлен алгоритм независимого управления напряжениями, основанный на использовании теоремы о декомпозиции собственной деформации [7], которая утверждает, что любую собственную деформацию, существующую в теле, можно разложить на две составляющие: свободную от напряжений и свободную от полных деформаций. Теорема о декомпозиции, в свою очередь, является продолжением исследований о разложении гильбертовых пространств в задачах механики [3, 4, 9].
В представленной работе приведена демонстрация методики независимого управления напряжениями, где в качестве решения модельной задачи, приближённой к реальной технической проблеме, рассматривается вопрос понижения уровня механических напряжений во вращающемся диске с неравномерным по радиусу распределением температурного поля. Подобная задача может быть актуальной, например, при проектировании диска авиационной турбины.
Постановка задачи
Однородный диск постоянной толщины с радиусом 
, выполненный из изотропного материала с эффектом памяти формы, имеет отверстие радиуса 
. В процессе эксплуатации диск вращается с постоянной угловой скоростью 
, при воздействии стационарного неоднородного температурного поля, вызванного перепадом температур 
между внутренним и внешним контурами диска (рис. 1).
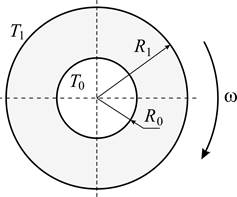
Рис. 1. Вращающийся диск под воздействием неоднородного температурного поля.
В целях повышения рабочих характеристик при помощи собственных деформаций требуется создать такие преднапряжения в диске, которые, во-первых, позволили бы максимально снизить уровень эксплуатационных термоупругих напряжений и, во-вторых, не оказывали бы влияния на первоначальные размеры диска.Рассматриваемую задачу можно разбить на три части:
1) задача определения «рабочих» напряжений 
в диске;
2) поиск оптимального поля собственных напряжений 
, необходимого для требуемого снижения напряжений ;
3) создание в диске собственных деформаций, свободных от полных деформаций, которые, с учётом технологических ограничений, соответствуют напряжениям .
1. Решение первой части производится в рамках теории термоупругости. В полярных координатах при условии осесимметричного плоско-напряжённого состояния, распределения компонент тензора напряжений будет иметь вид [10]:
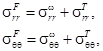(1)
где
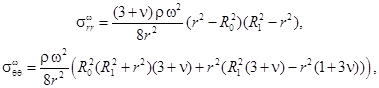(2)
вклад напряжений, вызванных центробежными силами инерции.
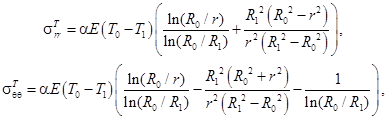(3)
температурные напряжения (рис. 2а).
2. Необходимые собственные напряжения можно найти, исходя из следующих соображений.
С учётом собственных напряжений, суммарные радиальные и окружные напряжения в диске будут складываться из составляющих от центробежных сил при неоднородном нагреве и от собственных напряжений:
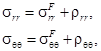(4)
где 
, 
– собственные напряжения. Эти напряжения могут быть представлены с помощью следующей функции напряжений Эйри 
:
. (5)
Вид функции подбирается в соответствии с граничными условиями для , :
, 
, (6)
где 
– произвольная гладкая функция с непрерывной производной на отрезке 
.
Представим функцию в виде следующего разложения:
. (7)
Тогда соотношения (5) перепишутся:
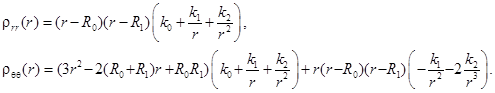(8)
Перепишем напряжения (4) в виде следующих зависимостей:
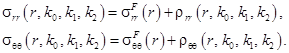(9)
Таким образом, для получения окончательной формы компонент , и 
, 
требуется определить коэффициенты 
, 
, 
.
Как уже упоминалось выше, собственные напряжения в диске должны максимально понижать уровень эксплуатационных напряжений, т.е. необходимо решить следующую задачу минимизации:
, (10)
Решение (10) позволит определить коэффициенты 
, соответствующие оптимальному полю собственных напряжений , вычисляемых по формуле (8).
3. После определения собственных напряжений необходимо перейти к алгоритму решения задачи о независимом управлении напряжениями. Данная методика предполагает учёт природы собственной деформации создаваемой в диске, а также технологических ограничений, имеющих место в процессе реализации этих деформаций.
Реально существующая собственная деформация должна быть записана в форме выражения:
. (11)
Определение элементов 
будет производиться позже.
Согласно теореме о декомпозиции, необходимая для создания напряжений собственная деформация, свободная от полных деформаций, имеет вид [7]
. (12)
Тогда задача независимого управления напряжениями сводится к поиску минимума следующего функционала:
, при условии 
. (13)
Решение
Как уже отмечалось ранее, диск должен быть выполнен из материала с эффектом памяти формы. Таким эффектом обладает, например, сплав никелида титана (TiNi, нитинол), для одной из разновидностей которого в работе [6] (Ti – 49.16%,
Ni – 49.75%) приведены следующие физико-механические свойства:
- плотность материала
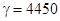кг/м3, - модуль упругости
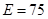ГПа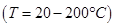 
, - коэффициент Пуассона
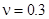, - коэффициент температурного расширения
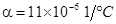, - предел текучести
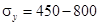МПа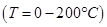 
, 
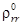температурный интервал прямого мартенситного перехода:
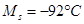(в начале),
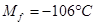(в конце), 
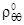температурный интервал обратного мартенситного перехода:
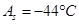(в начале),
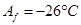(в конце).
- радиус диска
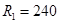мм, - радиус отверстия
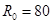мм, - температура на внешней поверхности диска
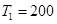
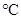, - температура на внутренней поверхности диска
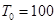
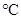, - частота вращения диска
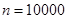об/мин.
Численное решение (10) методом Нелдера-Мида определяет оптимальные значения искомых коэффициентов:
Па/м2, 
Па/м, 
Па.
Соответствующее этим значениям распределение оптимальных собственных напряжений, а также поле суммарных напряжений в диске приведены на рис. 2. При этом поле деформаций фазовых переходов, соответствующее собственным напряжениям 
, вычисляется по формуле (12).
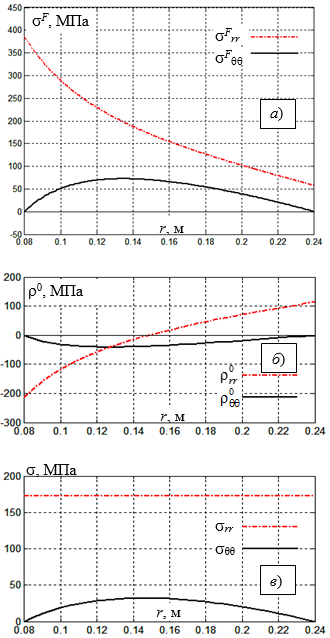
Рис. 2. Распределение эксплуатационных (a), остаточных (б) и суммарных (в) напряжений.
В современной литературе существует достаточно большое количество математических моделей, описывающих эффект памяти формы. Среди них одной из наиболее простых и в то же время хорошо согласующихся с экспериментальными данными является модель, описанная Мовчаном в работе [1].
Пусть деформации, вызванные эффектом памяти формы, реализуются за счёт поверхностных давлений 
и 
, приложенных к внутреннему и внешнему контурам диска соответственно. Такие деформации исследованы в работе [2] и определяются следующими выражениями:
, 
, (14)
где 
и 
– компоненты девиатора тензора напряжений
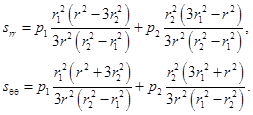(15)
Однако деформации (14) оказываются свободными от напряжений, что, вообще говоря, нежелательно, согласно условию задачи.
Одним из решений данной проблемы является создание составного диска, в каждой из частей которого за счёт поверхностного давления реализуется эффект памяти формы. Под воздействием этого нагружения элементы охлаждаются до температуры более низкой, чем конечная температура прямого мартенситного перехода [1]. При этом в составных частях накапливаются собственные (фазовые) деформации. После снятия нагрузки упругие деформации становятся равными нулю, и элементы вставляются друг в друга без натяга. При нагревании составного диска до температуры более высокой, чем конечная температура обратного мартенситного перехода, существующие собственные деформации исчезают, следовательно, составные части будут стремиться к восстановлению первоначальных размеров, что в свою очередь приведёт к появлению собственных напряжений.
С учётом формул (14) и (15) деформации фазовых переходов для составных частей диска можно выразить следующим образом:
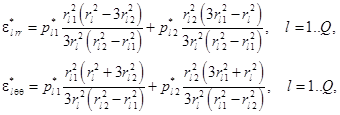(16)
где Q – количество составных элементов, 
- радиальная координата составного элемента с номером l, 
, 
- внутренний и внешний радиусы этого элемента 
,
, 
, 
,
- давление на внутреннюю поверхность элемента с номером l, 
- давление на внешнюю поверхность того же элемента 
.
В системе существует 
подобластей, в которых могут быть созданы независимые друг от друга собственные деформации, тогда согласно формуле (11)
, (17)
где 
- собственные деформации в соответствующей подобласти. Тензор можно представить в виде вектора-столбца, поскольку в данной задаче ненулевыми являются лишь две его компоненты (индекс «Т» означает транспонирование):
, . (18)
Из соотношений (16) видно, что величинами собственных деформаций можно управлять посредством изменения давлений 
и 
, которые входят в параметры 
и 
соответственно. Таким образом, в каждой подобласти существует два независимых параметра управления. Введём следующее обозначение:
Элементы 
с нечётным номером k соответствуют внутреннему давлению, элементы c чётным номером – внешнему давлению.
В связи с этим выражение (17) можно переписать следующим образом
, (4.40)
где согласно (16) и (18)
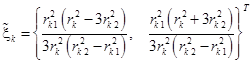и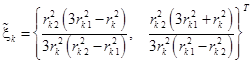 
,
На рис. 3. представлены распределения собственных напряжений для диска, состоящего из двадцати равных по толщине составных элементов. Собственные напряжения, получаемые в результате вычислений (o – радиальные напряжения, Δ – окружные), практически полностью совпадают с распределением (рис. 2б). Однако использование большого количества составных частей несёт в себе существенный недостаток, заключающийся в сложности изготовления таких дисков.
s, МПа
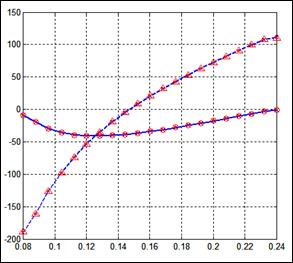r, м
Рис. 3. Распределение собственных напряжений.
Заключение
Теорема о декомпозиции собственной деформации открывает возможность независимого управления напряжениями, что является актуальным для некоторых прикладных задач. В данной работе приведён пример использования алгоритма независимого управления напряжениями в задаче понижения эксплуатационных нагрузок вращающегося диска, находящегося под действием неоднородного поля температур. В рамках представленной проблемы показаны возможности достижения требуемого поля напряжений при условии отсутствия полных деформаций.
Работа выполнена при финансовой поддержке РФФИ (проект № 12-01-31404_мол_а).
Рецензенты:
Акулич Ю.В., д.ф.-м.н., профессор кафедры теоретической механики, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Пермский национальный исследовательский политехнический университет», г. Пермь.
Кротов Л.Н., д.ф.-м.н., доцент, зав. кафедрой прикладной физики, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Пермский национальный исследовательский политехнический университет», г. Пермь.