Введение
В настоящее время основным путём улучшения характеристик цифровых электронных устройств является технологический путь развития. Данный путь предусматривает постоянное улучшение технологии производства полупроводниковой электронной компонентной базы, и такая тенденция была замечена на самом раннем этапе развития микроэлектроники — в 1965 году один из основателей фирмы Intel Гордон Мур высказал предположение, что число транзисторов на кристалле будет удваиваться каждые 24 месяца, а если такая тенденция продолжится, то мощность вычислительных устройств экспоненциально возрастёт на протяжении относительно короткого промежутка времени [6]. В соответствии с законом Мура массовая микроэлектроника, а вслед за ней и вычислительная техника, развиваются до настоящего времени.
Однако, кроме экстенсивного развития, существуют альтернативные способы повышения производительности цифровой электронной техники. Одним из таких способов является частичный или полный отказ от повсеместно распространённого использования:
- двоичной позиционной системы для представления данных и программ;
- двоичной логики для управления вычислительным процессом.
Одной из альтернатив является использование:
- многозначной системы счисления для представления чисел;
- многозначной (или многоуровневой) (с числом состояний больше двух) или нечёткой логики (с представлением логической величины в виде дробного числа на отрезке [0, 1]).
Частным случаем применения многоуровневой системы в элементной базе цифровой электроники является применение троичной симметричной системы с отрицательным (1), нулевым (0) и положительным (1) логическими уровнями. Такая система применялась практически в ЭВМ «Сетунь», в качестве обоснования выбора выдвинуты следующие аргументы [2]:
- Экономность (при представлении одного и того же числа троичная симметричная система счисления на 59% экономнее десятичной и на 5,4% экономнее двоичного; для представления чисел с одинаковой точностью нужно в 2,10 раза больше троичных цифр, чем десятичных, и в 1,58 раза меньше, чем двоичных). Это ускоряет последовательную передачу и обработку данных.
- Естественность представления отрицательных чисел (при операциях нет необходимости вводить дополнительный и обратный коды, как с двоичной системой; знак числа определяется знаком старшей значащей цифры; для изменения знака числа требуется инвертировать знаки всех цифр числа).
- Отсутствие проблемы округления (операция округления соответствует простому усечению разрядов числа).
Данные преимущества могут привести к упрощению структурных схем вычислительных и логических узлов ЭВМ.
Классификация
Элементарные узлы цифровой электронной компонентной базы — логические элементы — могут быть выполнены с использованием различных схемотехнических подходов. Рассмотрим такие подходы для известных автору трёхуровневых элементов, работающих в симметричной троичной системе и реализуемых по стандартной КМОП-технологии интегральных микросхем.
В качестве основы для выявления подходов создания электронных логических элементов возьмём следующие положения.
- В качестве физической величины для представления логических уровней может быть напряжение или ток.
- Сигнал между элементами может передаваться по одному или нескольким проводам. При передаче по нескольким проводам возможно уменьшение числа логических уровней на каждом проводе.
Кроме того, логические элементы могут иметь схемотехнические особенности.
Наиболее очевидными являются логические элементы с применением делителей напряжения, в которых третий (промежуточный) логический уровень обеспечивается делением напряжения питания (рисунок 1а).
Оригинальны логические элементы с представлением логических значений уровнями тока (рисунок 1б). Достоинство таких схем — реализация операции логического сложения монтажным способом, то есть соединением проводов; таким образом, возможно увеличение степени интеграции и снижение энергопотребления, как это сделано в 32-битном умножителе, работающем со знакопозиционным четверичным кодом [3]. Троичные устройства на данном принципе предложены автором настоящей статьи.
Логические элементы с промежуточным биполярным кодированием (рисунок 1в) можно считать промежуточными между однопроводными и двухпроводными. Хотя на вход такого элемента сигнал поступает по одному проводу, после прохождения входного каскада он расщепляется на две составляющих A и B, которые затем объединяются на выходе [5].
Схемы с расщеплёнными входами и выходами (рисунок 2а) основаны на использовании всего двух блоков транзисторов, к каждому из которых подключаются компоненты входов.
Другой тип логических элементов — с двоичным двухпроводным кодированием — представляет собой комбинационную логическую схему, принимающую двоично-кодированный сигнал на входах и выдающую подобный сигнал на выход (рисунок 2б). На данный тип похож элемент с трёхпроводным кодированием, в котором для представления троичного кода используется «единичная» система счисления (рисунок 2в).
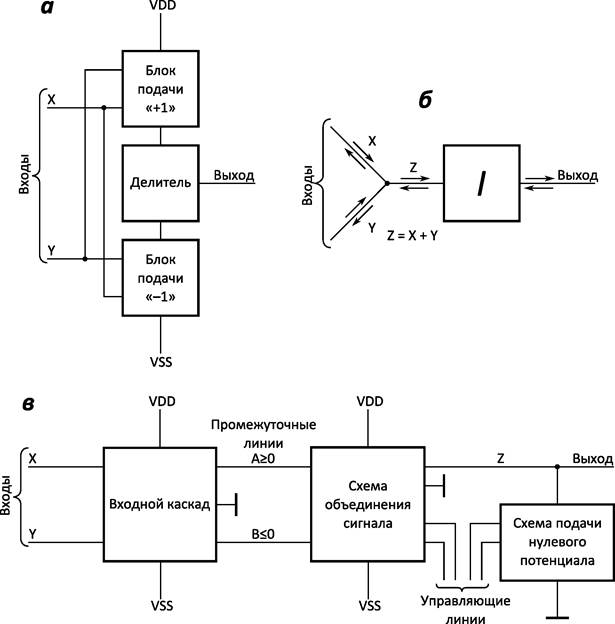
Рисунок 1 — Обобщённые блок-схемы трёхуровневых логических элементов с однопроводной передачей сигналов: а — с применением делителей напряжения, б — с токовым кодированием; в — с промежуточным биполярным кодированием
На основе известных нам сведений построим диаграмму (рисунок 3).
Все рассмотренные типы логических элементов, кроме элементов с токовым кодированием, используют различные уровни напряжений для представления различных логических уровней (потенциальное кодирование). Кроме потенциального и токового кодирования логических значений, возможны другие способы, например фазовое, частотное, зарядовое, квантовое. Однако автору неизвестны практические разработки трёхуровневых логических элементов, созданных с применением таких видов кодирования на базе КМОП-технологии.
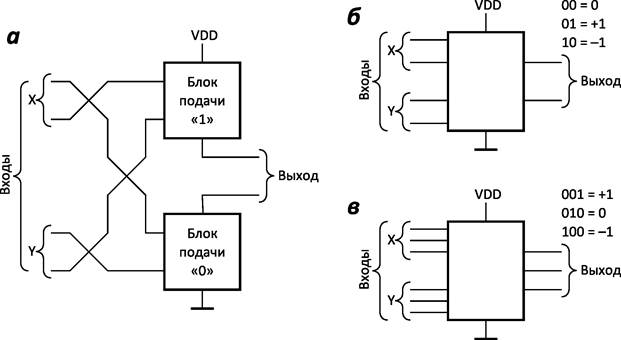
Рисунок 2 — Обобщённые блок-схемы трёхуровневых логических элементов с многопроводной передачей сигналов: а — с расщеплёнными входами и выходами;
б — с двоичным двухпроводным кодированием;
в — с трёхпроводным (единичным) кодированием
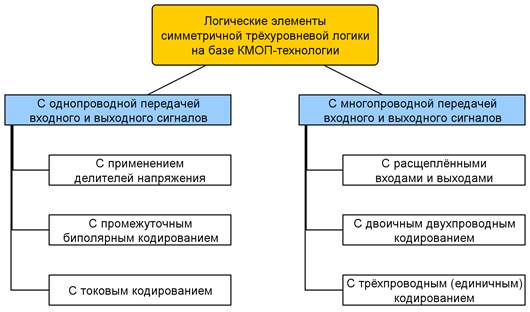
Рисунок 3 — Классификация логических элементов симметричной трёхуровневой логики на базе КМОП-технологии
Методика сравнения
Сравнение трёхуровневых логических элементов, спроектированных с использованием различных подходов, наиболее интересно при рассмотрении их динамических параметров. Для измерения этих параметров существуют методы, описанные в государственном стандарте [1]. Однако данный стандарт распространяется на двоичные цифровые микросхемы, поэтому для измерения параметров трёхуровневых цифровых микросхем необходима новая методика, опирающаяся на стандарт.
Принципиально важным является то, что в отличие от двоичных схем, где уровень сигнала может изменяться лишь в двух направлениях: от нуля к единице и от единицы до нуля, в троичных схемах возможно изменение уровня сигнала по четырём направлениям между соседними уровнями и по двум — между противоположными.
Отсюда получается большое количество возможных измеряемых параметров (рисунок 4).
Помимо этого, для двоичных КМОП-схем уровнями отсчёта принимают уровни 10, 50 и 90% от напряжения питания [4]. В случае троичных логических элементов имеет смысл установить такие уровни отдельно для интервалов напряжений в положительном и отрицательном направлениях, так как в некоторых типах логических элементов применяется источник питания со средней точкой.
Характеристики схем с многопроводным кодированием можно измерять по методике для двоичных схем, однако в этом случае временем задержки следует считать наиболее длинный промежуток времени между самым ранним изменением сигнала на одном из проводов входа и самым поздним откликом на одном из проводов выхода.
Заключение
Исходя из принципов работы рассмотренных логических элементов, можно дать рекомендации по использованию конкретных типов элементов для конструирования устройств.
1. Логические элементы с делителями потребляют ток в статическом режиме и работают медленнее двоичных логических элементов и могут быть применены лишь к схемам, некритичным к энергопотреблению либо скорости работы.
2. Логические элементы с промежуточным биполярным кодированием при отсутствии тока потребления в статическом режиме являются наиболее универсальными, но они наиболее громоздкие из всех рассмотренных схем.
3. Логические элементы с расщеплёнными входами экономны с точки зрения использования транзисторов, и они также могут быть широко использованы.
4. Логические элементы с двоичным кодированием троичного сигнала могут быть реализованы на основе существующих двоичных программируемых логических интегральных схем (ПЛИС), что даёт возможность быстрого проектирования троичных схем. Очевидный недостаток — избыточность по числу компонентов.
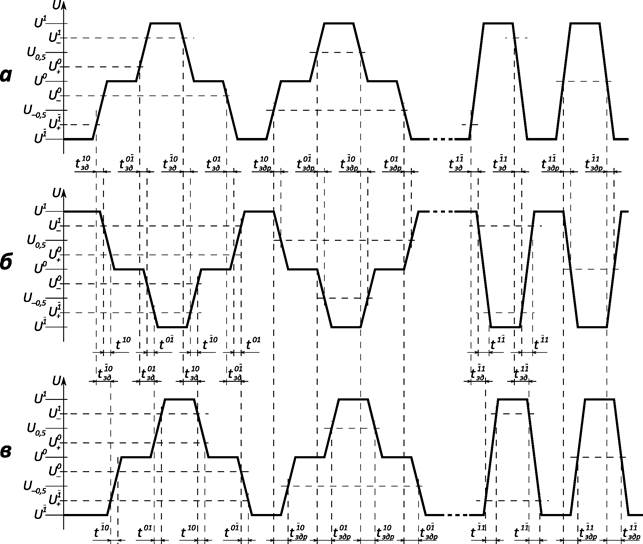
Рисунок 4 — Иллюстрация методики измерения и сравнения динамических параметров трёхуровневых логических элементов: а — напряжение на входе; б — напряжение на инвертирующем выходе; в — напряжение на неинвертирующем выходе; U1, U0, U1 — логические уровни; U–1, U+0, U0,U–0, U+1 — уровни отсчёта (U0 является одновременно и логическим уровнем, и уровнем отсчёта); tAB — времена перехода из состояния A в состояние B; tздAB — времена задержки включения и выключения;
tздрAB — времена задержки распространения
5. Логические элементы с трёхпроводным единичным кодированием могут быть интересны своей потенциальной надёжностью в представлении данных и простой (монтажной) реализацией инвертора. Однако их применение в больших интегральных схемах может оказаться проблематичным из-за необходимости разводить три линии проводников между каждой парой соединённых элементов.
6. Логические элементы с токовым кодированием интересны для создания динамических узлов цифровой техники (сумматоров, умножителей, арифметико-логических устройств и др.), так как за счёт эффекта монтажного сложения возможна значительная экономия места на полупроводниковой подложке, а за счёт токового кодирования может быть достигнута высокая скорость работы и надёжность передачи данных. При этом данные узлы должны быть постоянно нагружены задачами и работать на предельной тактовой частоте либо снабжены схемами управления питанием для их отключения в случае бездействия.
Сравнение различных типов троичных логических элементов возможно путём измерения динамических характеристик по описанной в данной статье методике.
Работа выполнена при поддержке РФФИ в рамках научного проекта № 12-07-31184 мол_а.
Рецензенты:
Мурашев В.Н., д. т. н., профессор кафедры полупроводниковой электроники и физики полупроводников, НИТУ «МИСиС», г. Москва.
Кольцов Г.И., д. ф.-м. н., профессор кафедры полупроводниковой электроники и физики полупроводников, НИТУ «МИСиС», г. Москва.



