Введение
Известно, что математические модели ряда физических процессов диффузии и теплопроводности основаны на уравнении параболического типа второго порядка:
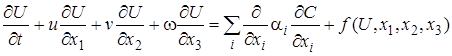, (1)
где U – некоторый физический параметр (при рассмотрении задачи переноса примесей загрязняющего вещества в атмосфере U обозначает концентрацию; при рассмотрении задачи теплопроводности U обозначает температуру), t – время, 
– средние скорости переноса вдоль осей координат x, y, z соответственно, αi – вектор коэффициентов нелинейного переноса вдоль осей координат (i = 1,2,3).
В случае произвольных граничных условий уравнение (1) не решается аналитически, поэтому для прикладных задач используют различные численные методы [1; 4]. Наиболее известными из них являются метод конечных элементов, метод конечных разностей, разрывный метод Галеркина [8; 9]. В их основе лежит аппроксимация производных конечно–разностными уравнениями: на непрерывное поле пространства накладывается равномерная сетка, и решение ищется в узлах этой сетки. После составления конечно–разностного уравнения необходимо провести анализ устойчивости и сходимости полученного решения к поставленной дифференциальной задаче. Различают следующие типы разностных схем: явные, неявные, полунеявные, компактные, консервативные, схемы на смещенных сетках. Для любых типов разностных схем необходимо доказать, что полученное с помощью них разностное уравнение устойчиво и сходится к решению поставленной задачи. Ряд экспериментальных данных, в частности неоднородность распределения поверхностного загрязнения, не объясняется существующими математическими моделями распространения загрязнений [6], основанных на решении уравнения (1).
Модели клеточных автоматов
Часто основные особенности сложной динамической системы, состоящей из большого количества элементов, нелинейно взаимодействующих друг с другом, могут быть выражены рядом простых правил. Такие системы традиционно описывают в рамках вероятностных клеточных автоматов (КА) [7]. Клеточные автоматы нашли устойчивое применение в качестве концептуальных и практических моделей (модели уравнения теплопроводности, волнового уравнения [9], уравнения Навье – Стокса [10], модели диффузии [2; 7] и др.).
Клеточные автоматы являются дискретными динамическими системами. КА использует множество переменных, которые взаимодействуют только локально и единообразно и относятся к моделям, явным образом сводящим макроскопические явления к точно определенным микроскопическим процессам. В соответствии с парадигмой КА, моделирование производится на n-мерной дискретной сетке, каждая ячейка представляет собой часть моделируемого физического пространства и описывается набором безразмерных характеристик. Временная ось разбита на равные промежутки времени – итерации. Единицей длины является клетка, а единицей времени – один итерационный цикл. Состояние каждого элемента сетки в методе КА изменяется последовательно шаг за шагом в соответствии с некоторыми локально определенными правилами перехода. Управляющие правила перехода записываются в виде:
, (2)
где 
и 
– два последовательных во времени значения состояния клетки; 
– некоторое множество клеток, соседних с клеткой 
называемое окрестностью; 
- правило клеточного автомата, по которому определяется новое значение определенного параметра клетки. Смена состояния клетки происходит с учетом ее предыдущего состояния и состояний клеток окрестности с заданной вероятностью. Результатом моделирования является матрица состояний клеточного автомата, при решении задачи диффузии матрица состояний хранит безразмерные значения концентраций, в случае решении задачи теплопроводности матрица состояний хранит безразмерное значение температуры. Аналогом матрицы состояний можно считать сеточную функцию, получаемую при решении методом конечных разностей ДУ в частных производных.
Таким образом, поведение КА полностью определяется локальными зависимостями – так же, как и в большом классе непрерывных динамических систем, определенных уравнениями в частных производных [2; 7]. Как правило, состояние клетки представляет собой целочисленный или булев словарь, таким образом, исключается возможность накопления ошибок вычислений (присущих для ЭВМ при операциях с вещественными числами). Метод клеточных автоматов естественным образом учитывает дискретные граничные условия. Благодаря локальному взаимодействию состояний клеток алгоритм правил КА легко распараллеливается.
Математическая модель диффузионного переноса Марголуса
Авторами Тоффоли и Марголусом [7] предложена математическая модель диффузионного переноса в рамках вычислительной среды двумерных клеточных автоматов.
Двумерный клеточный автомат представляет собой двумерную сетку, каждая клетка которой характеризует некоторую область пространства. Каждый элемент клетки находится в одном из двух состояний {0} – отсутствие вещества и {1} – заполнено веществом. Клетки в одинаковом состоянии никак друг от друга не отличаются. Сетка разделена на окрестности (рис. 1), с помощью управляющего правила диффузии (3) происходит изменение состояния клеток всего клеточного автомата согласно общему правилу (2).
X0={(i,j):i mod 2=0 & j mod 2=0}
X1={(i,j):i mod 2=1 & j mod 2=1}
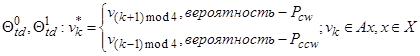(3)
где 
– состояние клетки k в момент времени t+1, vk – состояние клетки k в момент времени t, X0 – четное подмножество блоков разбиения, X1 – нечетное подмножество блоков. Для получения остатка от деления используется операция mod. Шаблон T локальной окрестности L (окрестность Марголуса) задается выражением:
T={(i,j),(i+1,j),(i+1,j+1),(i,j+1)}
L(i,j)={(v0, (i,j)), (v1, (i+1,j)), (v2, (i+1,j+1)), (v3, (i,j+1))} (4)
Правило (3) в математической модели диффузии работает следующим образом.
1. Матрица клеточного автомата разбивается на два подмножества X0, X1 - четное и нечетное (рис. 1).
2. Оператор Θ0td применяется ко всем клеткам четного подмножества, Θ1td применяется ко всем клеткам нечетного подмножества.
3. Каждый из операторов Θ0td и Θ1td поворачивает блоки соответствующего подмножества по часовой или против часовой стрелки с вероятностью Pcw и Pccw соответственно.
Графически действие правила диффузии (3) показано на рис. 1, и в работе [2] показан переход от дискретного представления состояния клеток автомата к континуальному, используя уравнение Смоулховского – Фокера – Планка. Таким образом, действие правила диффузии (3) соответствует действию оператора второго порядка уравнения параболического типа, другими словами, правило (3) является численным методом решения дифференциального уравнения с соответствующим оператором второго порядка.
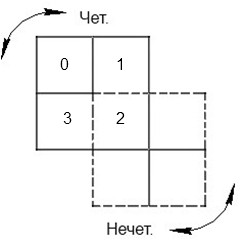
Рисунок 1. Синхронное правило диффузии двумерного клеточного автомата. Цифрами обозначена нумерация ячеек окрестности (v0,v1,v2,v3). Сплошной линией выделен блок четного разбиения, пунктирной линией – блок нечетного разбиения.
Оказалось, что описанная математическая модель Марголуса обладает локальной неизотропностью, в результате чего полученная функция распределения вероятности обнаружения частицы на некотором расстоянии от исходного местоположения имеет дискретный вид (рис. 2). Такое распределение не соответствует реальному процессу диффузии.
Численный метод решения уравнения параболического типа
Предлагается следующий численный метод решения уравнения параболического типа с оператором второго порядка для задач диффузии и теплопроводности на окрестности Марголуса, позволяющий избежать локальной неизотропности диффузии и получить непрерывную функцию распределения вероятности:
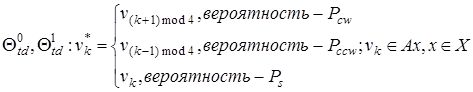(5)
где Θ0|1td и Θ0|1td – правило диффузии, верхние индексы указывают четность обрабатываемых блоков, четность выбирается равноверноятно на каждом такте одной итерации, Pcw – вероятность поворота блока по часовой стрелке, Pccw – вероятность поворота блока против часовой стрелки, Ps – вероятность того, что выбранный блок не будет поворачиваться.
Правило (5) действует следующим образом.
1. Матрица клеточного автомата разбивается на два подмножества X0, X1 - четное и нечетное (рис. 1).
2. Оператор Θ0td применяется ко всем клеткам четного подмножества, Θ1td применяется ко всем клеткам нечетного подмножества.
3. Каждый из операторов Θ0td и Θ1td поворачивает блоки соответствующего подмножества по часовой или против часовой стрелки с вероятностью Pcw и Pccw соответственно.
4. На каждом такте одной итерации оператор Θ1td или Θ1td выбирается случайно.
Сравнение среднего расчета по правилу Марголуса (3) и предложенному в работе правилу (5) приведено на рис. 2. Видно, что правило (5) обеспечивает непрерывную функцию распределения, что соответствует процессу диффузии и теплопроводности.
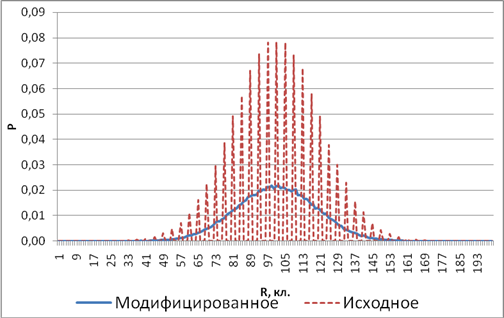
Рисунок 2. Вероятность P обнаружить частицу на расстоянии R, клеток от первоначального положения для двух правил КА: Марголуса (3) и авторского (5). Время моделирования t=100 итераций.
Математическая модель трехмерной диффузии / теплопроводности
Трехмерная математическая модель диффузии / теплопроводности на языке правил клеточных автоматов записывается следующим образом.
Трехмерный клеточный автомат представляет собой трехмерную сетку, каждая ячейка которой характеризует некоторую область пространства. Каждая ячейка находится в одном из двух состояний {0} – отсутствие вещества и {1} – заполнено веществом. Ячейки в одинаковом состоянии никак друг от друга не отличаются. Сетка разделена на окрестности блоками размера 2х2х2 ячейки. С равной вероятностью для каждого блока четного и нечетного разбиения производится вращение по часовой или против часовой стрелки вдоль координатных осей x,y,z
Θtd = PxΘx td+PyΘy td+PzΘz td
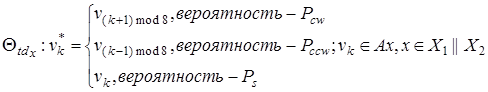
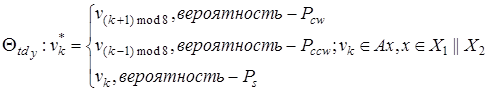
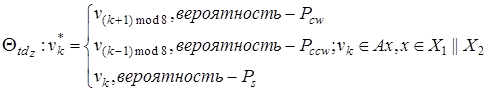(6)
где Pcw – вероятность вращения блока по часовой стрелке, Pсcw – вероятность вращения блока против часовой стрелки, Ps – вероятность не вращения блока, Px, Py, Pz – вероятность вращения вдоль осей x, y и z соответственно, Θx td, Θy td, Θz td – операторы диффузии вдоль осей x, y и z соответственно.
Рассчитан безразмерный коэффициент диффузии по математическим моделям (5, 6) в одно-, дву- и трехмерном случаях, результаты представлены в таблице 1.
Таблица 1. Значения безразмерных коэффициентов диффузии
|
Размерность пространства |
d=1 |
d=2 |
d=3 |
|
Математическая модель (3) |
1,0* |
3/2* |
23/18* |
|
Математическая модель (5, 6) |
1,0 |
4/9 |
232/972 |
* – Значения получены в работе [2]
Проведена верификация математической модели (6) путем сравнения результата с известным решением уравнения (7) с однородными граничными условиями и действием мгновенного точечного источника единичной мощности в начале координат. Dx=Dy=Dz=10-4м2/с [4]
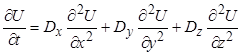(7)
Согласно расчетам относительная погрешность δ=1%
,
где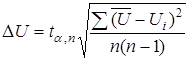 
, n = 100, – количество экспериментов, α = 0.95 – доверительная вероятность, 
– коэффициент Стьюдента.
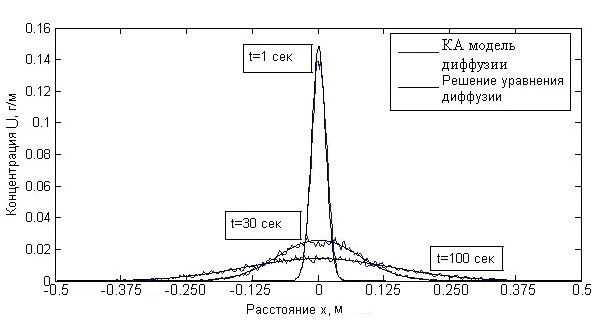
Рисунок 3. Верификация математической модели (6). Молекулярная диффузия концентрации загрязняющего вещества от мгновенного точечного источника загрязнения с координатами (0,0,0).
Заключение
Предложен численный метод решения уравнений параболического типа и описаны двумерная и трехмерная математические модели (5, 6) диффузии / теплопроводности на окрестности Марголуса, обеспечивающие непрерывную функцию распределения физического параметра. Проведена верификация математической модели трехмерной диффузии, отклонение полученного решения по математической модели (6) от известного составило порядка 1%.
Рецензенты:
Вараксин А.Н., д.ф.м.-н., профессор, заведующий лабораторией математического моделирования в экологии и медицине Федерального государственного бюджетного учреждения науки «Институт промышленной экологии Уральского отделения Российской академии наук», г. Екатеринбург.
Максимов В.И., д.ф.м.-н., профессор, заведующий отделом дифференциальных уравнений Федерального государственного бюджетного учреждения науки «Институт математики и механики им. Н.Н. Красовского Уральского отделения Российской академии наук», г.Екатеринбург.