Постановка задачи
Исследование конвективного теплообмена между высокотемпературными газовыми потоками и поверхностью обтекаемого тела сводится, в основном, к определению плотности конвективного потока. При этом используются калориметрические методы. Эти методы, как правило, применяются при реализации в процессе теплообмена регулярного режима первого рода /2/. В этой связи калориметрические датчики получили наименование калориметров регулярного режима. В экспериментальной практике применяются два вида таких неохлаждаемых калориметров - "таблеточного" и "стержневого" типов. Название типов калориметров обусловлено формой их теплоприемного элемента. В работе исследуется метод определения тепловых потоков высокой интенсивности с использованием калориметров "таблеточного" типа и анализируются условия расчета тепловых потоков по экспериментальным данным с минимальной погрешностью.
Калориметр "таблеточного" типа
Теоретической базой калориметра "таблеточного" типа является уравнение первого закона термодинамики. Его физический принцип заключается в том, что процесс конвективного теплообмена между набегающим потоком и калориметром организуется таким образом, чтобы вся теплота Q, подведенная к теплоприемному элементу калориметра известной массы и геометрической формы, затрачивалась на изменение его энтальпии, т. е. Q = ∆I и теплоотвод от датчика отсутствует. В этом случае
![]() , (1)
, (1)
где m - масса теплоприемного элемента калориметра, с - удельная теплоемкость материала теплоприемного элемента калориметра, взятая при среднемассовой температуре ![]() ,
, ![]() - время экспозиции теплового потока.
- время экспозиции теплового потока.
Выражение (1) легко преобразуется к виду, удобному для расчета плотности теплового потока, если выбрать соответствующую геометрическую форму теплоприемного элемента, например такую, чтобы расходуемая на его нагревание теплота Q была передана через известную теплоприемную поверхность элемента F. При этом важно, чтобы эта поверхность однозначно определяла объем теплоприемного элемента, т.е., чтобы в выражении (1) массу тела m можно было представить в виде:
![]() , (2)
, (2)
где ![]() - плотность материала таблетки, F - площадь поверхности, воспринимающей теплоту Q,
- плотность материала таблетки, F - площадь поверхности, воспринимающей теплоту Q, ![]() - толщина таблетки (рис. 1).
- толщина таблетки (рис. 1).
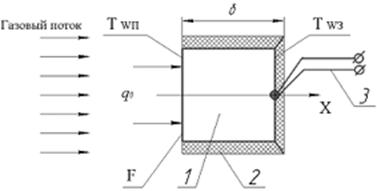
Рис. 1. Схема калориметра «таблеточного» типа
1 - теплоприемный элемент, 2- теплоизоляция, 3 - термопара, q0 - плотность теплового потока, Tw, п и Tw, - температура передней и задней поверхностей, соответственно, F - площадь поверхности, воспринимающая теплоту.
Кроме того, в (1) необходимо выполнить условие:
![]() , (3)
, (3)
где ![]() и
и ![]() - среднемассовые температуры теплоприемного элемента датчика в моменты времени
- среднемассовые температуры теплоприемного элемента датчика в моменты времени ![]() и
и ![]() .
.
Последнее возможно при условии линейной зависимости от времени среднемассовой температуры теплоприемного элемента датчика ![]() , которая рассчитывается по известной формуле:
, которая рассчитывается по известной формуле:
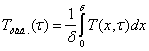 , (4)
, (4)
Эти условия, с некоторым приближением, выполняются при отсутствии теплоотвода от датчика в корпус. Тогда удельный тепловой поток определяется по уравнению:
![]() , (5)
, (5)
где ![]() - изменение температуры таблетки в течение интервала времени экспозиции
- изменение температуры таблетки в течение интервала времени экспозиции ![]() .
.
Однако в реальном эксперименте имеет место теплоотвод от датчика в корпус калориметра. В этом случае уравнение баланса для удельного теплового потока, падающего на датчик, будет иметь вид /1/:
![]() , (6)
, (6)
где Θ = T - T0 - избыточная температура датчика; T, [К] - текущее значение температуры датчика; T0, [К] - температура датчика до начала воздействия теплового потока (принимается, что она равна температуре корпуса калориметра); B = Cд/F, [Дж/м2·К] - интегральная теплоёмкость датчика на единицу рабочей площади; Сд, [Дж/град.] - интегральная теплоёмкость датчика, средняя в рабочем интервале температур; F,[м2] - площадь поверхности датчика, воспринимающей тепловой поток; К, [Вт/м2·К] - интегральный коэффициент теплопередачи от датчика в корпус; а ![]() , [с] - постоянная времени датчика.
, [с] - постоянная времени датчика.
Решение уравнения (1) имеет вид:
![]() , (7)
, (7)
где Θm = Tm - T0 - условное максимальное, асимптотическое значение Θ при τ ![]() .
.
Темп роста температуры по времени, как следует из (7), выражается уравнением:
![]() , (8)
, (8)
где τ0 - момент времени для аппроксимирующей зависимости T = f(τ), соответствующей уравнению (7), когда Θ = 0.
Как видно из уравнений (8) и (6), в начале повышения температуры датчика, когда τ0=0, величина ![]() имеет максимальную величину, соответствующую полному тепловому потоку. Однако, из-за наличия переходных процессов, температура датчика выходит на регулярный режим в течение некоторого времени τ1, как это видно из графика Θ=f(τ), представленного на рис. 2 (кривая 2).
имеет максимальную величину, соответствующую полному тепловому потоку. Однако, из-за наличия переходных процессов, температура датчика выходит на регулярный режим в течение некоторого времени τ1, как это видно из графика Θ=f(τ), представленного на рис. 2 (кривая 2).
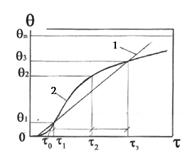
Рис. 2. Изменение температуры датчика калориметра по времени (термограмма калориметра); 1 - линейное приближение термограммы, 2 - термограмма ![]() теплоприемного элемента.
теплоприемного элемента.
Использовать для расчета можно только данные, полученные по истечении этого времени, однако, как можно заметить из уравнения (6), тепловой поток, рассчитанный по этим данным, будет заниженным.
Кроме того, поскольку в расчете теплового потока по уравнению (3) используется разность температур датчика за некоторый интервал времени, то будет иметь место значительная погрешность расчета теплового потока: при малом интервале - из-за близости величин температуры датчика в соседних расчетных точках, при большом интервале - за счет изменения ![]() за время между расчетными точками.
за время между расчетными точками.
В экспериментальной практике, в ряде задач авиационной и ракетной техники /3/ приходится сталкиваться с необходимостью определения тепловых потоков большой интенсивности (до q > 103 кВт/м2). В этом случае, с целью сохранения датчика и повышения точности калориметрирования, время экспозиции теплового потока на приемный элемент калориметра сокращается до минимума (десятые и сотые доли секунды). В результате этого регистрируется только начальная часть термограммы и отклонение от линейности изменения температуры датчика по времени (![]() =f(τ)) невелико. В этой связи, возникла необходимость разработки метода определения интенсивных тепловых потоков, сводящего к минимуму указанные инструментальные и методические погрешности. Алгоритм такого метода предложен в данной работе.
=f(τ)) невелико. В этой связи, возникла необходимость разработки метода определения интенсивных тепловых потоков, сводящего к минимуму указанные инструментальные и методические погрешности. Алгоритм такого метода предложен в данной работе.
Суть метода и алгоритм определения теплового потока
На рисунке 2 приведена типичная термограмма «таблеточного» калориметра регулярного режима. Здесь же линией 1 представлена линейная аппроксимация термограммы ![]() , которая используется для определения плотности теплового протока, согласно (3). Видно заметное различие зависимостей 1 и 2, что вызывает значительную погрешность в определении теплового потока.
, которая используется для определения плотности теплового протока, согласно (3). Видно заметное различие зависимостей 1 и 2, что вызывает значительную погрешность в определении теплового потока.
При обработке экспериментальных данных, прежде всего, определяется диапазон, в пределах которого имеет место регулярный режим, т.е. справедливо уравнение (7) и постоянная времени а = const. Поскольку а = Δτ/lnX /2/, где Δτ=const - интервал между соседними расчетными точками, то условие а = const заменяется условием X=const , где
X=(Θi - Θi-1)/(Θi+1 - Θi) (11)
и рабочий диапазон Θ = f(τ) определяется, исходя из графика Х=f(τ), построенного по всему диапазону экспериментальных точек.
Затем, определяется по (3), в первом приближении, "линейная" величина плотности теплового потока ![]() по двум точкам
по двум точкам ![]() и
и ![]() линии 1 термограммы, взятым в начале и в конце регулярного режима (рис. 2), в виде:
линии 1 термограммы, взятым в начале и в конце регулярного режима (рис. 2), в виде:
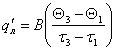 , (9)
, (9)
где ![]() . Значения Θ1 и Θ2 берутся из термограммы в точках
. Значения Θ1 и Θ2 берутся из термограммы в точках ![]() и τ3, соответственно, (см. рис.2),.
и τ3, соответственно, (см. рис.2),.
Поправку к определенной по (9) величине теплового потока представим в виде:
![]() , (10)
, (10)
где q0 - реальная величина плотности теплового потока, падающего на поверхность F, ![]() - величина теплового потока, определенная в рамках принятого линейного приближения, но с переносом первой расчетной точки в точку
- величина теплового потока, определенная в рамках принятого линейного приближения, но с переносом первой расчетной точки в точку ![]() ,= 0 (Θ1 = Θ0 = 0) (рис.2). Кривая (2), построенная по уравнению (7), аппроксимирует ход действительного процесса Θ = f(τ). Параметры этого уравнения и положение точки "0" определяется после ряда итераций.
,= 0 (Θ1 = Θ0 = 0) (рис.2). Кривая (2), построенная по уравнению (7), аппроксимирует ход действительного процесса Θ = f(τ). Параметры этого уравнения и положение точки "0" определяется после ряда итераций.
В рабочем диапазоне определяется постоянная времени а:
![]() , (12)
, (12)
где ![]() - интервал времени между соседними точками,
- интервал времени между соседними точками, ![]() средняя величина, определяемая с использованием соотношения /5/:
средняя величина, определяемая с использованием соотношения /5/:
![]() (13),
(13),
где i - текущий номер точки.
При малых ![]() , для повышения точности расчетов, необходимо усреднять значения температуры по k точкам. Условия осреднения будут описаны ниже. Тогда постоянная времени калориметра может быть определена в виде:
, для повышения точности расчетов, необходимо усреднять значения температуры по k точкам. Условия осреднения будут описаны ниже. Тогда постоянная времени калориметра может быть определена в виде:
![]() , (14)
, (14)
где ![]() = k·
= k·![]() ,
, ![]() - рассчитана по уравнению (13), а величины температур Θ взяты как средние по интервалу из k точек.
- рассчитана по уравнению (13), а величины температур Θ взяты как средние по интервалу из k точек.
Далее, используя (6), находим, в перовом приближении, расчетную величину максимальной температуры ![]() в виде:
в виде:
![]() , (15)
, (15)
где ![]() - плотность теплового потока в первом приближении (9).
- плотность теплового потока в первом приближении (9).
Затем, используя (7), находим интервал времени ![]() от точки
от точки ![]() , в которой
, в которой ![]() , до точки 1, где
, до точки 1, где ![]() (см. рис. 2):
(см. рис. 2):
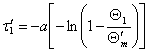 . (16)
. (16)
Принимая за начало отсчета точку ![]() = 0, запишем новое значение времени для точки 3 в виде:
= 0, запишем новое значение времени для точки 3 в виде:
![]() . (17)
. (17)
Затем определяем по уравнению (5) следующее приближение величины плотности теплового потока ![]() , используя вместо точки
, используя вместо точки ![]() точку
точку ![]() , в которой
, в которой ![]() = 0. Получаем:
= 0. Получаем:
![]() , (18)
, (18)
а также найдем, во втором приближении, расчетную величину максимальной температуры ![]() в виде:
в виде:
![]() . (19)
. (19)
Используя (6), (7) и (10), запишем, в общем виде, уравнение для определения поправки к ![]()
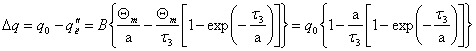 (20)
(20)
и определяем, во втором приближении, величину ![]()
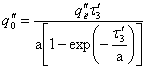 . (21)
. (21)
Затем рассчитывается следующее приближение, начиная с (15), где вместо ![]() ставится
ставится ![]() . Итерации повторяются до получения заданной сходимости.
. Итерации повторяются до получения заданной сходимости.
На рис. 3 представлен график ![]() .
.
Как видно из графика рис. 3, при уменьшении отношения ( ![]() ) поправка (
) поправка (![]() ) стремится к 1, т.е., наклон секущей стремится к наклону касательной в начале координат, однако, как будет показано ниже, ошибка расчета при этом недопустимо велика. По мере увеличения расчетного интервала относительная величина поправки асимптотически стремится к величине относительного расчетного интервала.
) стремится к 1, т.е., наклон секущей стремится к наклону касательной в начале координат, однако, как будет показано ниже, ошибка расчета при этом недопустимо велика. По мере увеличения расчетного интервала относительная величина поправки асимптотически стремится к величине относительного расчетного интервала.
Определение зависимости погрешности расчета теплового потока от величины относительного расчетного интервала Δτ/a
Абсолютная величина средней квадратичной ошибки функции δ(f(x1, x2, x3, ...) нескольких переменных определяется как (/5/, с.365)
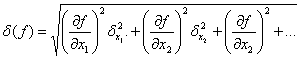 , (22)
, (22)
а относительная величина средней квадратичной ошибки σ(f) = δ(f)/f.
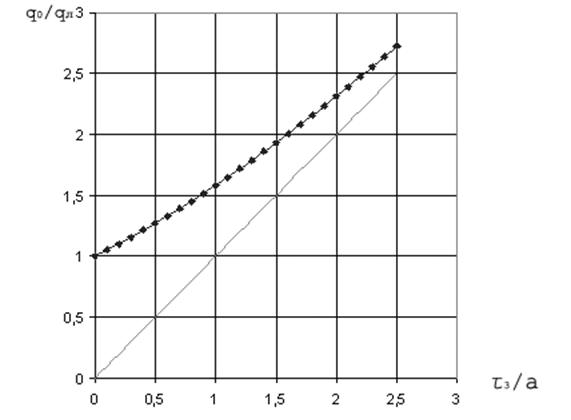
Рис. 3. Зависимость относительной величины поправки к qл от относительной величины времени измерения.
Определим величины средней квадратичной ошибки величин Х, а, и q в предположении, что в уравнении (11) Θi-1=0, т.е., для интервала, первая точка которого совпадает с τ0=0.
Используя уравнение (11), (14), (21) и обозначая (Δτ/а)=Y,
T3/T2 =[1-exp(-2Y)]/[1-exp(-Y)] =Z, получаем:
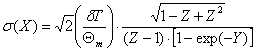 , (23)
, (23)
где δT - абсолютная величина погрешности измерения температуры датчика.
Далее, исходя из (14), имеем постоянной времени для относительной ошибки
![]() . (24)
. (24)
Если определяется ![]() как средняя величина по n участкам, то
как средняя величина по n участкам, то
![]() . (25)
. (25)
Величину среднеквадратичной ошибки σ(q) определяем с использованием уравнений (23)...(25).
![]() . (26)
. (26)
На рис. 4 представлена рассчитанная по уравнению (26) зависимость среднеквадратичной ошибки расчета теплового потока от относительной величины интервала времени (Y). При этом величина ![]() в уравнении (26) принята, для примера, равной 0,001, что соответствует величинам погрешности измерения температуры 1,0 К при величине Θm =1400 К.
в уравнении (26) принята, для примера, равной 0,001, что соответствует величинам погрешности измерения температуры 1,0 К при величине Θm =1400 К.
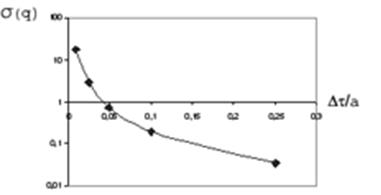
Рис. 4. Зависимость относительной среднеквадратичной ошибки расчета теплового потока от относительной величины интервала времени между соседними измерениями
Рассмотрим условия достижения минимальной погрешности расчета величины теплового потока. Как видно из графика, погрешность расчета теплового потока резко увеличивается при уменьшении интервала Δτ/а. Поэтому целесообразно выбирать точку τ3 как соответствующую максимальной температуре на расчетном интервале.
При определении рабочего диапазона термограммы, соответствующего условию X~const, целесообразно иметь подробную картину. Однако, как можно найти из анализа уравнений (23) и (25), с дроблением рабочего диапазона на n участков погрешность величин X и а возрастает. Поэтому следует оптимизировать число элементарных участков в каждом конкретном эксперименте.
Оптимизация осреднения по временнóму интервалу замеров
При большой частоте измерений, что имеет место, прежде всего, в случае регистрации данных с помощью аналого-цифрового преобразователя и компьютера, разность температур в соседних точках соизмерима с погрешностью измерений, что ведет к большой погрешности при определении как величин "X" по уравнению (11) и, соответственно, постоянной времени, "а" по уравнению (12), так и плотности теплового потока q0 по уравнению (21)
Поэтому в алгоритме расчетная величина температуры определяется как средняя из k измерений на интервале времени ![]() . С увеличением k уменьшается статистическая погрешность, но растет систематическая погрешность, связанная с тем, что средняя на интервале времени
. С увеличением k уменьшается статистическая погрешность, но растет систематическая погрешность, связанная с тем, что средняя на интервале времени ![]() температура меньше действительной температуры на середине интервала температуры, которая входит в расчеты.
температура меньше действительной температуры на середине интервала температуры, которая входит в расчеты.
Поэтому целесообразно выбирать такое число точек осреднения, чтобы систематическая погрешность была не больше статистической погрешности средней температуры на этом интервале.
Определим это соотношение систематической и статистической погрешностей на участке из k элементарных временных интервалов. Здесь числовые индексы относятся не ко всему процессу, а к участку осреднения.
Как известно, средняя квадратичная ошибка ряда измерений обратно пропорциональна квадратному корню из числа измерений, тогда погрешность осреднения равна:
![]() . (27)
. (27)
Теперь определим ошибку сглаживания.
Согласно (7), температура в середине интервала от τ0 на термограмме ![]() равна:
равна:
![]() . (28)
. (28)
Средняя величина температуры, измеренной на участке от τ0 до τk-1 может быть представлена в виде:
![]() . (28)
. (28)
Далее, используя формулу для суммы членов геометрической прогрессии, получим:
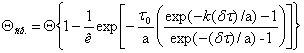 . (29)
. (29)
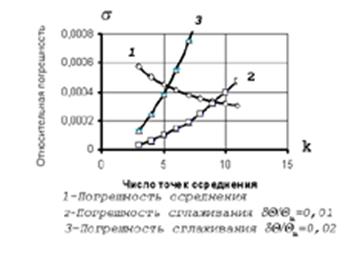
Рис. 5. Изменение погрешности осреднения и погрешности сглаживания в зависимости от количества точек осреднения и времени между соседними измерениями при ![]() ,
, ![]() и
и ![]() .
.
Тогда, очевидно, соотношение для расчета погрешности за счет сглаживания можно представить в виде:
![]() . (30)
. (30)
Определим погрешность сглаживания для первого интервала, где, в начале интервала, τ0=0 и Θ1=0.
На рис. 5 показано изменение погрешности осреднения и погрешности сглаживания в зависимости от числа точек осреднения. При этом относительная погрешность отдельного измерения температуры составляла ![]() , а относительный размер межточечного интервала времени между соседними измерениями принимался
, а относительный размер межточечного интервала времени между соседними измерениями принимался ![]() и
и ![]() .
.
Как видно из графика, число точек, по которым производится осреднение, должно уменьшаться с увеличением межточечного интервала времени. При ![]() оно не должно превышать восьми, а при
оно не должно превышать восьми, а при ![]() - пяти.
- пяти.
СПИСОК ЛИТЕРАТУРЫ:
-
1. Григорович Б.М., Назаренко И.П., Никитин П.В., Сотник Е.В. «Определение теплового потока к теплоёмкостному (таблеточному) датчику регулярного режима по дискретным значениям его температуры». [Текст]//Современные проблемы образования и науки.- 2007-№6.-С.37.
-
2. Лыков А.В. Теория теплопроводности [Текст]. - М.: Высшая школа, 1967. 599 с.
-
3. Никитин П.В. «Тепловая защита» [Текст] - М.: Изд. Высш. школа, МАИ, 2006.
-
4. Кондратьев Г.М. «Тепловые измерения» [Текст] - М., Л.: Машгиз, 1957.
-
5. Гутер Р.С., Овчинский Б.В. Элементы численного анализа и математической обработки результатов опыта [Текст] - М.: Наука, 1969.



