Введение
В настоящее время для управления различными объектами часто используются команды, передаваемые объекту управления по радиоканалу. При этом в большинстве случаев правильность передачи команд по каналу, в котором на передаваемый сигнал действуют разного рода помехи, оказывается критичным. Одним из наиболее эффективных подходов, позволяющих решить задачу обеспечения требуемой достоверности передачи радиокоманд, является применение помехоустойчивого кодирования.
Известно, что на сегодняшний день существует большое число кодов и методов их декодирования, различающихся корректирующей способностью, вносимой избыточностью, сложностью реализации и многими другими важными параметрами [4]. И для конкретной системы связи требуется выбирать лучшие коды с учетом накладываемых ограничений. Например, в известной авторам системе передачи команд управления по КВ-каналам используются сообщения с информационной длиной 1600 битов, допустима кодовая скорость используемых кодов 2/5 и выше, применяется модуляция типа BPSK, возможно использование только жестких решений демодулятора, декодер реализуется в программном виде. В данной системе требуется обеспечить вероятность безошибочного приема радиокоманды (вероятность ошибки на блок) не менее 0.95 при вероятности ошибки в канале порядка 8…9%. При этом применяемые в настоящее время помехоустойчивые коды позволяют получить данную вероятность правильного приема только при вероятности ошибки в канале 0.067.
Цель исследования
Анализ известных помехоустойчивых кодов и методов их декодирования показал, что в наибольшей степени обеспечить подобные требования могут многопороговые декодеры (МПД) самоортогональных кодов (СОК) [1-3]. Данные методы обладают малой сложностью, что допускает их высокоскоростную практическую реализацию даже на цифровом сигнальном процессоре. Использование других методов коррекции ошибок, таких как турбо и низкоплотностные коды, представляется нецелесообразным, поскольку они значительно сложнее для реализации и для получения наилучшей эффективности требуют наличия оценок надежности решения демодулятора для каждого принятого бита.
Рассмотрим выбранные методы коррекции ошибок более подробно, после чего выберем параметры кода, который позволит обеспечить обозначенные требования, и выполним исследование его эффективности с помощью компьютерного моделирования.
Материал и методы исследования
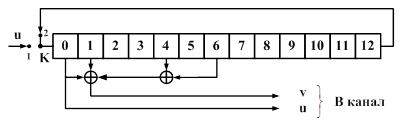
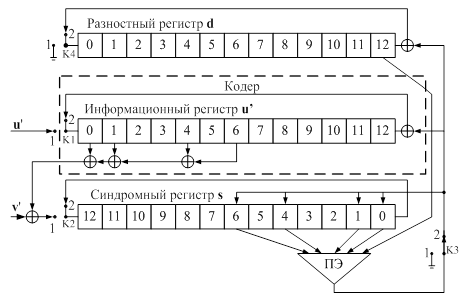
Для иллюстрации основных принципов работы МПД, используемого для декодирования блоковых или сверточных самоортогональных кодов (СОК), рассмотрим схемы, реализующие операции кодирования и декодирования. Кодер для подобных кодов является простейшим устройством, состоящим только из регистров сдвига и сумматоров по модулю 2. Пример кодера для блокового СОК с кодовой скоростью R=1/2 и длиной 26 битов показан на рис. 1а. Достаточно простым для реализации является и сам МПД, пример схемы которого для такого же блокового кода показан на рис. 1б [1-3].
а)
б)
Рис. 1. Схема кодера и декодера МПД блокового кода
Опишем принципы работы кодера СОК на примере представленной на рис. 1 схемы. В процессе работы кодер формирует проверочные символы в соответствии со следующим алгоритмом.
- Перед началом кодирования кодового блока ключ K находится в состоянии 1.
- Информационный вектор u = (u0, u1, …, u12) посимвольно подается на вход регистра сдвига. Пусть в результате информационный символ u0 располагается в ячейке 12, u1 – в ячейке 11 и т.д.
- Ключ K переводится в состояние 2.
- Для j от 0 до 12 выполняется циклический сдвиг регистра, поле чего вычисляется j-й проверочный символ vj:
![]() .
.
В результате выполнения алгоритма формируется проверочный вектор v = (v0, v1, …, v12), который вместе с информационным вектором образует кодовое слово c=(u,v), передаваемое по каналу.
Далее опишем основные принципы работы многопорогового декодера [2].
Пусть после передачи по двоичному симметричному каналу (ДСК) декодер получает вместо кодового слова c искаженное шумами сообщение y=(u’,v’) длины n. Сначала, как и в обычном пороговом декодере, вычисляется синдром s=Hy (здесь H – проверочная матрица кода) принятого сообщения, и для каждого информационного символа uj, 1£j£k, выделяется множество {sp} элементов синдрома Qj, называемых проверками относительно символа uj и содержащих в качестве слагаемого ошибку ej в этом символе.
Двоичный вектор d длиной k, называемый разностным, первоначально заполняется нулями. В данном векторе будут отмечаться измененные информационные символы для того, чтобы декодер «помнил» принятое из канала сообщение и всегда мог вычислить разность между этим сообщением и кодовым словом, находящимся в информационном регистре.
Основной шаг декодирования заключается в том, что для произвольно взятого символа uj вычисляется функция правдоподобия Lj, зависящая от относящихся к нему проверок и j-го элемента вектора d:
![]() , (1)
, (1)
где dj – символ разностного вектора, относящийся к декодируемому символу uj (равный 0 или 1); sp – p-й элемент вектора синдрома, входящий во множество проверок относительно декодируемого символа uj; Qj – множество номеров проверок, контролирующих j-й информационный символ.
Общее число слагаемых в (1) равно кодовому расстоянию d. Если Lj>T, где T=(d–1)/2 – пороговое значение, то символ uj, все участвующие при получении Lj проверки и символ dj инвертируются, после чего выбирается другой символ um, m¹j, для него снова вычисляется сумма Lm и т.д. Если же Lj£T, то сразу осуществляется переход к декодированию следующего символа um.
В [2] показано, что основным свойством МПД является строгое приближение его решения к решению оптимального (по максимуму правдоподобия) декодера при каждом изменении декодируемого символа. Это определяется тем, что при изменении символа суммарный вес синдрома s и разностного вектора d обязательно уменьшается и, таким образом, происходит переход к кодовому слову, которое более правдоподобно, чем кодовое слово, находившееся в МПД в предыдущий момент времени.
Выбор параметров многопорогового декодера для обеспечения требования системы передачи команд управления по радиоканалу
В соответствии с требованиями, предъявляемыми к системе передачи радиокоманд управления, необходимо обеспечить вероятность правильного декодирования 0.95 и более (вероятность ошибочного блока 0,05 и менее) при 8…9% ошибок в канале связи. При этом предполагается, что ошибки в канале появляются независимо друг от друга и с равной вероятностью, т.е. можно использовать модель двоичного симметричного канала (ДСК). Оценим параметры кода (в данном случае нас интересует только минимальное кодовое расстояние), который сможет обеспечить такие характеристики.
В худшем случае, если предположить, что ошибки в декодированных блоках появляются независимо друг от друга, вероятность ошибки в блоке длиной 1600 битов определяется выражением
![]() , (2)
, (2)
где Pb – вероятность битовой ошибки декодирования. Из данной формулы следует, что для обеспечения вероятности ошибки декодирования на блок не более 0.05 требуется обеспечить вероятность ошибки декодирования на бит не менее 3.2·10–5.
Для МПД известно, что с его помощью можно обеспечить вероятность ошибки декодирования, близкую к вероятности ошибки декодирования, обеспечиваемую оптимальным декодером и оцениваемую как
![]() , (3)
, (3)
где d – кодовое расстояние СОК (нечетное); p0 – вероятность ошибки в канале.
Из (3) следует, что требуемые характеристики при p0=0.08…0.09 способны обеспечить коды с кодовым расстоянием d, равным 13 или 15. Нами был построен и исследован ряд СОК с такими значениями d и кодовой скоростью 4/10, содержащих 4 информационных и 6 проверочных ветвей, среди которых были выбраны два лучших кода с кодовым расстоянием 13 и 15. Далее представим результаты их исследования.
Результаты исследования и их обсуждение
На рис. 2 показана зависимость вероятности ошибки МПД с 30 итерациями декодирования на блок от вероятности ошибки в канале типа ДСК для построенных кодов. Отметим, что код с кодовым расстоянием 15 позволяет обеспечить требуемую вероятность ошибки декодирования на блок, равную 0.05 при вероятности ошибки в канале 0.09, а код с кодовым расстоянием 13 – при вероятности ошибки в канале 0.085. Также видно, что код с кодовым расстоянием 15 оказывается лучше, чем код с кодовым расстоянием 13, при вероятности ошибки в канале 0.095 и меньшей. Это объясняется тем, что ошибки в блоке после его декодирования не являются независимыми. Т.е. если кодовый блок содержит ошибки, то их обычно несколько. Заметим, что в области эффективной работы МПД (при вероятности ошибки декодирования на блок 0.1 и менее) ошибки в принятом блоке в основном оказываются одиночными. Поэтому при необходимости уменьшения вероятности ошибки декодирования на блок можно использовать каскадирование СОК с кодами с контролем четности, позволяющее на 1…2 порядка уменьшить вероятность ошибки [3].
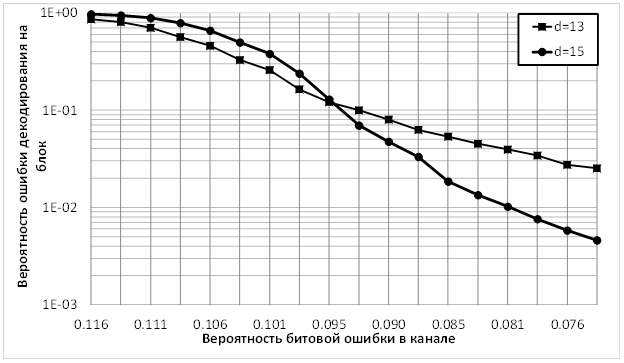
Рис. 2. Вероятность ошибки декодирования на блок в ДСК
На рис. 3 кривыми 1 и 2 для удобства показана зависимость вероятности правильного декодирования блока от вероятности ошибки в канале типа ДСК для построенных кодов. Выводы совпадают с выводами из предшествующего рисунка.
Заметим, что выбранные коды при благоприятных условиях приема (малый шум в канале) могут быть легко изменены на коды с более высокими кодовыми скоростями 4/9, 4/8, 4/7, 4/6, 4/5. Так можно осуществлять управление долей полезной информации в передаваемом потоке данных. Декодер при этом не меняется.
Возможности МПД для кодов с высокими кодовыми скоростями (т.е. с малой избыточностью) иллюстрируются на рис. 3 кривыми 3 и 4, которые показывают характеристики МПД для кодов с кодовой скоростью 4/7 и 4/6. Требуемая вероятность правильного приема блока 0.95 обеспечивается при вероятности ошибки в канале 0.037 и 0.022 соответственно, что является хорошим результатом. Заметим, что это только первоначальные результаты для самых простых из построенных кодов, которые в дальнейшем могут быть еще существенно улучшены.
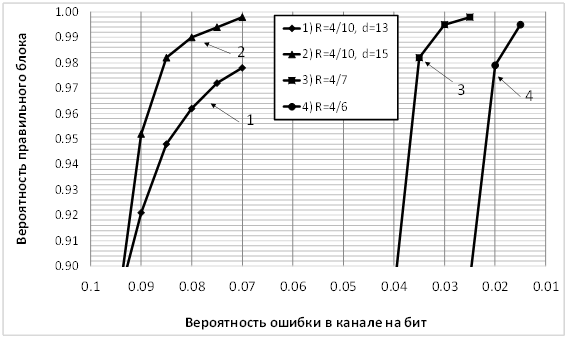
Рис. 3. Вероятность правильного приема блока в ДСК
Выводы
В результате проведенной работы показано, что за счет использования многопорогового декодера самоортогональных кодов при передаче команд управления по радиоканалам можно обеспечить увеличение вероятности ошибки, при которой достигается вероятность правильно принятого блока 0.95, с величины 0.067, получаемой классическими методами коррекции ошибок, до 0.09. За счет этого можно улучшить многие параметры системы управления, такие как дальность связи, скорость и надежность передачи и другие. Отметим, что хотя представленные расчеты и исследования выполнены для конкретных требований системы передачи команд управления, они легко адаптируются и под другие требования [5].
Рецензенты:
Кузнецов А.Е., д.т.н., профессор, зам. дир. НИИ «Фотон», ФГБОУ ВПО «Рязанский государственный радиотехнический университет», г. Рязань.
Костров Б.В., д.т.н, профессор кафедры ЭВМ, ФГБОУ ВПО «Рязанский государственный радиотехнический университет», г. Рязань.



