Введение
При геометрическом моделировании часто исходная информация имеет вид случайных величин, подчиненных нормальному закону распределения ошибок. Фиксация и обработка такой информации рассматриваются в теории вероятностей и теории нечетких множеств. Классическая проективная геометрия не учитывает ошибки, отклонения от перпендикулярности, параллельности или прямолинейности. Она использует идеальные точки и прямые. Для повышения точности моделирования требуется учитывать особенности исходной информации. Поэтому требуется модификация проективной геометрии, учитывающая свойства нечеткой геометрической информации.
Основные понятия
Особенностью проективного пространства является [5] то, что для него справедливы следующие утверждения:
а) каждая прямая проективного пространства содержит одну бесконечно удаленную точку;
б) каждая плоскость содержит одну бесконечно удаленную прямую;
в) проективное пространство в целом содержит одну бесконечно удаленную плоскость.
Для краткости бесконечно удаленные элементы будем дальше называть несобственными.
Основные объекты и основные отношения нечеткой проективной геометрии выражаются терминами «нечеткая точка», «нечеткая прямая», «нечеткая плоскость», «принадлежность». Точка представляется эллиптической областью, центр которой является ее номинальным положением, а границей – заданная ошибка (рис 1), описываемая нормальным законом распределения. Собственная двухмерная нечеткая точка изображается в виде эллипса рассеивания, который задается пятью параметрами: центр эллипса – 
, угол наклона большой оси эллипса к оси абсцисс (0X) – 
, большой и малой полуоси эллипса –.
,
. Этот эллипс представляет собой область, где данная точка может находиться с заданной вероятностью. Прямая – это область, ограниченная ветвями гиперболы, где она может находиться с заданной вероятностью. Номинальное положение прямой – мнимая ось гиперболы [3]. Мнимая ось гиперболы проходит через центры эллиптических областей, представляющих точки. Любой геометрический элемент представлен нечеткой областью. Пересечение нечетких элементов есть нечеткий элемент. Например, точкой пересечения пары прямых является точка-область, где эта точка пересечения может появиться с заданной вероятностью.
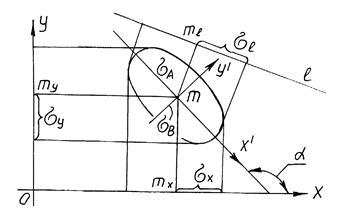
Рис.1. Собственная двухмерная нечеткая точка
Результаты построения точки схода (точки – области) обрабатываются методами математической статистики. Но прежде чем переходить к операциям с двухмерной нечеткой проективной геометрией, следует рассмотреть одномерную.
Одномерная нечеткая проективная геометрия
Это геометрия в пространстве, имеющем одно измерение, например, на прямой линии. Основным объектом одномерного проективного пространства является нечеткая точка, основным отношением – принадлежность. Проективная прямая содержит одну несобственную нечеткую точку.
Пусть 
– одномерная собственная точка,
– дополнение одномерной несобственной точки.
Одномерная точка называется собственной, если находится на конечном расстоянии от начала координат, и несобственной, соответственно, если находится в бесконечности. Собственная точка 
задается двумя параметрами: 
– математическое ожидание и 
– среднее квадратичное отклонение. Несобственная точка 
задается своим дополнением: 
– математическим ожиданием в начале координат и 
– среднее квадратичное отклонение.
В прикладных задачах, как правило, 
– достаточно большое число, выбираемое в зависимости от условий задачи (например, 
).
Принимаем, что закон распределения координат точки есть нормальный закон распределения (рис. 2), который характеризуется плотностью вероятности вида:
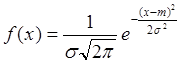, (1)
где 
– математическое ожидание или центр рассеивания,
– среднее квадратичное отклонение.
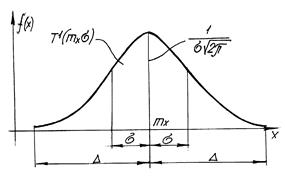
Рис. 2. Нормальный закон распределения координат точки
Учитывая общее требование к точности, в качестве величины математического ожидания принимается номинальное значение точки, а в качестве величины 
принимаем величину 
=
, где 
– заданный допуск измерения. При этом согласно правилу 3 сигм, только 0.27 % реальных отклонений превысят заданный допуск .
Данная гипотеза является общепринятой в экспериментальных исследованиях [1].
Чтобы применить общий подход теории нечетких множеств, рассмотрим в качестве универсального множества
. (2)
В качестве функции принадлежности, учитывая нормальный закон распределения рассматриваемых в работе величин, целесообразно выбрать функцию
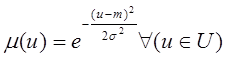. (3)
Нечеткой точкой с параметрами 
на прямой называется подмножество 
такое, что
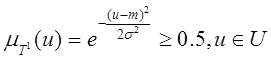. (4)
Подмножество 
также называется нечетким подмножеством, соответствующим нечеткой точке с параметрами .
Легко установить, что функция принадлежности изменяется в интервале [0,1] и ставит в соответствие каждому элементу 
число 
из интервала [0,1] (рис. 3).
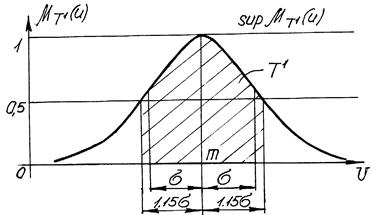
Рис. 3. Собственная одномерная нечеткая точка
Точками перехода, то есть значениями, 
для которых 
= 0.5, являются
, 
. (5)
Из (2) следует также, что максимальное значение функции принадлежности достигается при u=m, то есть
. (6)
Из (4) следует простое условие принадлежности
, (7)
где 
– точки перехода (5).
Несобственная нечеткая точка 
задается своим дополнением 
. Принимая это во внимание, сформулируем определение.
Нечеткой несобственной точкой на прямой называется подмножество 
такое, что
, (8)
где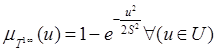 
– функция принадлежности нечеткому множеству 
(нечеткая несобственная точка) (рис 4).
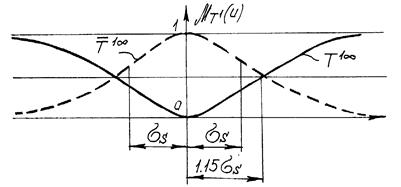
Рис. 4 Несобственная нечеткая одномерная точка и ее дополнение
Точками перехода этого множества является
, (9)
высота нечеткого множества равна
при 
.
Из (1.8) следует простое условие принадлежности
, (10)
где – точки перехода (9).
Точки в одномерном пространстве в проективной геометрии находятся в некоторой связи, которую принято выражать словами инцидентность [5] или принадлежность. Инцидентность в классической проективной геометрии имеет два значения, 0 (нет) и 1 (да). Например, если расстояние между точками равно нулю, то инцидентность двух точек равна 1(да), во всех остальных случаях инцидентность равна 0 (нет).
Взаимосвязь нечетких точек в одномерном пространстве так же будем обозначать термином, принадлежность или совпадение в нечетком смысле. Однако в отличие от классического случая степень принадлежности может принимать любые значения в интервале [0;1].
Назовем мерой принадлежности двух собственных точек величину.
(11)
где 
функция принадлежности нечеткому множеству 
,
функция принадлежности нечеткому множеству 
.
В соответствии с (3) и (11) принадлежность подсчитывается по формуле
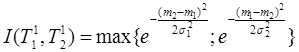. (12)
Из (12), если положить 
(13), следует:
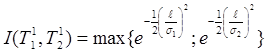, (14)
где 
– расстояние между математическими ожиданиями нечетких точек (см. рис. 5).
Назовем мерой принадлежности собственной и несобственной нечетких точек величину
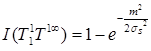, (15)
где m – математическое ожидание собственной точки,
– среднее квадратичное отклонение дополнения несобственной ночки 
.
Две нечеткие точки на прямой назовем принадлежными, если 
, и не принадлежными, если 
.
Примеры
Пример 1. (Рис. 5). Даны две собственные нечеткие точки:
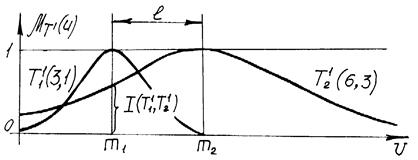
Рис. 5. Принадлежность двух собственных одномерных нечетких точек
(3,1) с параметрами 
, 
, 
(6,3) с параметрами 
, 
.
Требуется определить меру принадлежности этих двух точек, а также определить, принадлежны они или не принадлежны.
Расстояние между математическими ожиданиями 
. Мера принадлежности двух нечетких точек 
согласно (14) равна:
I(
)=max {0.01, 0.606}=0.606.
Нечеткие точки 
принадлежны потому, что мера принадлежности I(
)>0.5.
Пример 2. (Рис. 6). Две нечеткие точки.
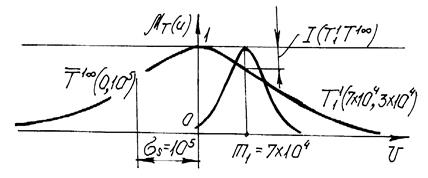
Рис. 6. Принадлежность собственной и несобственной одномерных нечетких точек
собственная точка с параметрами 
, 
, 
не собственная точка с параметрами 
, 
.
Требуется определить меру принадлежности этих двух точек, а также определить, принадлежны они или не принадлежны.
Мера принадлежности нечетких собственной и несобственной точек 
согласно (15) равна I=1 - 0.782=0.218.
Нечеткие точки не принадлежны потому, что мера принадлежности I()>0.5.
Заключение
Аналогично можно рассмотреть и двухмерную проективную нечеткую геометрию. Проективная плоскость в двухмерной проективной нечеткой геометрии содержит одну несобственную нечеткую прямую. Две нечеткие прямые на плоскости пересекаются в одной нечеткой точке. Основные объекты этой геометрии будут рассмотрены в следующей статье.
Сформулированные предложения по теории нечеткой проективной геометрии дали возможность разработать ряд алгоритмов решения задач геометрического моделирования утраченных памятников архитектуры по их перспективным изображениям [2]. Применение нечеткой проективной геометрии и статистической обработки результатов опытов при учете неравноточности измерений позволило увеличить достоверность результатов восстановления [4].
Рецензенты:
Рогов А.А., д.т.н., профессор, заведующий кафедрой теории вероятностей и анализа данных математического факультета Петрозаводского государственного университета, г. Петрозаводск.
Колесников Г.Н., д.т.н., профессор, заведующий кафедрой механики строительного факультета Петрозаводского государственного университета, г. Петрозаводск.