Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Введение

В современном мире довольно стремительно развивается вычислительная техника, которая находит применение во многих областях человеческой деятельности, в том числе и на промышленном производстве. При этом часто используются системы автоматического распознавания (САР), являющиеся программно-аппаратными комплексами, решающими задачи идентификации реальных объектов с применением видео-датчиков.

Их основными задачами являются: предварительная обработка [2], обнаружение искомой области на изображении, классификация и распознавание. При этом техническое оснащение может отличаться, в зависимости от задач конкретной предметной области.

Скорость и точность работы САР в целом зависит как от аппаратной части, так и от выбранных алгоритмов. Немаловажным является этап предварительной классификации объектов на сцене. Эту задачу можно решить с помощью геометрических признаков [3], таких как периметр, площадь, величина углов (кривизна), но существуют ситуации, когда их оказывается недостаточно и возникает необходимость добавления новых характеристик [1]. Для удобства вычислений используемые признаки приводятся к нормированному виду.

Существует множество подходов к решению данной задачи. В статье предлагается подход к классификации выпуклых плоских геометрических фигур с использованием вектора признаков, представляющим собой набор безразмерных коэффициентов, характеризующих их форму, нормализованных определенным образом и имеющих общий диапазон значений от нуля до единицы.

Определения

Для решения задачи классификации выпуклых плоских геометрических фигур автором были предложены прямоугольный и диагональный коэффициент формы, коэффициенты диагональных отрезков.

Введем следующие определения:

Прямоугольный коэффициент формы, kПКФ, далее ПКФ, характеризует отношение меньшей стороны описанного вокруг фигуры прямоугольника к большей [4].

Область значений коэффициента находится в диапазоне (0;1]:

1. Отношение ширины и длины фигуры пропорционально отношению двух сторон квадрата, если , если ;

2. Отношение ширины и длины фигуры пропорционально отношению двух сторон прямоугольника , если ;

где a,b – длины сторон описанного прямоугольника.

ПКФ позволяет классифицировать фигуры по форме их «вытянутости», то есть на те, которые можно «вписать» в квадрат, и те, которые можно вписать в «прямоугольник» (в данной статье речь пойдет о первом типе фигур).

Главная диагональ фигуры (максимальный отрезок) – отрезок (рис. 1, а – e), соединяющий 2 точки контура фигуры и имеющий максимальную длину.

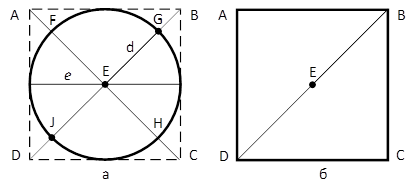
Рис. 1. Пример плоской геометрической фигуры, вписанной в квадрат

Диагональный коэффициент формы, – признак формы, вычисляющийся как отношение длины стороны описанного квадрата и главной диагонали фигуры [4].

Диагональные отрезки описанного квадрата, – отрезки (рис. 1, а – EB, EC, ED, EA), соединяющие центр описанного квадрата и его вершины [4].

Диагональный отрезок фигуры – отрезок (рис. 1 – EG, EF, EH, EJ), лежащий на одной из диагоналей описанного вокруг нее квадрата и соединяющий центр фигуры и точку пересечения ее контура с этой диагональю [4].

Коэффициенты диагональных отрезков, – отношения длин диагональных отрезков фигуры к длинам соответствующих диагональных отрезков описанного вокруг нее квадрата (EB, EC, ED, EA) [1].

Алгоритм классификации

Чтобы классифицировать фигуры, вписанные в квадрат, необходимо выполнить этапы:

1. Вычисляются следующие промежуточные величины:

– длина, ширина фигуры [3];

– длины диагональных отрезков по алгоритму, описанному в [4];

2 а. Находится ПКФ по формуле, представленной в [4];

2 б. Рассчитываются другие коэффициенты формы [4];

3. Выполняется проверка значения ПКФ:

– Если kПКФ = 1, то фигуру можно вписать в квадрат и выполняется пункт 4 алгоритма.

– Если 0 < kПКФ < 1, то фигуру можно вписать в прямоугольник (в данной статьей рассматривается только первый вариант).

4. Если фигура близка по форме к кругу, то ее диагонали будут практически равны между собой (диаметры), следовательно, →1.

Если фигура близка по форме к квадрату, то главная диагональ будет гипотенузой DB в прямоугольном треугольнике DBC, а сторона описанного вокруг фигуры квадрата будет совпадать с катетом DC данного треугольника и соответственно иметь такую же длину (рис. 1, б).

Отсюда:

где – длина соответствующего отрезка.

В прямоугольном треугольнике DNE:

,

,

Следовательно, для квадрата:

.

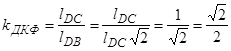Если , то есть главная диагональ и сторона описанного квадрата равны, то фигура является кругом (среди рассматриваемых типов фигур) (рис. 1а).

Таким образом, при (левое значение ДКФ описывают форму близкую к квадрату, правое – к кругу).

5. При распознавании более сложных фигур применяются коэффициенты диагональных отрезков.

В качестве примера были рассмотрены трапеция и параллелограмм. Найдены закономерности в значениях данных признаков у этих фигур.

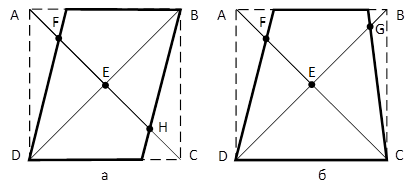
Рис. 2. Параллелограмм и трапеция, вписанные в квадрат

Для параллелограмма коэффициенты диагональных отрезков следующие:

;

;

;

;

Для трапеции:

;

;

;

Если выполняются следующие условия:

,

,

то трапеция будет равнобедренной.

Различие заключается в том, что в параллелограмме попарно равны коэффициенты противоположных диагональных отрезков, а в трапеции 2 смежных (рис. 2).

Исследование

По предложенному алгоритму были проведены исследования на тестовых геометрических фигурах. Целью исследования было экспериментальное подтверждение математических расчетов и сопоставление соответствующих значений коэффициентов отдельных фигур.

Было сгенерировано по 1500 фигур каждого типа формы из рассмотренных со случайно выбранными параметрами, характеризующими их размеры.

Все сгенерированные фигуры были распознаны верно. При генерации трапеции 47 % фигур были классифицированы как частные случаи (равнобедренная трапеция – коэффициенты смежных диагональных отрезков были попарно равны).

Средние значения коэффициентов, полученных в процессе исследования, представлены в таблице 1. Расчетные значения коэффициентов показаны в таблице 2. Комментарии к условным обозначениям в таблицах приведены ниже.

Таблица 1. Средние значения коэффициентов, полученных при помощи работы программы

Таблица 2 Расчетные значения признаков формы, вычисленные вручную

«-» – не рассчитываемый для данной фигуры коэффициент.

«л» – любое значение. .

В полях, обозначенных буквой «л», происходит сравнение между собой коэффициентов, либо сравнение со значениями частных случаев.

Заключение

Проведены испытания подхода к классификации плоских выпуклых геометрических фигур при помощи разработанной программы генератора изображений со случайными значениями параметров размера. Математически рассчитанные диапазоны значений параметров предложенных коэффициентов формы фигур были экспериментально подтверждены. В результате проведенных испытаний все фигуры были классифицированы верно.

Предложенный набор признаков можно применять для классификации объектов в САР на промышленных предприятиях при конвейерной сборке объектов [5, 6], у которых проекции на плоскость близки по форме к выпуклым геометрическим фигурам.

Рецензенты:

Юрков Н.К., д.т.н., профессор, заведующий кафедрой «Конструирование и производство радиоаппаратуры» Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Пензенский государственный университет» (ПГУ), г. Пенза.

Жиганов И.Е., д.т.н., профессор, заведующий кафедрой «Информационные системы и программная инженерия» Федерального государственного бюджетного учреждения высшего профессионального образования «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых» (ВлГУ), г. Владимир.