Введение
В работах [1-7] рассматривалась модель сделок с неполной информацией, где покупатель и продавец, случайно встретившись, определяли возможность осуществления сделки при конечном числе шагов. В работе [3] предложена и исследована следующая модель аукциона с конечным числом шагов. Зафиксируем временной горизонт ![]() . Выберем случайным образом продавца и покупателя на рынке. Предположим, что их резервные цены
. Выберем случайным образом продавца и покупателя на рынке. Предположим, что их резервные цены ![]() и
и ![]() есть независимые случайные величины, распределенные на интервале
есть независимые случайные величины, распределенные на интервале ![]() с непрерывными плотностями соответственно
с непрерывными плотностями соответственно ![]() и
и ![]() . На шаге
. На шаге ![]() игроки появляются на рынке и объявляют цену на товар (не обязательно совпадающую с резервными ценами). Мы будем считать их функциями от резервных цен, соответветственно
игроки появляются на рынке и объявляют цену на товар (не обязательно совпадающую с резервными ценами). Мы будем считать их функциями от резервных цен, соответветственно ![]() и
и ![]() . Сделка происходит, если
. Сделка происходит, если ![]() . Естественно считать, что
. Естественно считать, что ![]() и
и ![]() , т. е. продавец завышает, а покупатель занижает истинную оценку продукта, чтобы получить дополнительный доход от данной сделки. Если сделка состоялась, то будем считать, что она происходит по цене
, т. е. продавец завышает, а покупатель занижает истинную оценку продукта, чтобы получить дополнительный доход от данной сделки. Если сделка состоялась, то будем считать, что она происходит по цене ![]() , продавцы получают доход
, продавцы получают доход ![]() , а покупатели
, а покупатели ![]() . Если сделка не состоялась, игроки переходят на следующий шаг
. Если сделка не состоялась, игроки переходят на следующий шаг ![]() , покупатель (продавец) может изменить свое предложение и сделать его другому продавцу (покупателю). Мы считаем, что распределения резервных цен игроков не меняются. Стратегиями в данной байесовской игре являются функции
, покупатель (продавец) может изменить свое предложение и сделать его другому продавцу (покупателю). Мы считаем, что распределения резервных цен игроков не меняются. Стратегиями в данной байесовской игре являются функции ![]() и
и ![]() . Логично, что это неубывающие функции, поскольку чем больше затраты у продавца или оценка стоимости предмета у покупателя, то и предложения игроков должны быть больше. Были найдены дифференциальные уравнения и краевые условия для каждого шага, которым должно удовлетворять равновесие по Нэшу.
. Логично, что это неубывающие функции, поскольку чем больше затраты у продавца или оценка стоимости предмета у покупателя, то и предложения игроков должны быть больше. Были найдены дифференциальные уравнения и краевые условия для каждого шага, которым должно удовлетворять равновесие по Нэшу.
В данной работе эту конечношаговую модель двойного двухстороннего закрытого аукциона мы естественным образом обобщим для бесконечного числа шагов.
1. Двойной закрытый аукцион с бесконечным числом шагов
Введем коэффициент дисконтирования ![]() и рассмотрим аукцион с бесконечным временным горизонтом. Предположим, что резервные цены продавцов и покупателей
и рассмотрим аукцион с бесконечным временным горизонтом. Предположим, что резервные цены продавцов и покупателей ![]() и
и ![]() на шаге
на шаге ![]() распределены на интервале
распределены на интервале ![]() с непрерывными плотностями распределения соответственно
с непрерывными плотностями распределения соответственно ![]() и
и ![]() . На
. На ![]() -м шаге игроки используют стратегии
-м шаге игроки используют стратегии ![]() и
и ![]() . Если сделка состоялась, то покупатель
. Если сделка состоялась, то покупатель ![]() и продавец
и продавец ![]() получают доход
получают доход ![]() и
и ![]() соответственно и на следующий шаг не переходят. Кроме того, пусть на каждом шаге на рынке появляется фиксированное количество новых продавцов и покупателей с распределениями, не зависящими от номера шага. Исследование этой модели в общем случае представляется довольно трудным. Однако, логично ожидать, что при
соответственно и на следующий шаг не переходят. Кроме того, пусть на каждом шаге на рынке появляется фиксированное количество новых продавцов и покупателей с распределениями, не зависящими от номера шага. Исследование этой модели в общем случае представляется довольно трудным. Однако, логично ожидать, что при ![]() и оптимальном поведении игроков,
и оптимальном поведении игроков, ![]() и
и ![]() сходятся к неким предельным распределениям
сходятся к неким предельным распределениям ![]() и
и ![]() . Поэтому ограничимся исследованием стационарного состояния на рынке, когда распределения игроков
. Поэтому ограничимся исследованием стационарного состояния на рынке, когда распределения игроков ![]() и
и ![]() не меняются от шага к шагу, т. е. уход игроков, заключивших сделку, компенсируется приходом новых продавцов и покупателей.
не меняются от шага к шагу, т. е. уход игроков, заключивших сделку, компенсируется приходом новых продавцов и покупателей.
2. Интегро-дифференциальные уравнения для равновесия по Нэшу
Для нахождения оптимальных стратегий игроков воспользуемся следующими соображениями. Будем считать их функциями от резервных цен, соответственно ![]() и
и ![]() . Допустим, что это дифференцируемые и строго возрастающие функции. Тогда существуют обратные (тоже дифференцируемые и строго возрастающие) функции
. Допустим, что это дифференцируемые и строго возрастающие функции. Тогда существуют обратные (тоже дифференцируемые и строго возрастающие) функции ![]() и
и ![]() , т. е. соответственно
, т. е. соответственно ![]() и
и ![]() . Сделка происходит, если
. Сделка происходит, если ![]() . Если сделка состоялась, будем считать, что она происходит по цене
. Если сделка состоялась, будем считать, что она происходит по цене ![]() . Функции выигрыша игроков имеют вид (1) и (2), где математическое ожидание берется по соответствующим распределениям. Зафиксируем стратегию покупателя
. Функции выигрыша игроков имеют вид (1) и (2), где математическое ожидание берется по соответствующим распределениям. Зафиксируем стратегию покупателя ![]() и установим наилучший ответ продавца для различных значений параметра
и установим наилучший ответ продавца для различных значений параметра ![]() .
.
Условие ![]() эквивалентно
эквивалентно ![]() . Выигрыш продавца равен
. Выигрыш продавца равен
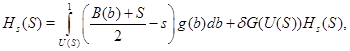
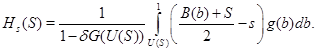 (1)
(1)
Дифференцируя (1) по ![]() , установим наилучший ответ продавца из (необходимого) условия равенства нулю производной выигрыша
, установим наилучший ответ продавца из (необходимого) условия равенства нулю производной выигрыша
![]()
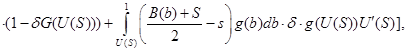
откуда получаем интегро-дифференциальное уравнение для определения оптимальных стратегий (точнее обратных фунций) ![]()
![]()
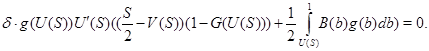
Аналогично, пусть ![]() стратегия продавца. Найдем наилучший ответ покупателя для различных значений параметра
стратегия продавца. Найдем наилучший ответ покупателя для различных значений параметра ![]() . Его выигрыш
. Его выигрыш
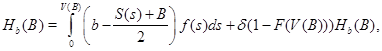
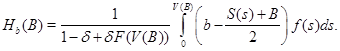 (2)
(2)
Дифференцируя (2) по ![]() , установим наилучший ответ покупателя из (необходимого) условия равенства нулю производной выигрыша
, установим наилучший ответ покупателя из (необходимого) условия равенства нулю производной выигрыша
![]()
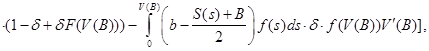
откуда получаем второе интегро-дифференциальное уравнение для определения оптимальных стратегий (точнее обратных фунций) ![]()
![]()
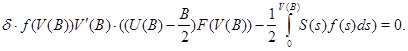
Запишем систему уравнений в разрешенном относительно производных виде
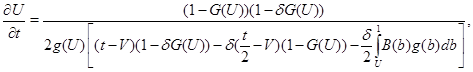 (3)
(3)
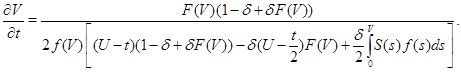 (4)
(4)
Функции ![]() и
и ![]() должны удовлетворять граничным условиям
должны удовлетворять граничным условиям ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Переходя к пределу в (3) и (4), легко находим, что
. Переходя к пределу в (3) и (4), легко находим, что
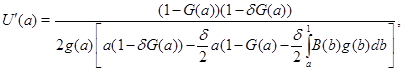 (5)
(5)
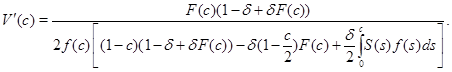 (6)
(6)
Также как и в одношаговой задаче [1,3-4], для нахождения маргинальных цен ![]() и
и ![]() воспользуемся следующими соображениями. Предположим, что существуют, конечны и больше нуля производная
воспользуемся следующими соображениями. Предположим, что существуют, конечны и больше нуля производная ![]() и плотность
и плотность ![]() . Тогда по правилу Лопиталя выводим, что
. Тогда по правилу Лопиталя выводим, что
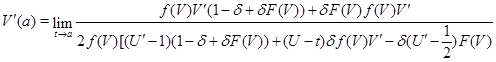
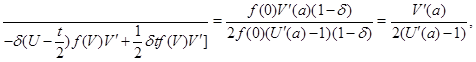
откуда следует, что ![]() .
.
Аналогично, пусть существуют, конечны и больше нуля производная ![]() и плотность
и плотность ![]() . Тогда по правилу Лопиталя получаем, что
. Тогда по правилу Лопиталя получаем, что
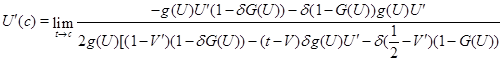
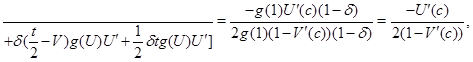
откуда вытекает, что ![]() .
.
Итак, мы нашли необходимое условие оптимальности для дифференцируемых строго возрастающих стратегий игроков. Заметим, что случай ![]() соответствует одношаговой задаче, подробно изученной в [1].
соответствует одношаговой задаче, подробно изученной в [1].
Теорема 1. Пусть плотности распределения ![]() и
и ![]() непрерывные на
непрерывные на ![]() ,
, ![]() ,
, ![]()
![]() существуют, конечны и больше нуля. Тогда дифференцируемые строго возрастающие стратегии
существуют, конечны и больше нуля. Тогда дифференцируемые строго возрастающие стратегии ![]() на
на ![]() и
и ![]() на
на ![]() , образующие равновесие по Нэшу в задаче о сделках с бесконечным горизонтом, определяются по системе (3),(4) на интервале
, образующие равновесие по Нэшу в задаче о сделках с бесконечным горизонтом, определяются по системе (3),(4) на интервале ![]() , с граничными условиями
, с граничными условиями ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Причем маргинальные цены
. Причем маргинальные цены ![]() и
и ![]() определяются из условий
определяются из условий ![]() ,
, ![]() , находимым по (5), (6).
, находимым по (5), (6).
3. Равновесие по Нэшу с пороговыми стратегиями участников
Необходимое и достаточное условие для пороговых стратегий являться равновесием по Нэшу дает следующая
Теорема 2. Пусть стратегии ![]() порогового типа с ценой
порогового типа с ценой ![]() , т.е.
, т.е. ![]() . Тогда они образуют равновесие по Нэшу в задаче о сделках с бесконечным временным горизонтом, тогда и только тогда, когда справедливы
. Тогда они образуют равновесие по Нэшу в задаче о сделках с бесконечным временным горизонтом, тогда и только тогда, когда справедливы
(![]() )
) ![]() имеет на
имеет на ![]() наибольшее значение при
наибольшее значение при ![]() ,
,
(![]() )
) ![]() на
на ![]() принимает наибольшее значение при
принимает наибольшее значение при ![]() .
.
Доказательство.
Сделка происходит, если резервная цена продавца ![]() , а предлагаемая им цена
, а предлагаемая им цена ![]() и
и ![]() . Выигрыш продавца (1) равен
. Выигрыш продавца (1) равен
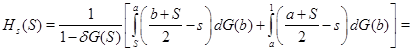
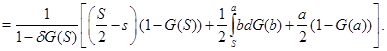 (7)
(7)
Нетрудно понять, что
![]()
откуда, учитывая монотонность ![]() , из (
, из (![]() ) следует, что для любого
) следует, что для любого ![]() выигрыш продавца достигает наибольшего значения при
выигрыш продавца достигает наибольшего значения при ![]() .
.
Аналогичные рассуждения можно провести для покупателей. Сделка происходит, если резервная цена покупателя ![]() , а предлагаемая им цена
, а предлагаемая им цена ![]() и
и ![]() . По формуле (2) найдем выигрыш покупателя
. По формуле (2) найдем выигрыш покупателя
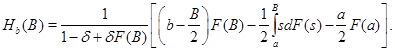 (8)
(8)
Заметим, что
![]()
откуда, учитывая монотонность ![]() , из (
, из (![]() ) следует, что для любого
) следует, что для любого ![]() выигрыш покупателя достигает наибольшего значения при
выигрыш покупателя достигает наибольшего значения при ![]() .
.
Замечание 1. Если ![]() имеют кусочно-непрерывные и ограниченные плотности
имеют кусочно-непрерывные и ограниченные плотности ![]() на
на ![]() и
и ![]() на
на ![]() , то в теореме 2 для (
, то в теореме 2 для (![]() ) достаточно выполнения
) достаточно выполнения
![]() (9)
(9)
а (![]() ) верно, если
) верно, если
![]() (10)
(10)
Доказательство.
В точках непрерывности ![]() , дифференцируя (7), находим
, дифференцируя (7), находим
![]()
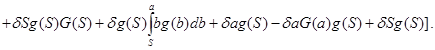 (11)
(11)
Учитывая, что
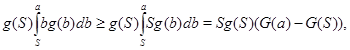
представляя ![]() , получаем, что в (11) выражение в квадратных скобках не меньше
, получаем, что в (11) выражение в квадратных скобках не меньше
![]()
![]()
и далее, так как ![]() и верно (9), следует
и верно (9), следует
![]()
Таким образом мы доказали, что производная выигрыша ![]() неотрицательна на
неотрицательна на ![]() , откуда и следует (
, откуда и следует (![]() ).
).
В точках непрерывности ![]() , дифференцируя (8), получаем
, дифференцируя (8), получаем
![]()
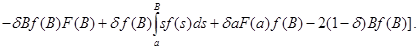 (12)
(12)
Замечая, что
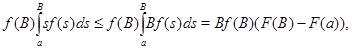
подставляя ![]() , выводим, что в (12) выражение в квадратных скобках не меньше
, выводим, что в (12) выражение в квадратных скобках не меньше
![]()
и далее, так как ![]() и верно (10), следует
и верно (10), следует
![]()
Т.е. мы доказали, что производная выигрыша ![]() неположительна на
неположительна на ![]() , откуда вытекает (
, откуда вытекает (![]() ).
).
Таким образом, при выполнении условий теоремы 2 сделка всегда происходит по фиксированной цене ![]() . Замечание 1 показывает, что для любой цены
. Замечание 1 показывает, что для любой цены ![]() при ограниченных плотностях распределения игроков
при ограниченных плотностях распределения игроков ![]() и при дисконтировании
и при дисконтировании ![]() достаточно близком к единице будет иметь место равновесие с фиксированной ценой
достаточно близком к единице будет иметь место равновесие с фиксированной ценой ![]() .
.
Пример 1 . Исследуем задачу при равномерном распределении игроков на интервале ![]() , т. е.
, т. е. ![]() ,
, ![]() . Так как
. Так как ![]() ,
, ![]() , то в Замечании 1 можно положить
, то в Замечании 1 можно положить ![]() . По (9), (10) находим, что при
. По (9), (10) находим, что при ![]() пороговые стратегии с ценой
пороговые стратегии с ценой ![]() образуют равновесие. При
образуют равновесие. При ![]() мы получаем достаточное (по Замечанию 1) условие
мы получаем достаточное (по Замечанию 1) условие ![]() .
.
Найдем точную границу для коэфициента дисконтирования ![]() . Производная выигрыша (11) в этом случае равна
. Производная выигрыша (11) в этом случае равна
![]()
откуда, решая соответствующее квадратное неравенство, легко выводим, что при
![]()
производная выигрыша продавцов неотрицательна. Следовательно, получаем необходимое и достаточное условие
![]()
решая которое, находим, что продавцов устроит цена
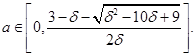
Аналогично получаем нижнюю границу цены сделки для покупателей
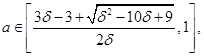
откуда, следует, что при ![]() пороговые стратегии с ценой
пороговые стратегии с ценой ![]() образуют равновесие по Нэшу в задаче о сделках с бесконечным числом шагов.
образуют равновесие по Нэшу в задаче о сделках с бесконечным числом шагов.
Заключение
В настоящей работе предлагается многошаговая модель двойного закрытого аукциона. Распределение резервных цен на рынке известно всем участникам. На каждом шаге случайным образом выбирается пара агентов с разными резервными ценами, которые решают осуществлять сделку или нет. В классической постановке, это одноактный процесс. Такая постановка исследовалась в работах Чаттерджи и Самуэльсона и нобелевского лауреата Майерсона. В предложенной модели, если сделка не происходит, агенты переходят на следующий шаг. При этом происходит дисконтирование платежей.
Ищется равновесие по Нэшу в данной игре. Стратегиями являются функции от резервных цен, т.е. в зависимости от резервной цены агенты предлагают тот или иной вариант для сделки с целью максимизировать свой доход. Предполагая, что существует стационарное состояние в этой модели при большом интервале аукциона, исследуется каким должно быть равновесие в данной задаче. Его свойства представлены в теоремах 1 и 2. В первой теореме приводится система интегро-дифференциальных уравнений с граничными условиями, из которых могут быть найдены строго монотонные равновесные стратегии. Во второй теореме приводятся условия, при которых равновесие лежит среди пороговых стратегий.
Работа выполняется при финансовой поддержке Программы стратегического развития ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности. Работа выполнена при финансовой поддержке РФФИ (проекты 13-01-00033-а, 13-01-91158-ГФЕН_а).
Рецензенты:
Мазалов В.В., д.ф.-м.н., профессор, директор Института прикладных математических исследований Карельского научного центра РАН, г.Петрозаводск.
Рогов А.А., д.т.н., профессор, заведующий кафедрой ТВиАД Петрозаводского государственного университета, г.Петрозаводск.
Криштоп В.В., д.ф.м.н., профессор, заведующий кафедрой «Физика», Дальневосточный государственный университет путей сообщения, г. Хабаровск, профессор Университета Kwangwoon University, Korea.



