При моделировании обтекания в аэродинамической трубе имеют место ряд факторов, обуславливающих искажение полученных результатов. К таким факторам относятся загромождение трубы, неподвижность поверхности, моделирующей полотно дороги, погрешность измерения. Другой сложностью также является ограниченность числа Рейнольдса, определяемого имеющимся оборудованием. Как известно, данный критерий подобия определяется соотношением (1)
![]() , (1)
, (1)
где ![]() – плотность газовой смеси,
– плотность газовой смеси, ![]() – скорость потока,
– скорость потока,![]() – характерная длина,
– характерная длина, ![]() – аэродинамическая вязкость.
– аэродинамическая вязкость.
Характеристики аэродинамической трубы НГТУ [3] обеспечивают реальную скорость 35 м/с, но её размеры (площадь сопла – 0,54 м2, длина рабочей части – 1 м) позволяют продувать только уменьшенные модели автомобилей. Компенсировать уменьшение размеров обтекаемого тела за счёт использования среды с большей динамической вязкостью и плотностью не представляется возможным ввиду открытости рабочей области [4]. Для определения степени влияния отклонения числа Рейнольдса были проведены эксперименты на аэродинамической трубе НГТУ.
В данной статье предлагается исследовать влияния числа Рейнольдса на коэффициент лобового сопротивления на основе серии экспериментов различными значениями этого числа. На рис.1 показан вид аэродинамической трубы с установленной моделью автомобиля для проведения эксперимента.

Рис. 1. Аэродинамическая труба с установленной моделью автомобиля
Объект исследования устанавливается на аэродинамические весы и размещается в рабочей части трубы. Сверху опускается металлическая плита, имитирующая дорожное полотно. На микроамперметрах, используемых для измерения действующих на модель сил (сопротивления, подъёмной силы и опрокидывающего момента). Для измерения величины сил, соответствующих показаниям микроамперметров, производится тарировка, алгоритм проведения которой более подробно описан в работе [5]. После проведения всех необходимых подготовительных действий включается вентилятор аэродинамической трубы и с помощью трубки Пито – Прандтля и показаний чашечного манометра устанавливается требуемая в эксперименте скорость [1]. После того, как течение в аэродинамической трубе установится, записываются показания с измерительно-регистрирующего комплекса. Эксперимент повторяется для каждого значения скорости и исследуемой модели.
Ключевыми результатами измерения в данной серии экспериментов были значения перепада давления согласно показаниям манометра и лобовое сопротивление. Как видно из рис. 1, на силу сопротивления существенно влияют элементы крепления, поэтому необходимо учитывать это влияние. В связи с необходимостью проведения серии экспериментов с различными значениями скоростей, измерение силы сопротивления крепления без моделей проводились только для максимального значения скорости потока. Для анализа остальных экспериментов авторы данной статьи предполагали, что доля сопротивления, приходящаяся на крепление, зависит только от продуваемой модели, но не от скорости потока. Согласно проведённым экспериментам, для конфигураций обтекаемого тела, представленных в работе, вклад креплений в силу лобового сопротивления всей системы составил 34–36 %.
Для вычисления скорости потока использовалась следующая формула:
![]() ,
,
где ![]() – динамическое давление, кПа;k – градировочный коэффициент манометра, учитывающий наклон отсчетной трубки манометра; h – показание манометра, кПа;
– динамическое давление, кПа;k – градировочный коэффициент манометра, учитывающий наклон отсчетной трубки манометра; h – показание манометра, кПа;![]() – плотность воздуха кг/м3.
– плотность воздуха кг/м3.
Для вычисления коэффициента аэродинамического (лобового) сопротивления использовано соотношение [2]
![]() ,
,
где F – сила сопротивления с учётом поправки на крепление модели, Н; S – площадь поперечного сечения исследуемого объекта, м2.
Число Рейнольдса, как известно, определяется согласно соотношению
![]()
где L – длина объекта, м; ![]() – вязкость воздуха, м2/с.
– вязкость воздуха, м2/с.
При обработке результатов эксперимента использовались следующие значения: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
В таблице 1 показана конфигурация и названия исследуемых в данной работе моделей.
Таблица 1
Конфигурации продуваемых моделей
|
Модель 3 седан |
Модель 3 хетчбек |
Модель 3 универсал |
Модель 1 седан |
|
|
|
|
|
На рис.1–4 представлены результаты расчётов коэффициента лобового сопротивления, основанные на экспериментальных данных. Для определения характера изменения коэффициента лобового сопротивления с ростом числа Рейнольдса была выбрана линейная аппроксимация. Из рисунков видно, что полученная зависимость хорошо согласуется с экспериментальными данными с отклонением не более 5 %. Как видно из рисунков, модель 1 седан имеет наименьший коэффициент Cx при максимальных значениях числа Рейнольдса. При этом именно для неё коэффициент аэродинамического сопротивления в наибольшей степени зависит от числа Рейнольдса.
.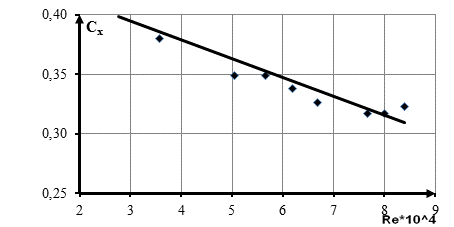
Рис.1. Зависимость Сх от числа Re для модели 3 седан
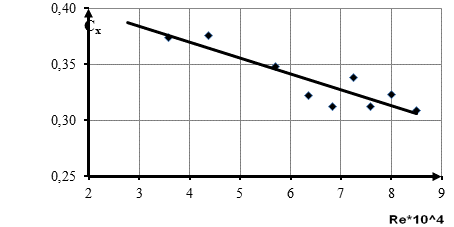
Рис.2. Зависимость Сх от числа Re для модели 3 хетчбек

Рис.3. Зависимость Сх от числа Re для модели 3 универсал
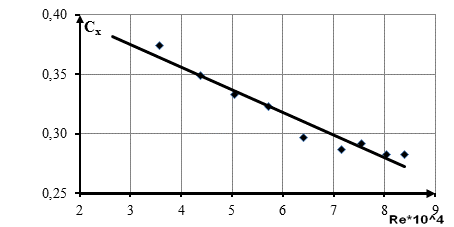
Рис.4. Зависимость Сх от числа Re для модели 1 седан
Из представленных графиков видно, что при увеличении числа Рейнольдса коэффициент аэродинамического сопротивления уменьшается, что даёт сделать вывод о приближении к зоне автомодельности. Недостижение этой зоны обусловлено рабочими характеристиками используемой при проведении эксперимента аэродинамической трубы, а именно – невозможностью компенсировать уменьшение размеров модели скоростью потока или свойствами газа, используемого при продувании.
Исследования выполнены при финансовой поддержке Министерства образования и науки РФ в рамках проекта по договору № 02.G25.31.0006 от 12.02.2013 г. (постановление Правительства Российской Федерации от 9 апреля 2010 года №218).
Рецензенты:
Петрухин Н.С., д.ф.-м.н., ординарный профессор Национального исследовательского университета «Высшая школа экономики», г. Нижний Новгород.
Карпухин В.Б., д.ф.-м.н., профессор кафедры «Высшая и прикладная математика» Российской открытой академии транспорта Московского государственного университета путей сообщения, г. Москва.



