Введение. Известно [2], [3], что экономика описывается динамической моделью фон Неймана при выполнении следующих условий: постоянство масштаба; возможность воспроизводства в любых количествах первичного фактора производства; соответствие уровня заработной платы уровню прожиточного минимума; инвестирование всего полученного дохода в пределах рассматриваемой экономики и т.д. Особый интерес здесь вызывают требования к производственному процессу. Целью процесса является преобразование уровней запасов некоторых продуктов, имеющихся к началу периода, в некоторые другие уровни запасов к концу этого периода. Для достижения этой цели основные процессы экономики можно комбинировать произвольным образом, добиваясь тем самым повышения эффективности процессов [4]. Это свойство в экономической теории обычно принимается без ограничений, хотя понятно, что в действительности оно должно часто нарушаться. Так происходит и в силу причин технологического характера (например, развитие двух влияющих друг на друга отраслей), и в силу политического устройства экономики (например, решение управляющего органа о приоритетном развитии какой-нибудь отрасли), и в силу, наконец, причин экономического характера (например, влияние отраслей друг на друга в силу действия различных конкурентных сил). Поэтому в исследованиях подобного рода естественно дополнительно накладывать или допускать условия, связанные с ограничениями пропорций основных отраслей экономики. Исследованию сформулированной проблемы и посвящена данная работа. При этом требования к пропорциям между процессами накладываются в виде принадлежности интенсивностей отраслей некоторому конусу. В работе устанавливается, что если определенным образом модифицировать понятие равновесия, то можно доказать, что оно существует и в таких условиях и, кроме того, при этом сохраняются известные свойства характеристик рассматриваемых экономик.

Модель экономики. Напомним сначала основные предположения, используемые в динамических моделях неймановского типа. Рассмотрим экономику (производство), описываемую парой , где - пространство товаров, - множество производственных процессов. Пусть имеющиеся в производстве типов продуктов-затрат с помощью технологических процессов превращаются в типов продуктов-выпусков. Тогда представляет собой неотрицательный ортант -мерного векторного пространства . Множество состоит из линейных неотрицательных комбинаций базисных процессов , функционирование которых описывается парой векторов из множества : . Это значит, что процесс при единичной интенсивности своей работы затрачивает набор продуктов и производит набор товаров , где - количества продукта с номером ,. По своему смыслу векторы .

Таким образом, , где линейные операторы и задаются матрицами затрат и выпусков , которые определяются равенствами

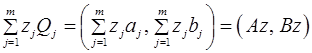, (1)

причем . Компоненты векторов называют интенсивностями, с которыми базисные процессы участвуют в производственном процессе . Будем считать, что вектор интенсивностей принадлежит некоторому замкнутому выпуклому конусу . Пусть также внутренность конуса не является пустым множеством.

Будем говорить (ср. [3]), что рассматриваемая модификация модели фон Неймана находится в состоянии динамического равновесия, описываемого параметрами , где - положительные числа, , если выполнены следующие две группы условий.

.

. Существует по крайней мере одно , с которым выполняется неравенство .

Здесь операторы определены в (1).

Содержательный смысл параметров заключается в следующем: в состоянии динамического равновесия производство всех продуктов остается в неизменной пропорции, хотя общий объем растет в геометрической прогрессии со знаменателем . Цены же на продукты остаются также в неизменной пропорции, но они должны падать также в геометрической прогрессии со знаменателем . Пропорции, в которых производятся продукты, определяются вектором , а пропорции цен – вектором цен . Отметим здесь также то, что по сравнению с обычной моделью фон Неймана правило нулевого дохода может здесь не выполнятся, требуется (условие 2) его выполнение не глобально в каждой отрасли, а по крайней мере в одной.

Известно, что фон Нейман [6] доказал существование динамического равновесия при определенных условиях на матрицы . Затем эти условия модифицировались различными авторами (см. [3]). С экономической точки зрения самыми подходящими требованиями здесь являются [5] условие неотрицательности матриц и и отсутствие в этих матрицах нулевых строк и нулевых столбцов соответственно. В настоящей работе также предполагается выполнение названных свойств у матриц и .

Итак, требования к рассматриваемой в данной статье экономике сформулированы. Докажем при таких условиях существование равновесия.

Существование равновесия. Изучим подробнее строение технологического множества . Прежде всего заметим, что множества , являются выпуклыми конусами в силу линейности операторов .

Для того, чтобы сформулировать следующие свойства множества , приведем модификации некоторых известных понятий [3]. Технологическим темпом роста модели экономики на луче , называется функция . Число называется технологическим темпом роста модели Неймана. Процесс является оптимальным, если .

Говорят [3], что продукт перепроизводится процессом , если .

Лемма 1. Если какие-либо продукты перепроизводятся некоторыми оптимальными процессами, то существует оптимальный процесс, производящий сразу все такие продукты.

Доказательство. Отметим, что множество оптимальных процессов представляет собой выпуклое множество. В самом деле, если то есть то в силу выпуклости множеств и получим, что , и . Значит, откуда по определению .

Возьмем два оптимальных процесса , перепроизводящих продукты и . В силу выпуклости множества оптимальных процессов середина отрезка также является оптимальным процессом. Проверка того, что процесс перепроизводит продукты и , тривиальна. Итак, если два оптимальных процесса перепроизводят два продукта, утверждение леммы справедливо. В случае большего числа продуктов вышеприведенные рассуждения нужно повторять соответствующее число раз, последовательно объединяя оптимальные процессы. Лемма 1 доказана.

Пусть - проекция пространства на пространство . Определим проекцию равенством .

Лемма 2. Проекция множества является замкнутым выпуклым конусом.

Доказательство. Утверждение следует из линейности операторов и того, что множество есть конус.

Лемма 3. В приведенных условиях модели технологический темп роста удовлетворяет условиям и реализуется на некотором процессе .

Доказательство. Заметим сначала, что если существует, то оно больше нуля. В самом деле, воспользуемся не пустотой внутренности множества . Возьмем положительный вектор . Для процесса в силу положительности сумм строк матриц имеем ; отсюда вытекает .

Рассмотрим теперь функцию на неотрицательном ортанте . Она определена в каждой точке , так как в силу свойств оператора в таких точках . Также как обычно [1], можно показать, что эта функция ограничена и полунепрерывна сверху на . Отсюда следуют те же свойства для функции , рассматриваемой уже только на множестве . Значит, существует процесс такой, что . Лемма 3 доказана.

Из леммы 3 следует существование (по крайней мере одного) характеристического процесса для множества . Пусть

, (2)

где

Определим проекцию пространства на пространство : . В силу лемм 2,3 существует технологический темп роста рассматриваемой модели экономики, определяемый множеством , который будем обозначать .

Лемма 4. Имеет место равенство . Существует такой процесс , что , причем на множестве у процесса нет перепроизводства, то есть выполняется соотношение .

Доказательство леммы получается дословным повторением аналогичного утверждения из [1].

Нужные свойства технологического множества получены. Докажем существование динамического равновесия. Имеет место

Теорема 1. Пусть - технологический темп роста модели. Тогда существует решение системы условий , обладающее следующими свойствами:

, (3)

, (4)

, (5)

. (6)

Доказательство. По условиям теоремы в силу леммы 3 существует технологический темп модели число . Рассмотрим множество . Оно, очевидно, является замкнутым выпуклым конусом. Из леммы 4 следует, что множество может иметь с неотрицательным ортантом самое большее одну общую точку . Итак, к множеству , как к выпуклому и непересекающемуся с множеству, можно применить теорему отделимости [3]. По этой теореме получим, что в пространстве существует вектор , такой, что для всех векторов из множества . Обозначим через -мерный вектор, который образуется дополнением вектора нулями до размерности . Пусть также векторы, введенные равенствами (2) и образующие характеристический процесс, а , - соответствующий им вектор интенсивностей. Тогда

, ,

где произвольны. Отсюда следуют следующие соотношения:

Положим . Равенство (6) теперь вытекает из определения , а соотношение

позволяет говорить о справедливости условий (4), (5). Так как при

,

то в силу для всехне могут выполняться неравенства . Теорема доказана.

Отметим, что равновесие, существование которого доказано в теореме 1, удовлетворяет соотношению . В таких случаях [1] равновесие называют невырожденным. Кроме того, выполнение равенства говорит о существовании стационарных траекторий интенсивностей и цен: .

Выводы. Модель экономики неймановского типа, описанная выше, является естественным обобщением модели Неймана: обобщение заключается в том, что допускаются ограничения на интенсивности базовых производственных процессов. Последнее является важным ослаблением традиционно используемых в таких моделях требований к технологическим множествам. С точки зрения экономики новые условия позволяют допускать такие, например, эффекты, как наличие управляющего органа в экономике, который ограничивая интенсивности базовых процессов, добивается поставленных целей. Накладывая на матрицы выпуска и затрат фактически те же требования, что и ранее в модели Неймана, при определенных свойствах множества интенсивностей удалось показать, что динамическое невырожденное равновесие в такой модели существует, существуют также стационарные траектории интенсивностей и цен. Необходимо также отметить, что при достижении выше указанного равновесия может нарушаться правило нулевого дохода. Если это происходит, то не во всех сразу отраслях, а только лишь в некоторых.

Рецензенты:

Роговой А.А., д. ф.-м.н., профессор, зам директора Института механики сплошных сред уральского отделения Российской академии наук, г.Пермь.

Перский Ю.К., д.э.н., профессор, профессор кафедры «Менеджмент и маркетинг» Пермского национального исследовательского политехнического университета, г.Пермь.