Среди систем поддержки принятия управленческих решений особое место занимают системы, позволяющие осуществлять динамическое моделирование процессов.
В представленной работе рассматривается динамическая модель, в которой денежные ресурсы и финансовые потоки ресурсов в единицу времени являются скалярными векторами на входе и выходе операторных звеньев [4, 5]. Одним из результатов, полученных на основе данной модели, является уравнение динамики роста капитала (1):
![]() , (1)
, (1)
где ![]() – текущий капитал организации,
– текущий капитал организации, ![]() – начальный капитал организации,
– начальный капитал организации, ![]() – время оборачиваемости капитала организации,
– время оборачиваемости капитала организации, ![]() – коэффициент передачи, равный доле прибыли, направляемой на накопление капитала организации,
– коэффициент передачи, равный доле прибыли, направляемой на накопление капитала организации, ![]() – маржинальная рентабельность.
– маржинальная рентабельность.
Согласно уравнению (1) капитал во временных точках ![]() после замены экспоненты первыми двумя членами разложения в ряд Маклорена может быть вычислен по формуле
после замены экспоненты первыми двумя членами разложения в ряд Маклорена может быть вычислен по формуле
![]() . (2)
. (2)
Коэффициент прироста ![]() для капитала, вычисляемого по формуле (2), равен
для капитала, вычисляемого по формуле (2), равен
![]() . (3)
. (3)
С экономической точки зрения логично принять гипотезу о том, что доля капитализируемой прибыли уменьшается пропорционально росту капитала, имея некоторый потолок роста ![]() , т.е.
, т.е.
![]() . (4)
. (4)
Подставив (4) в правую часть (3), имеем
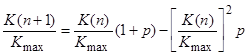 . (5)
. (5)
Введем новую переменную ![]() , тогда уравнение (5) можно записать в следующем виде:
, тогда уравнение (5) можно записать в следующем виде:
![]() . (6)
. (6)
Уравнение (6) идентично уравнению Ферхюльста [2].
Следовательно, динамика роста относительной величины ![]() капитала будет аналогична динамике численности популяции, описанной дискретной моделью Ферхюльста.
капитала будет аналогична динамике численности популяции, описанной дискретной моделью Ферхюльста.
Запишем дискретный аналог модели Ферхюльста
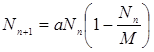 . (7)
. (7)
Для стационарного параметра ![]() логично, произведя в (7) замену переменной
логично, произведя в (7) замену переменной ![]() , получить более удобное для исследования уравнение
, получить более удобное для исследования уравнение
![]() , (8)
, (8)
где ![]() - отношение численности популяции к ее максимально возможному значению в периоде n,
- отношение численности популяции к ее максимально возможному значению в периоде n, ![]() [3].
[3].
Стоит отметить, что для поставленной в данной работе задачи исследования динамики изменения капитала согласно модели (7) в условиях неопределенности, т.е. при стохастическом изменении параметра ![]() , а, следовательно, и параметра
, а, следовательно, и параметра ![]() , вышерассмотренная замена переменных недопустима.
, вышерассмотренная замена переменных недопустима.
Возможность появления отрицательного значения переменной является существенным недостатком модели (6). Отрицательные значения являются следствием слишком большого значения величины капитала в предыдущем периоде (больше величины ![]() ), или слишком высокого коэффициента маржинальной рентабельности
), или слишком высокого коэффициента маржинальной рентабельности ![]() и начальном значении капитала около
и начальном значении капитала около ![]() . Однако, при
. Однако, при ![]() и при
и при ![]() величина капитала не может превзойти
величина капитала не может превзойти ![]() (а, соответственно, и оказаться отрицательной) ни при каких
(а, соответственно, и оказаться отрицательной) ни при каких ![]() , и модель (6) оказывается корректной.
, и модель (6) оказывается корректной.
При разных значениях параметра p наблюдаются существенно различные режимы динамики.
Характер динамики роста капитала будет зависеть от величины маржинальной рентабельности ![]() воспроизводственного процесса, так же как и динамика роста численности популяции от своего репродуктивного потенциала. По существу маржинальная рентабельность
воспроизводственного процесса, так же как и динамика роста численности популяции от своего репродуктивного потенциала. По существу маржинальная рентабельность ![]() является параметром роста для капитала в экономике. В зависимости от ее величины нелинейная динамика капитала будет претерпевать последовательно все качественные изменения, свойственные процессу для нелинейной динамики Ферхюльста. Поэтому естественно возникает задача исследования характера динамики при учете возможности изменчивости данного параметра. Постановка такой задачи в биологии уже встречалась в некоторых исследованиях. Например, получена оценка вероятности экстремального скачка в зависимости от характеристик случайных возмущений параметра, рассматривалась задача оптимизации промысла в модели динамики численности популяции с циклически меняющимся параметром [1].
является параметром роста для капитала в экономике. В зависимости от ее величины нелинейная динамика капитала будет претерпевать последовательно все качественные изменения, свойственные процессу для нелинейной динамики Ферхюльста. Поэтому естественно возникает задача исследования характера динамики при учете возможности изменчивости данного параметра. Постановка такой задачи в биологии уже встречалась в некоторых исследованиях. Например, получена оценка вероятности экстремального скачка в зависимости от характеристик случайных возмущений параметра, рассматривалась задача оптимизации промысла в модели динамики численности популяции с циклически меняющимся параметром [1].
В данной работе исследуется динамика роста капитала, описываемая уравнением (6), где параметр ![]() - случайная величина, плотность распределения которой:
- случайная величина, плотность распределения которой:
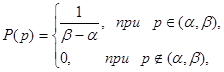
где ![]() .
.
Анализ имитации модели, проводимой в среде Delphi, позволяет сделать определенные выводы об особенностях динамики роста капитала и стратегиях регулирования этого процесса в условиях неопределенности.
Бифуркационные диаграммы, построенные для различных начальных значений и дисперсии капитала, иллюстрируют следующие результаты:
– в области устойчивости нетривиальной стационарной точки модели (6) ![]() , т.е. при
, т.е. при ![]() с течением времени значение капитала стремится к
с течением времени значение капитала стремится к ![]() , не зависимо от начального значения и дисперсии параметра,
, не зависимо от начального значения и дисперсии параметра,
– при ![]() значения капитала в стохастическом режиме, не зависимо от начального состояния, распределены вблизи значений капитала стационарного режима, повторяя форму и особенности бифуркационной диаграммы модели Ферхюльста с постоянным параметром.
значения капитала в стохастическом режиме, не зависимо от начального состояния, распределены вблизи значений капитала стационарного режима, повторяя форму и особенности бифуркационной диаграммы модели Ферхюльста с постоянным параметром.
График зависимости дисперсии капитала ![]() от среднего значения рентабельности
от среднего значения рентабельности ![]() при постоянной дисперсии
при постоянной дисперсии ![]() , свидетельствует о существенном влиянии начального капитала на рост дисперсии при значении
, свидетельствует о существенном влиянии начального капитала на рост дисперсии при значении ![]() близком к стационарной тривиальной точке модели Ферхюльста. Резкое увеличение скорости возрастания дисперсии, независимо от начального капитала, наблюдается при
близком к стационарной тривиальной точке модели Ферхюльста. Резкое увеличение скорости возрастания дисперсии, независимо от начального капитала, наблюдается при ![]() близком к 2 - точке бифуркации модели Ферхюльста, которая характеризуется появлением цикла длины 2.
близком к 2 - точке бифуркации модели Ферхюльста, которая характеризуется появлением цикла длины 2.
Линия тренда зависимости среднего значения ![]() капитала за n периодов от средней рентабельности
капитала за n периодов от средней рентабельности ![]() при постоянной дисперсии параметра
при постоянной дисперсии параметра ![]() демонстрирует возрастающую тенденцию в области устойчивости нетривиальной неподвижной точки уравнения Ферхюльста с постоянным параметром
демонстрирует возрастающую тенденцию в области устойчивости нетривиальной неподвижной точки уравнения Ферхюльста с постоянным параметром ![]() (т.е. при
(т.е. при ![]() ), а при
), а при ![]() наблюдается процесс убывания среднего значения капитала с достаточно высокой скоростью.
наблюдается процесс убывания среднего значения капитала с достаточно высокой скоростью.
Проведены исследования характера изменения величины капитала при наличии воздействия. Пользователем модели (лицом, принимающим решение) можно считать, например, крупных собственников или органы государственной власти. Модель роста капитала с учетом регулирования может быть использована при принятии решения по переброске капитала из одной сферы деятельности в другую.
Учитывая влияние воздействия, связь между величиной капитала в смежных периодах описывается уравнением
![]() . (9)
. (9)
Рассматриваются два типа оптимизационных задач. К первому типу относится задача реализации оптимальной стратегии эксплуатации. Такая стратегия предусматривает изъятие избыточного над некоторым фиксированным числом ![]() количества капитала, когда величина текущего капитала больше этого числа, и отказе от изъятия в противном случае.
количества капитала, когда величина текущего капитала больше этого числа, и отказе от изъятия в противном случае.
Величина изъятия в этом случае для равна
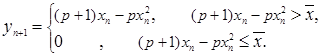
Задача оптимизации состоит в определении такого ![]() , при котором достигается максимум предела
, при котором достигается максимум предела ![]() .
.
Ко второму типу относится задача оптимизации изъятия капитала с величиной изъятия, пропорциональной текущему значению капитала, т.е. ![]() , причем доля изъятия
, причем доля изъятия ![]() может быть постоянна или переменна.
может быть постоянна или переменна.
Для модели Ферхюльста имеем соответственно
![]() . (10)
. (10)
Задача оптимизации состоит в поиске такого ![]() , при котором достигается максимум предела
, при котором достигается максимум предела 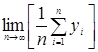 .
.
Для равновесного режима (![]() ) формула (10) примет вид
) формула (10) примет вид
![]() (11)
(11)
или
![]() . (12)
. (12)
Очевидно, что величина изъятия для первого типа задачи оптимизации при равновесном режиме с ненулевым изъятием рассчитывается по формуле (12).
Максимальное значение функции (12), равное, ![]() достигается, когда равновесное значение капитала
достигается, когда равновесное значение капитала ![]() .
.
Оптимальная доля изъятия вычисляется по формуле ![]() .
.
Функция ![]() является возрастающей, ее максимум на отрезке
является возрастающей, ее максимум на отрезке ![]() достигается в точке
достигается в точке ![]() ,
, ![]() .
.
Оптимальное значение капитала для модели с неслучайным параметром является устойчивым. Действительно, используя теорему Лагранжа при изучении поведения последовательность отклонений ![]() от положения равновесия при достаточно малом
от положения равновесия при достаточно малом ![]() , получим
, получим ![]() .
.
Вычислим ![]() .
. ![]() . Отсюда
. Отсюда ![]() . Так как
. Так как ![]() , то в силу непрерывности
, то в силу непрерывности ![]() существует окрестность точки
существует окрестность точки ![]() , для которой
, для которой ![]() . При достаточно малых отклонениях от положения равновесия
. При достаточно малых отклонениях от положения равновесия ![]() и соответственно
и соответственно ![]() лежат в этой окрестности, поэтому
лежат в этой окрестности, поэтому ![]() . Следовательно
. Следовательно ![]() , и оптимальное значение капитала устойчиво.
, и оптимальное значение капитала устойчиво.
Бифуркационные диаграммы для модели роста капитала с оптимальным для случайного параметра изъятием иллюстрируют уменьшение разброса значений величины капитала при оптимальном воздействии по сравнению с величиной капитала без изъятия. Кроме того, с ростом ![]() не наблюдается роста дисперсии капитала, как это было при отсутствии воздействия или при неоптимальном воздействии.
не наблюдается роста дисперсии капитала, как это было при отсутствии воздействия или при неоптимальном воздействии.
С увеличением дисперсии маржинальной рентабельности происходит уменьшение оптимальной доли изъятия и величины изъятия. Изучая зависимости средней величины изъятия и среднего значения величины капитала от изымаемой доли, можно предположить, что увеличение дисперсии параметра приводит к необходимости уменьшать долю изъятия относительно оптимальной доли ![]() , соответствующей детерминированной модели. Осуществление воздействия без учета стохастического характера параметра
, соответствующей детерминированной модели. Осуществление воздействия без учета стохастического характера параметра ![]() с постоянной долей изъятия, оптимальной для соответствующего параметра
с постоянной долей изъятия, оптимальной для соответствующего параметра ![]() детерминированной модели, приводит к риску не только снижения величины изъятия, но и к обнулению капитала при достаточно больших значениях дисперсии параметра.
детерминированной модели, приводит к риску не только снижения величины изъятия, но и к обнулению капитала при достаточно больших значениях дисперсии параметра.
Сравнительный анализ средних величин изъятия при оптимальной стратегии (стратегия 2) и стратегии с постоянной долей изъятия (стратегия 1) позволяет сделать вывод об уменьшении средней величины изъятия для обеих стратегий с ростом дисперсии параметра. Кроме того, с увеличением дисперсии параметра наблюдается увеличение разницы между величинами изъятия для стратегии 1 и стратегии 2. С увеличением математического ожидания параметра эта разница уменьшается, т.е. величина изъятия при обеих стратегиях управления с ростом математического ожидания параметра стремится к оптимальной величине изъятия, соответствующей модели с постоянным параметром, равного математическому ожиданию случайной величины ![]() .
.
Заключение
В данной работе произведена численная реализация модели Ферхюльста со случайным параметром ![]() , характеризующим потенциальную скорость роста капитала и подчиненным равномерному закону распределения. На основании результатов численного эксперимента на ЭВМ получены некоторые закономерности изменения математического ожидания и дисперсии величины капитала в зависимости от числовых характеристик случайного параметра
, характеризующим потенциальную скорость роста капитала и подчиненным равномерному закону распределения. На основании результатов численного эксперимента на ЭВМ получены некоторые закономерности изменения математического ожидания и дисперсии величины капитала в зависимости от числовых характеристик случайного параметра ![]() . Рассмотрено влияние внешних колебаний на автоколебания системы. Сделан сравнительный анализ результатов регулирования капитала при двух стратегиях воздействия.
. Рассмотрено влияние внешних колебаний на автоколебания системы. Сделан сравнительный анализ результатов регулирования капитала при двух стратегиях воздействия.
На основании результатов эксперимента сделаны следующие выводы:
- при росте дисперсии параметра оптимальная доля изъятия капитала, а также величина изъятия уменьшаются;
- увеличение доли изъятия приводит к уменьшению дисперсии величины капитала;
- величина изъятия при обеих стратегиях воздействия с ростом математического ожидания параметра стремится к оптимальной величине изъятия, соответствующего детерминированной модели с маржинальной рентабельностью, равной мат. ожиданию случайной величины
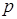 ;
; - оптимальное изъятие приводит к уменьшению разброса значений капитала;
- с ростом мат. ожидания параметра не наблюдается рост дисперсии капитала, как это было в отсутствие регулирования или при неоптимальном изъятии.
Сделанные выводы имеют определенный экономический интерес и могут быть использованы при управлении динамикой капитала, описываемой рассмотренной моделью.
Рецензенты:
Ембулаев В.Н., д.э.н., д-р транспорта, профессор, профессор кафедры математики и моделирования, ФГБОУ «Владивостокский государственный университет экономики и сервиса», г.Владивосток.
Мазелис Л.С., д.э.н., директор института информатики, инноваций и бизнес-систем, заведующий кафедрой математики и моделирования, ФГБОУ «Владивостокский государственный университет экономики и сервиса», г.Владивосток.



