Материалы и методика эксперимента
В настоящей работе объектом исследования был выбран алюминиевый сплав АМг6. Структурно-фазовое состояние материала в состоянии поставки исследовалось с использованием рентгеновского дифрактометра SHIMADZU XRD-6000. Сплав АМг6 имел следующий химический состав: Mg – 6,124%, Mn – 5,977%, Fe – 0,351%, Si – 0,310%, Zn – 0,203%, Ti – 0,0843%, Cu – 0,086%, Al – остальное.
Испытания образцов проката сплава АМг6 при одноосном растяжении и продавливании проводились на сервогидравлическом испытательном стенде Instron VHS 40/50-20 в соответствии с ГОСТ 1497-84, ГОСТ 10510-80, стандартами ASTM E643 - 09 и [1; 2; 6; 7].
Результаты и их обсуждение
На рис. 1а показаны диаграммы истинное напряжение – истинная деформация (линии 1-3) для сплава АМг6, полученные при одноосном растяжении при скоростях деформации - 0,001, 552, 485 с-1 соответственно. Диаграммы 1 и 2 получены для образцов листового проката сплава АМг6 с толщиной 1,5 мм в состоянии поставки. Диаграмма 3 получена для образцов со структурированными поверхностными слоями [5]. Диапазон равномерной пластической деформации 0 – δр отмечен на диаграммах квадратными символами. При деформациях, превышающих δр, в сечении образца начинает формироваться локальное сужение. При деформациях, превышающих значения в точках A, в образцах развиваются повреждения и формируется магистральная трещина. Таким образом, динамика разрушения в условиях одноосного нагружения отражается на участке АВ диаграмм высокоскоростного растяжения образцов.
а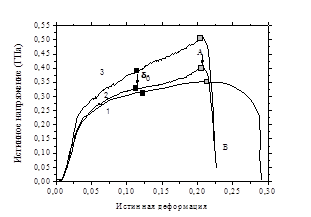 б
б 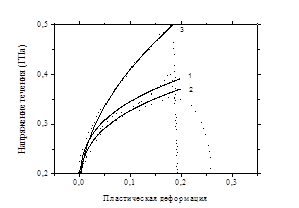
Рис. 1 - Диаграмма истинное напряжение – истинная деформация сплава АМг6 в состоянии поставки (1), (2) и со структурированным поверхностным слоем (3).
Полученные экспериментальные данные были использованы для оценки параметров модели, предназначенной для описания процессов пластического течения и разрушения сплавов с ГЦК-решеткой, к которым относится сплав АМг6 [5; 8; 10]. Численные значения коэффициентов модели уточнялись с использованием результатов компьютерного моделирования. Расчеты проведены с использованием оригинального программного комплекса и пакета Workbench ANSYS 13 AUTODYN. Расчеты выполнены с использованием метода дискретных элементов и метода сглаженных частиц (SPH). Определяющее уравнение было использовано в виде
![]() , (1)
, (1)
где σij , Sij - компоненты тензора и тензора девиатора эффективных напряжений, σij(m) , Sij(m) - компоненты тензора и тензора девиатора напряжений в конденсированной фазе, p – давление, δij – символ Кронекера, D – параметр поврежденности.
Уравнение состояния для давления использовалось в форме Ми-Грюнайзена
![]() , при
, при ![]() , (2)
, (2)
![]() при
при ![]() ,
,
где С1, С2, С3, K1, K2 – постоянные материала, С4 – коэффициент Грюнайзена, E – удельная внутренняя энергия, ![]() .
.
В расчетах использованы следующие значения параметров для сплава АМг6: ρ0 (m) =2,65 г/см3, С1= 70,5, С2= 165,9, С3=42,8, K1= 59,2 ГПа, K2=0, С4=1,99.
Для описания на микроскопическом уровне сопротивления деформированию легких сплавов использованы соотношения моделей [9; 10].
Напряжение пластического течения задано соотношением
![]() , (3)
, (3)
где A, B, C, n, m – константы материала,
![]() ,
, ![]() ,
, ![]() =1 с-1,
=1 с-1, ![]() - компоненты тензора скорости деформации,
- компоненты тензора скорости деформации,
![]() ,
, ![]() - компоненты тензора скорости пластической деформации,
- компоненты тензора скорости пластической деформации,
![]() , T – температура, Tm – температура плавления.
, T – температура, Tm – температура плавления.
Уравнение (6) позволяет получить хорошее согласие расчетного напряжения течения с экспериментальными данными. Расчетные диаграммы и экспериментальные данные для листового проката АМг6 в состоянии поставки и с наноструктурированными поверхностными слоями показаны на рис. 1б. Линии 1 и 2 соответствуют расчетам для материала в состоянии поставки и скоростям деформации 552 и 0,001 с-1 соответственно. Расчеты выполнены при значениях параметров A = 155 МПа, B= 380 МПа, C=0,0041, n=0,32, m =2,51, Tm.=933 К. Линия 3 получена для пластин с наноструктурированными поверхностными слоями при скорости деформации 485 с-1. Расчеты выполнены при значениях параметров модели A = 155 МПа, B= 775 МПа, C=0,0041, n=0,5, m =2,51, Tm.=933К.
Прогнозируемое напряжение течения оказывается несколько завышенным после начала локализации пластической деформации в образце (в зоне шейки).
Динамика разрушения, обусловленная структурными превращениями в сплаве АМг6 при развитии пластического течения, учитывалась в уравнении (4) с помощью параметра поврежденности D
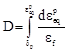 , (4)
, (4)
где εf – предельная степень пластической деформации до разрушения в условиях растяжения.
Величина εf рассматривалась как функция нормированной скорости деформации, температуры и параметра p/σeq, характеризующего сложное напряженное состояние
![]() (1- D4T*) (5)
(1- D4T*) (5)
где D1, D2, D3, D4 - постоянные материала.
Критерий разрушения в этом случае может быть записан в виде
D =1. (6)
Для оценки численных значений коэффициентов соотношения (5) проведено компьютерное моделирование условий экспериментов по высокоскоростному продавливанию пластин из АМг6 полусферическим индентером.
Испытания на динамическое продавливание образцов сплава АМг6 проводилось с применением полусферического индентера диаметром 20 мм в диапазоне скоростей от 0,01 до 15 м/с.
Схема испытания на динамическое продавливание показана на рисунке 2а. Образец в форме диска диаметром d мм и толщиной h обозначен - 1, пуансон - 2, нижняя и верхняя части опорной матрицы – 3 и 4 соответственно. Испытания проводились на дисках из сплава АМг6 толщиной 1,5 мм и диаметром 60 мм. Пуансон имел радиус R= 10 мм, а D=42 мм.
а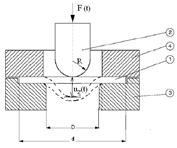 б
б 
Рис. 2 – Схема нагружения образца на динамическое продавливание
Приспособление для испытания на динамическое продавливание к сервогидравлическому испытательному стенду Instron VHS 40/50-20 показано на рис. 2б. Жесткость рамы испытательного стенда обеспечивала проведение испытаний при скорости индентера от 1 до 20 м/с. Регистрация усилия продавливания F(t) выполнялась с помощью сертифицированных пьезометрических измерительных головок Кистлера. Датчики калибровались для нагрузки 50 кН, допускали максимальную нагрузку 60 кН и максимальную перегрузку 72 кН. Точность измерения нагрузки составляет 0,25% в диапазоне от 1 до 100% номинальной мощность датчика. Усилитель датчика Кистлера имеет частотный диапазон 0-200 кГц. Точность измерения смещений u(t) поверхности контакта пуансона и образца обеспечивается калибровкой датчиков перемещений.
При проведении испытаний на универсальном испытательном стенде INSTRON VHS-40/50-20 обеспечивается постоянная скорость продавливания образцов. Для испытания применялись образцы диаметром 60 мм и толщиной 1,5 мм. Образцы вырезались механическим способом из листового проката сплава АМг6. Поверхность образцов обрабатывалась методом интенсивной пластической поверхностной деформации [5]. В качестве смазки поверхности контакта образца и индентора применялось индустриальное масло.
Регистрируемые во времени значения максимального перемещения в области продавливания образца uz(t) и усилия продавливания F(t) могут быть преобразованы в диаграмму F(uz) усилие – максимальное перемещение образца в направлении продавливания. Диаграммы изменения усилий продавливания F(uz) от перемещения 1-5 для скоростей 10, 7,5, 5, 0,005, 0,005 м/с показаны на рис. 2а. Линии 1-4 получены для образцов листового проката сплава АМг6 в состоянии поставки толщиной 1,5 мм, а линия 5 соответствует деформации образца с наноструктурированными поверхностными слоями.
Восходящая ветвь диаграмм на рис. 2 отражает закономерности неупругой деформации. Информация о динамике разрушения сплава АМг6 в условиях высокоскоростного продавливания образца полусферическим пуансоном содержится в нисходящей ветви диаграмм. Развитие повреждений в пластине при продавливании полусферическим пуансоном происходит в условиях сложного напряженно деформированного состояния.
а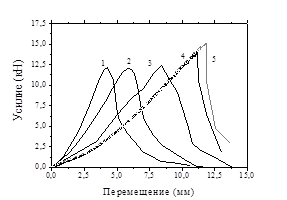 б
б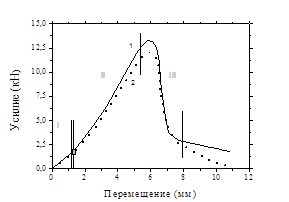
Рис. 3. Диаграммы продавливания пластин из сплава АМг6
На диаграмме F(uz) могут быть выделены характерные стадии (рис. 2б). Первая стадия соответствует упругой деформации пластины при продавливании. На второй стадии – в образце развиваются пластические деформации. Спад усилия деформирования на третьей стадии связан с образованием трещин и формированием зоны разрушения образца [3; 4].
Напряжение течения может быть определено по диаграмме продавливания с помощью соотношения [8]
![]() , (7)
, (7)
где P(t) –величина усилия продавливания, h – толщина, α – параметр материала.
Величина усилия P(t) в момент начала пластического течения определяется в точке пересечения диаграммы продавливания с прямой линией, параллельной оси усилия, отсекающей стадию I и смещенной на 0,1 h (рис. 2б) [6].
Отметим, что скорость продавливания влияет на динамику разрушения пластин и характер формирования трещин отрыва. Изменение характера разрушения с повышением скорости продавливания обусловлено развитием локализации пластической деформации в зоне интенсивного растяжения. Предельная деформация растяжения до разрушения εf может быть определена по измеренным значениям толщины на границе трещины с помощью соотношений [9]
![]() , (8)
, (8)
![]() , (9)
, (9)
где γ - параметр материала, hf – толщина образца на границе трещины, h0 – начальная толщина образца.
Соотношение (9) удобно применять для оценки предельной деформации до разрушения в условиях высокоскоростного продавливания. В этом случае зона разрушения имеет кольцевой характер (рис. 3в), не имеет вырывов, как при более низких скоростях продавливания (рис. 3б), и неоднородностей развития повреждений (рис. 3а).
При толщине образца на границе трещины 0,71 мм и начальной толщине пластины 1,47 мм предельная деформация εf при скорости 7,5 м/с оценивается равной 0,727 .
На рис. 4 показано расчетное поле интенсивности пластических деформаций при продавливании со скоростью 7,5 м/с. Расчетные значения εf лежат в пределах 0,733-0,799, что согласуется с оценками по формуле (9). Расчеты выполнены при значениях параметров D1=0,21, D2=0,4137, D3=1, D4=0.
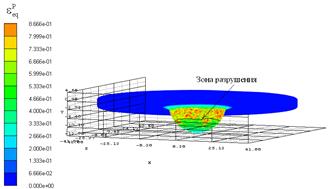
Рис. 4. Интенсивность пластической деформации в зоне продавливания
Расчетная зависимость силы продавливания от смещения центральной точки зоны контакта пластины и индентора при скорости продавливания 7,5 м/с показана на рис. 2б. Линия 1 - результаты расчета, линия 2 - экспериментальные данные. Отметим, что скорость деформации в зоне пластической вытяжки может варьироваться в пределах двух порядков.
Заключение
Предложенная модификация модели повреждаемой среды позволяет описывать закономерности пластического течения и разрушения сплава АМг6 в диапазоне скоростей деформации от 10-3 до 103 с-1. Полученные экспериментальные данные о механическом поведении сплава АМг6 в широком диапазоне скоростей нагружения, простом и сложном напряженном состоянии могут быть использованы при проектировании изделий и технологий их изготовления. Обнаружено, что наличие наноструктурированных поверхностных слоев на тонколистовом прокате приводит к повышению прочностных характеристик в диапазоне скоростей деформации от 10-3 до 103 с-1.
Автор благодарит профессора Скрипняка В.А., доцентов Козулина А.А. и Скрипняк Е.Г. за помощь в проведении экспериментальных исследований и обсуждении результатов.
Работа выполнена при финансовой поддержке Министерства образования и науки РФ (договор № 02.G25.31.0063) в рамках реализации Постановления Правительства РФ № 218, Соглашений 14.В37.21.0441 и 14.132.21.1700 и финансовой поддержке гранта Президента Российской Федерации МК-3066.2012.8.
Рецензенты:
Поляков В.В., д.ф.-м.н., профессор, заведующий кафедрой прикладной физики, электроники и информационной безопасности, декан физико-технического факультета, г. Барнаул.
Колубаев А.В., д.ф.-м.н., профессор, заведующий лабораторией физики упрочнения поверхности ИФПМ СО РАН, г. Томск.



