Введение
Одним из перспективных направлений термодинамического совершенствования и повышения системной эффективности комбинированных установок (КЭУ) является повышение параметров газа и пара перед газовой и паровой турбинами, усложнение схем с применением двух и трех уровней давления пара, комбинированная выработка электрической и тепловой энергии. Все это приводит к усложнению схем и снижению надежности работы ПГУ в системах теплоэнергоснабжения. Управление надежностью при создании энергетического оборудования с целью оптимизации конструктивных, технологических, схемных и эксплуатационных решений требует разработки методов и методик расчета единичных показателей надежности (ПН) элементов энергооборудования, главным образом безотказности. Модели надежности элементов энергооборудования и энергоустановок создаются на основе анализа их функционального назначения с учетом действительных факторов и условий работы, достоверности исходной информации, требуемой точности результата оценки надежности [4-6]. Детерминированные методы расчета ПН элементов энергооборудования, основанные на расчете коэффициентов запасов прочности и долговечности, не учитывают ряда реальных эксплуатационных факторов. В действительных условиях эксплуатации значения служебных характеристик металла (предел длительной прочности, предел усталости и др.) и действующих (растягивающих, изгибных, кручения, термических и др.) напряжений носят случайный характер из-за случайных нарушений стационарных режимов работы и отклонений характерных размеров элементов вследствие производственных, технологических и эксплуатационных факторов [3]. Поэтому расчет ПН элементов энергооборудования КЭУ должен базироваться на основе вероятностных методов, позволяющих учесть статистическое рассеяние характеристик прочности и нагруженности с использованием теории случайных величин и случайных функций.
Основные методические положения
Надёжность элементов оборудования КЭУ определяется:
- термонапряжённым состоянием металла элемента, температурный режим которого зависит от параметров рабочих тел, конструктивных особенностей, конструкционных материалов, режимов эксплуатации и ряда других факторов;
- в отдельных зонах элементов возникают пульсации температур, вызванные особенностями термодинамических процессов и нестационарностью расходов, давлений и температур рабочих тел. Причиной пульсаций температуры стенки труб, например, котлов-утилизаторов (КУ) КЭУ является изменение локальных коэффициентов теплоотдачи из-за высыхания микроплёнки жидкости на внутренней образующей труб испарительной поверхности. Пульсации температур вызывают соответствующие пульсации термических напряжений, которые, суммируясь со стационарными напряжениями, снижают надёжность КУ. Так как пульсации температур и напряжений носят случайный характер, а служебные характеристики материалов имеют статистическую природу, то расчёт показателей надёжности должен базироваться на использовании вероятностных подходов.
В соответствии с феноменологическим подходом к расчету надежности элементов энергооборудования [1] в основу математической модели расчета одного из важнейших единичных показателей надёжности элементов энергооборудования КЭУ, безотказности, положено следующее:
- действующие напряжения являются случайными величинами, разброс которых относительно математического ожидания определяется глобальными и локальными факторами. Глобальные неопределённости вызваны местными условиями и связаны с уменьшением, например, толщин стенки из-за технологических факторов, эрозией, коррозией и т.д. Все локальные неопределённости статистически независимы, поэтому для получения общего закона распределения случайных величин напряжений могут быть использованы свёртки дифференциальных функций;
- служебные характеристики применяемых материалов (предел длительной прочности и предел выносливости) являются случайными величинами, распределёнными по нормальному или логарифмически нормальному законам;
- оценка безотказности проводится из условия определения вероятности не превышения действующих напряжений над предельными значениями. Для определения этого условия используются свёртки дифференциальных функций распределения действующих напряжений и их предельных значений.
В соответствии с этим под безотказностью элемента следует понимать вероятность не превышения величины действующих напряжений 
прочности 
, то есть попадания случайной функции работоспособности (ФР) Z(t)= X(t)-Y(t) в область положительных значений. Значения аргументов функции X(t) и Y(t) в общем случае определяются их номинальными значениями 
и 
, а также постоянными 
и 
и переменными во времени 
и 
отклонениями. Если в элементе энергооборудования выделено 
участков или модулей, а безотказность каждого из них характеризуется 
ФР, то условие безотказности запишется в виде
, (1)
где k-количество анализируемых участков.
Таким образом, функция работоспособности 
является случайной функцией, колеблющейся около некоторого случайного стационарного уровня 
, положение которого определяется постоянными во времени отклонениями аргументов и от математического ожидания 
, рассчитываемого по номинальным значениям и .
Случайные колебания ФР около определяются только стационарными случайными функциями изменения расхода 
, давления 
, температуры 
и описываются законом
, (2)
где 
, 
, 
- средние квадратические отклонения ФР из-за переменных во времени локальных и глобальных отклонений.
В общем случае, когда несколько ФР определяют безотказность, то есть при 
, вероятность безотказной работы запишется в виде
. (3)
Если ФР независимы, то
. (4)
Величину 
определим по формуле
, (5)
где величина 
характеризует вероятность того, что случайная величина действующего напряжения не превысит допустимых значений в момент времени t, а величина 
соответствует вероятности отсутствия выброса случайной ФР в отрицательную область значений в течение времени t. Средняя частота выброса ФР в область 
в соответствии с [5] равна
, (6)
где 
- среднее квадратическое отклонение скорости изменения ФР , определяемое по автокорреляционной функции случайного процесса [5].
Для расчёта первого сомножителя в формуле (5) представим стационарные напряжения на любом выделенном участке элемента случайной величиной с математическим ожиданием 
и дисперсией D. Дисперсия стационарных напряжений D может быть оценена по коэффициенту вариации 
,определяемому как 
, значение которого находится в пределах 0,05…0,15 [7] .
Вероятность того, что для m - го выделенного участка элемента (опуская индекс m) действующие напряжения 
превысят предельные 
, то есть 
, определится как (см. рис.1)
, (7)
где 
- совместная дифференциальная функция распределения вероятностей приведённых напряжений и длительной прочности.
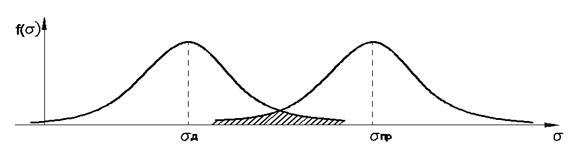
Рис.1 Дифференциальные функции распределения σд и σпр
Так как условие работоспособности участка элемента имеет вид 
, то используя его для определения областей интегрирования (7), получим
, (8)
В случае, если величины 
и 
распределены по нормальным законам, вероятность безотказной работы рассчитывается по формуле
, (9)
где 
- функция Лапласа, определяемая по [1]; 
- соответственно, математические ожидания и дисперсии действующих стационарных и предельных напряжений за период времени t.
Пользуясь квантилем функции нормального распределения uр и коэффициентом запаса, рассчитываемым как 
, получим
, (10)
где 
,
- соответственно, коэффициенты вариации действующих напряжений и допустимых значений.
Решение (9) получено при условии, что случайные величины действующих напряжений 
и их предельных значений 
распределены по нормальному закону с плотностью вероятности
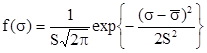, (11)
где 
,
- соответственно действующее (допустимое) напряжение, математическое ожидание случайной величины σ; S – среднее квадратическое отклонение случайной величины σ.
Использование нормального закона распределения случайных величин и предполагает интегрирование совместной функции их распределения (8) в пределах от -∞ до +∞. Вместе с тем, значения и не могут принимать отрицательные значения. Это означает, что в действительности необходимо использовать усеченное слева нормальное распределение. В этом случае плотность усеченного нормального распределения 
. Здесь нормирующий множитель с определяется из условия
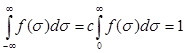. (12)
Отсюда величина с определяется как
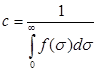(13)
Несложный анализ (13) показывает, что при отношении 
, величина с =1.
С использование разработанных методических положений проведены расчетно-теоретические исследования по определению влияния величины Кз и дисперсий случайных величин действующих и предельных напряжения на величину вероятности отказа элемента. На рис.2 показано изменение вероятности отказа q=(1-P) элемента в зависимости от величины коэффициента запаса Кз и дисперсии действующих напряжений и их предельных значений. Из рисунка следует, что величина Кз оказывает определяющее влия-
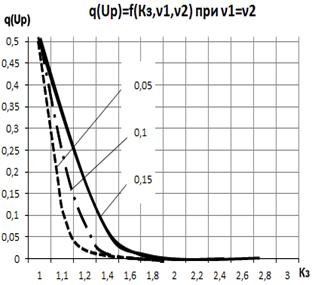
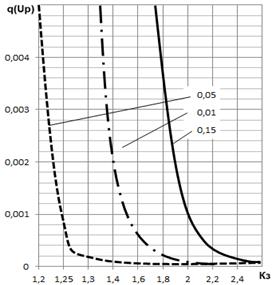
Рис.2 Влияние коэффициента запаса Кз на вероятность отказа элемента
ние на значения q. В связи с тем, что значения действующих напряжений зависят от большого числа факторов, то значения дисперсии действующих напряжений D(σд) существенно выше, чем величина D(σпр). Из рис.2 следует, что, например, при значении Кз=1,8 увеличение величины коэффициента вариации 
от 0,05 до 0,15 приводит к росту величины q на порядок. Это свидетельствует о необходимости тщательного обоснования величины .
Таким образом, определенные по представленной методике значения вероятностей отказа элемента энергооборудования определяются значениями коэффициента запаса Кз, законами и параметрами дифференциальных функций распределения случайных величин действующих напряжений и их предельных значений.
Реальные условия эксплуатации энергетических установок характеризуются переменными режимами работы с разным уровнем действующих напряжений, зависящих от уровня генерируемой мощности, давлений, температур, расходов рабочих тел и т.д. Указанные факторы определяют необходимость учета работы элементов энергооборудования на различных нагрузках, т.е. эквивалентирования режимов работы [2].
В основу эквивалентности режимов работы элементов КЭУ положено условие равновероятности отказа элемента в произвольном и эквивалентом режимах работы. Методика эквивалентирования иллюстрируется рисунком 3.
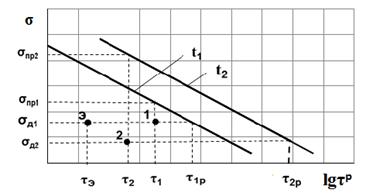
Рис.3 К эквивалентированию режимов работы элемента
Пусть режимы 1 и 2 работы элемента характеризуются значениями действующих напряжений 
и 
, температурами t1 и t2 и длительностью работы на этих режимах 
и 
.
Для приведения режима работы 2 к режиму 1 необходимо определить такой эквивалентный режим, который бы характеризовался действующим напряжением σд1, температурой металла t1 и эквивалентным временем τэ при условии равновероятности отказав произвольном и эквивалентом режимах. Это условие может быть записано в виде
(14)
После несложных преобразований с использованием уравнения длительной прочности металла элемента, τэ определяется по формуле
, (15)
где A,m – постоянные коэффициенты, зависящие от материала.
Если элемент работает на j=1,s уровнях нагрузки с длительностью работы τj , то время работы, приведенное к номинальному режиму работы 1 τпр (см. рис.3) определится как
. (16)
Используя полученное значение приведенного времени работы τпр и зависимости (9) позволяет рассчитать вероятность безотказной работы элемента с учетом режимов работы КЭУ в системе энергоснабжения.
Заключение
1. Разработана вероятностная модель расчета безотказности элементов энергетического оборудования комбинированных теплоэнергетических установок, учитывающая режимы их работы в энергетических системах.
2. Установлено влияние параметров дифференциальных функций распределения случайных величин действующих напряжений и их допустимых значений на вероятность отказа элемента.
3. Разработанные методические положения могут быть использованы для расчета показателей надежности структурно-сложных комбинированных теплоэнергетических установок.
Работа выполнена при финансовой поддержке Минобрнауки РФ (ГК 14. 740.11.0107)
Рецензенты:
Хрусталев В.А., д.т.н., профессор кафедры «Тепловые и атомные электрические станции» ФГБОУ ВПО «Саратовский государственный технический университет имени Гагарина Ю.А.», г.Саратов.
Семенов Б.А., д.т.н., профессор, заведующий кафедрой «Промышленная теплотехника» ФГБОУ ВПО «Саратовский государственный технический университет имени Гагарина Ю.А.»Э. г.Саратов.