Введение. Известно, что периодическое воздействие на жидкость часто приводит к возникновению осредненного течения. Природа воздействия может быть различной: периодический расход жидкости в канале, колебания полости с неоднородно нагретой жидкостью, вибрации тел, помещенных в жидкость, периодическое внешнее течение и т.д. Имеется большое количество работ, в которых исследуются осредненные течения, возникающие в обычной жидкости. В то же время малоизученным остается вопрос о влиянии периодического воздействия на фильтрацию жидкости в насыщенной пористой среде. В теоретическом плане проблема интересна тем, что уравнение фильтрации имеет более простой вид по сравнению с уравнением Навье-Стокса, что повышает возможности аналитического исследования. Изучение фильтрации при наличии периодического расхода жидкости представляет интерес с точки зрения технических приложений, например, в нефтедобыче при решении задачи о более эффективной разработке месторождений.
В немногочисленных работах по этой проблеме рассматривались в основном простые модельные задачи, в которых определялись условия возникновения осредненного течения. Отметим работу [1], в которой изучалось одномерное установившееся движение вязкой несжимаемой жидкости в неоднородном пористом скелете при периодическом воздействии. Получено интегральное соотношение для расхода жидкости, которое затем усреднялось по времени. В результате показано, что наличие неоднородности пористости среды по пространству приводит к возникновению осредненного течения жидкости. Следует отметить, что эффект, исследованный в работе [1], получен для частного случая плоскопараллельного течения. В других ситуациях осредненное течение может реализоваться при иных условиях либо отсутствовать. К настоящему времени пока не предложены уравнения осредненного течения в неоднородной пористой среде.
Целью данной работы является исследование вторичных течений жидкости, обусловленных периодическим расходом жидкости в каналах, заполненных насыщенной пористой средой.
Уравнения фильтрации при наличии периодического воздействия. Рассмотрим движение вязкой несжимаемой жидкости в канале, заполненном пористым материалом, физические свойства которого, в частности, коэффициент пористости 
, неоднородны по пространству. Движение жидкости в канале возникает под воздействием перепада давления на входе и выходе канала. На входе канала задан переменный расход жидкости через границу, зависящий от времени по гармоническому закону с частотой Ω и амплитудой скорости 
.
Уравнения, описывающие фильтрацию жидкости, представляют собой уточненную для случая неоднородной среды форму уравнения Форцгеймера и имеют вид (см. [4]):
(1)
где 
– скорость фильтрации, ν,
– кинематическая вязкость и плотность жидкости, 
, e – проницаемость и просветность пористой среды. Часто пытаются связать просветность с коэффициентом пористости. Так, с помощью гранулярной модели С. Слихтером установлено 
(см. [4]). Однако во многих других исследованиях считается, что просветность по величине равна пористости. Поэтому в дальнейшем полагаем 
.
Граничные условия сформулируем на твердой стенке Г для нормальной к границе компоненты скорости, на входе (in) и выходе (out) канала – для давления и скорости
, (2)
В дальнейшем нас будет интересовать случай, когда внешнее периодическое воздействие имеет высокую частоту по сравнению с гидродинамическими временами, что позволяет применить процедуру осреднения к системе (1).
Для получения осредненных уравнений представим скорость, температуру и давление в виде суммы усредненных 
и пульсационных 
компонент. Выделяя в уравнениях (1) пульсационные компоненты и, оставляя в них главные по амплитуде слагаемые, получим систему
Решения можно записать в виде 
. Уравнение для амплитуды пульсационной скорости имеет вид 
. Удобно изменить масштаб переменной 
, выделив из нее множитель 
В результате нормировки поле становится вещественным, так как поле 
вещественно вследствие дивергентности .
Уравнения для усредненных величин выводятся с использованием процедуры осреднения по времени системы уравнений (1). В уравнении фильтрации жидкости не учитывается слагаемое с ускорением ввиду его малости. Среднее от последних двух слагаемых в правой части вычисляется следующим образом
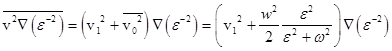
где 
и черта над выражением означает осреднение по времени. Опустим члены, нелинейные по скорости фильтрации 
, ввиду их малости: предполагаем, что осредненная скорость мала по сравнению с амплитудой пульсационной компоненты скорости 
. В результате получим систему
(3)
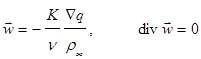. (4)
Уравнения (3)-(4) описывают осредненное течение, возникающее на фоне осциллирующего движения. Вторичное движение возникает под действием вибрационной силы, которая представлена в уравнениях слагаемым с градиентом пористости.
Перейдем к безразмерным переменным. Обозначим характерный размер канала (например, его длину) L. Выберем в качестве единиц измерения расстояния, скорости, давления, а также пульсационных компонент скорости и давления соответственно 
. Опустим индекс '1' у величины 
и переобозначим 
в 
. Уравнения фильтрации примут следующий вид
(5)
(6)
Граничные условия в безразмерных переменных имеют вид
. (7)
Краевая задача (5)-(7) содержит два безразмерных параметра – число Рейнольдса и безразмерную частоту
. (8)
Как правило, значения коэффициента проницаемости очень малы: 
м2. Следовательно, число Рейнольдса – малая величина, и сделанное ранее предположение, что осредненная скорость мала по сравнению со значениями переменной , верно.
Помимо указанного ограничения частоты снизу, связанного с применимостью метода осреднения, имеется также ограничение по частоте сверху, обусловленное использованием модели несжимаемой жидкости (длина звуковой волны должна быть намного больше характерного размера). Таким образом, частота вибрации должна удовлетворять неравенствам
, (9)
где c – скорость звука.
Плоскопараллельный фильтрационный поток. Рассмотрим одномерное движение жидкости – плоскопараллельный поток вдоль оси x декартовой системы координат. Он описывается уравнениями:
(10)
В уравнениях (10) штрих означает производную по координате 
. На входе 
и на выходе 
канала выполняются граничные условия (7). Решение данной задачи имеет вид
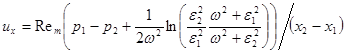(11)
Предположим, что рассматриваемый канал состоит из двух частей: прямолинейного участка насыщенной пористой среды между точками , и, замыкающего его, жидкого контура с низким сопротивлением. В этом случае внешний градиент давления отсутствует: 
. Тем не менее, если на входе и выходе канала пористость среды различна, возникает осредненное течение жидкости с постоянной скоростью, направленной в сторону увеличения пористости. Величина скорости зависит от проницаемости и градиента пористости среды, амплитуды и частоты периодического воздействия.
Приведем оценку величины осредненной скорости. Допустим канал длиной 10-1 м заполнен пористым материалом с постоянной проницаемостью 10-8 м2 и неоднородной пористостью, меняющейся по линейному закону от значения 1/3 на левой границе до значения 2/3 на правой границе. Пористый материал канала насыщен водой при температуре 25°С; амплитуда пульсации скорости на входе в канал 10-2 м/с, частота – 1 Гц. В этом случае модифицированное число Рейнольдса равно 10-3. Безразмерная осредненная скорость в отсутствие разности давлений 
, согласно выражению (11), равна 3,37·10-2, а размерная скорость – 3,37·10-4 м/с, что составляет примерно 3,4% от амплитуды периодического воздействия. Неравенства (9) дают следующие ограничения на частоту 
. Скорость осредненного течения пропорциональна проницаемости среды и убывает по квадратичному закону с ростом длины канала.
Заключение. Результаты работы свидетельствуют о существенном влиянии неоднородности характеристик пористой среды на ее гидродинамику. При наличии периодического движения жидкости в неоднородной пористой среде возникает вторичное течение, направленное в сторону увеличения пористости. Расчет этого течения можно выполнить с помощью уравнений, полученных в данной работе.
Рецензенты:
Тарунин Е.Л., д.ф.-м.н., профессор, Пермский государственный национальный исследовательский университет, г. Пермь.
Смородин Б.Л., д.ф.-м.н., профессор, Пермский государственный национальный исследовательский университет, г. Пермь.