Структурно-системные методы исследования объектов в процессе эволюции
Среди объектов природы и общества, с которыми имеет дело человек в научно-исследовательской и практической деятельности, преобладают «эволюционирующие» (или «динамические») объекты [4, 5]. Достаточно сложные из них являются открытыми системами [4], обменивающимися с окружающей средой энергией, информацией и веществом. Безусловно, открытыми системами являются организмы и их физиологические подсистемы. Высокая степени общности принципов системного подхода (в особенности, принципов структурно-системного исследования [7]) позволяет с успехом применять их как для изучения самых разнообразных открытых систем, так и для управления ими.
Предметом нашего специального интереса в рамках данной статьи является сердечно-сосудистая система человеческого организма, исследуемая структурно-системными методами. Для решения задач медицинской вычислительной диагностики в кардиологии предложен развитый авторами структурно-ориентированный подход [8-10], с успехом применявшийся для решения ряда актуальных задач неразрушающего контроля (НК), в особенности разработанные на его основе статистические теоретико-групповые методы решения обратных реконструктивных задач [8-10]. В силу сложности объекта открытая система является «многоуровневой» [4], а любое ее описание направленным и «селективным».
Наиболее существенной характеристикой открытой системы при ее взаимодействии со средой является сохранение ею целостности [4, 5], следовательно, и определенных структурных инвариантов [7], что дает основания выделить ее из окружения и рассматривать как квазинезависимый «кусок реальности». Меняясь, она остается сама собой, точнее изменения происходят в основном на уровне элементов [7] при сохранении ее «структурного ядра». Для открытой системы (как и для системы вообще) характерна ее принципиальная несводимость к сумме составляющих ее элементов и невыводимость из них свойств целого.
В рамках данной публикации предполагается «относительная устойчивость» системы и не рассматриваются катастрофические пути ее развития c разрушением «структурного ядра». Тем не менее, цели и задачи диагностики требуют распознавания «предкатастрофических» состояний, возникающих под действием различных факторов, приводящих к «сдвигу» определенных структурных инвариантов.
Диахрония и синхрония в исследовании эволюционных процессов
Существуют два подхода к изучению развивающихся систем – «диахронический» и «синхронический» [3]. В рамках диахронии рассматривают эволюционную последовательность развития явлений во времени, тогда как в рамках синхронии – их сосуществование в определенный момент времени. Такое противопоставление возникло в конце XIX-ого столетия после создания Ф. де Соссюром структурной лингвистики [3] и развития им «синхронического» подхода к языку в противовес эволюционному подходу в рамках сравнительно-исторического языкознания. В дальнейшем эти результаты в сильнейшей степени повлияли на становление и развитие структурных методов в науке.
Поскольку «синхронический» подход направлен на изучение системно-структурных и инвариантных свойств объектов, синхронию часто трактуют и как «вневременность». В математике, понятие «структура» применяется к множествам, природа элементов которых не определена. С этим тесно связана широкая распространенность в физико-математических науках (как, впрочем, и в системном анализе) реляционных моделей, отвлекающихся от «природных» свойств объектов (в частности, от их «элементной базы») и сосредоточенных на исследовании структурно-функциональных связей и отношений между элементами как в самом объекте, так и между объектами.
В структурном подходе «центр тяжести» исследования смещается с элементной (обычно материальной) основы объекта на формальные преобразования в нем. При этом исследуемый объект представляют как двухуровневую систему, разделяя в нем инвариантную структуру и субстрат, т.е. «подслой», нижний уровень, на котором, в основном, и осуществляются изменения в системе.
«Синхронический подход» – это «почти синоним» структурного подхода, однако употребляют его, когда хотят подчеркнуть присутствие эволюционных аспектов в исследуемом объекте. Субстратом для такого объекта является «уровень феноменов» или «круг явлений», связанный с этим объектом. Явления «эфемерны» и неустойчивы, тогда как структурное ядро объекта «относительно устойчиво».
Диахроническое и синхроническое (иначе говоря, эволюционное и структурное) описания объекта взаимно-дополнительны и, как таковые, друг другу не противоречат. Тем не менее, традиционным и предпочтительным описанием в науке остается все же структурное, которое обычно ассоциируется с точностью и объективностью. Это вполне объяснимо, поскольку знание нацелено в первую очередь на «неизменное» – на установление законов и на выявление инвариантов. В диахроническом подходе изучаются отношения, связывающие в «потоке явлений» элементы, следующие друг за другом во времени. Они не воспринимаются одним и тем же сознанием и не образуют системы. В синхроническом же подходе исследуют отношения, связывающие сосуществующие элементы. Они воспринимаются одним и тем же сознанием как целое и образуют систему. Можно сказать, что синхронический подход работает сразу со «всем списком» явлений, возможных в рамках данной теоретической модели.
В физико-математических науках «синхронический» подход ярко проявляется на уровне «законов сохранения» и «интегралов движения» физической системы, как и при выявлении ее структурных инвариантов при различных преобразованиях, описываемых на языке теории групп [7].
Разрабатываемый нами «теоретико-групповой статистический подход» к изучению и к диагностике «эволюционирующих» объектов, в особенности в связи с диагностическими задачами кардиологии, в основе своей – структурный. Направленность интереса в нем прежде всего на выявление пространственно-временных инвариантов в эволюционных процессах при предположении, что сами эти процессы динамически устойчивы. При этом акцент делается на выявление инвариантов, практически значимых для диагностики различных заболеваний.
Тем не менее, эволюционный (диахронический) подход в рамках этих исcледований не может быть «выброшен за борт». Во-первых, поскольку диагностически ценные инвариантные характеристики организма должны быть реконструированы из явлений, путем решения определенной обратной задачи. Во-вторых, диахронический подход становится актуальным при иcследовании воздействия различных внешних факторов на сердечно-сосудистую систему, также как и «внутренних» факторов, появляющихся в самой системе в процессе эволюции. При этом встает чуждая для синхронического подхода проблема анализа причинно-следственных связей, который осуществляется на основе принципа диссиметризации Кюри [9] в рамках теоретико-групповых статистических методов [8].
Обратные реконструктивные задачи для открытых систем
В рамках последовательного структурного подхода сама по себе теоретическая модель является объектом реконструкции и новым структурным целым.
Теоретические модели, которые создаются для описания поведения объектов в процессе эволюции, являются «динамическими». Иначе говоря, им присущи такие понятия как «время», «взаимодействие», «причина и действие» и пр. Отметим, что это лексикон, главным образом, диахронического подхода. Что касается самой теоретической модели, она является прерогативой синхронического подхода. Явления изменчивы, а заложенные в структуру теоретической модели законы, управляющие этими явлениями, константны, вневременны и «не имеют причины». Таким образом, при решении обратной задачи совершается переход от диахронического описания системы к синхроническому, а при решении прямой – от синхронического к диахроническому.
Обратная задача решается в рамках субъект-объектного единства. Решение требует гипотетических субъективных предположений AS и проверки их согласованности с объективными опытными данными AO об объекте исследования. По Лейбницу AO и AS – это «истины факта» и «истины разума» («vérité de fait» и «vérités de raison»). Принцип целостности при решении обратной задачи существенен. Предположение AS – это «интегрирующая идея» (организующее целое, которое субъект вносит в решение), без которой задача остается «нерешабельной» даже при всей полноте исходных данных, т.е. ее появление – не есть прерогатива «некорректных» задач, а характерно для всех, без исключения, обратных задач. В рамках теоретико-группового статистического подхода AS –это теоретико-групповые гипотезы об объекте исследования, которые проверяются статистическими методами.
Мультивариантность и направленность в решении обратных задач
В силу многоуровневости объекта исследования в его информационном образе объекта контроля может содержаться множество «смыслов» [8], в общем случае рассогласованных друг с другом. Решение обратной задачи РВД направлено на выявление какого-то определенного смысла. В зашумленном радиографическом изображении объекта могут быть выявлены разные «смысловые структуры» путем проверки теоретико-групповых статистических гипотез, причем основным формальным инструментом теоретико-групповой фильтрации является гипотетическая локальная группа Ли LS [8]. (Пример – распознавание и выявление локально-анизотропных образов на основе локальной группы SO (2) [8]). Данный метод легко обобщается на многоракурсные (т.е. томографические) задачи.
При переходе к «динамической ситуации» в информационном потоке (в серии изображений эволюционирующего объекта) конкретная «смысловая структура» появляется с характерным для нее периодом T. Все другие структуры (с другими несоизмеримыми периодами) будут в серии изображений с периодом T рассогласованы. В этой ситуации для выделенной структуры возникают дополнительные «ракурсы» и она может быть восстановлена с существенно большей степенью детализации, чем на основе лишь одного ракурса.
Из сказанного выше легко понять, что систему РВД для «динамического контроля» уместно проектировать как стробоскопическую, что вполне согласуется с концепцией теоретико-групповых реконструктивных методов. Как известно, стробирование определяется как выделение из последовательности сигналов полезного сигнала, отличающегося каким либо признаком. Таким образом, в технику стробирования уже на стадии регистрации данных заложена определенная предфильтрация. В соответствии с методологией стробоскопии предполагается, что в системе РВД информационный поток, идущий от «динамического» объекта контроля, регистрируется только в те моменты времени, когда на ее подсистему сбора данных подается cтробирующий сигнал. Во все остальные моменты регистрация данных блокирована.
В отличие от классических стробоскопов систему РВД, работающую в стробоскопическом режиме, будем представлять таким образом, что за промежуток времени между t = kT и t = (k + 1)T решается определенная обратная реконструктивная задача и ее решение «высвечивается» на регистрирующем приборе (что можно понимать и буквально, например, томограмма «динамического объекта» с заданной глубиной залегания высвечивается на экране монитора).
Стробоскопическая реконструктивная диагностика в фазовом времени
Поскольку реальные ритмы открытых систем неточны, классические стробоскопические методы неэффективны для их исследования. Методика стробоскопии в применении к неточным периодическим процессам может быть усовершенствована при более гибком подходе к понятию «время». Введем наряду с обычным «физическим» временем, для которого используется переменная t, еще фазовое время τ, характеризующее определенную фазу θ циклического процесса, таким образом, что осуществлено взаимно-однозначное соответствие между t и τ, т.е.
t = t (τ} и τ = τ (t), (1)
где (1) являются монотонными неубывающими функциями, при этом τ (T) = 2π , t (2π) = T, τ = 2π k + θ, где k - номер цикла и, θ = τ - 2π k и для диапазона изменения фазы имеем 0 ≤ θ ≤ 2π . Фазовое время и фаза равны по модулю сравнения 2π, т.е. τ = θ (mod 2π). Стробирующие сигналы на систему регистрации исходных данных будем теперь подавать также равномерно, как и в традиционной стробоскопии, но только в фазовом времени (с периодом Θ). В частности, удобно осуществлять стробирование таким образом, что стробирующие сигналы подаются в моменты τ фазового времени, соответствующие фиксированным фазам θ (с периодом Θ = 0, что равносильно Θ = 2π). При небольших отклонениях Δθ периода Θ от 2π будет наблюдаться медленная эволюция объекта контроля в фазовом времени с круговой частотой Δω = Δθ/2π, где направление эволюции определяется знаком Δθ. При Δθ = 0 объект «неподвижен».
Исходным пунктом для введения фазового времени является очевидное предположение о том, что близость состояний контролируемой системы (например, сердца) в одних и тех же фазах θ выше, чем в моменты физического времени t1 и t2, разделенные целым числом периодов m, т.е. при t1 - t2 = mT (по другому, в моменты времени, равные по модулю сравнения T). Произвольные состояния контролируемого объекта из класса, определяемого уравнением θ1 = θ2 (mod 2π) ближе друг другу, чем произвольные состояния из класса t1 = t2 (mod Т).
Традиционная стробоскопия работает с точными периодами и точным повторением состояний объекта за эти периоды. Здесь же речь идет о «неточной» или «обедненной» симметрии состояний для различных реализаций, соответствуюших фазе θ. Состояния с одной и той же фазой θ попарно связаны между собой отношением эквивалентности и объединяются в классы эквивалентности CLθ, для каждого из которых существует система признаков CHθ. В данном случае класс близких состояний CLθ определяется как класс сравнений θ1 = θ2 (mod 2π). Любая реализация может быть переведена в другую с той же фазой преобразованием подобия таким образом, что все признаки из CHθ сохраняются. Эти преобразования образуют транзитивную группу [6] Gθ, операторами которых являются всевозможные переходы от состояния ki к состоянию kj, где ki и kj из набора номеров реализаций ( k = 1,2, . …, K).
В истории науки можно найти прецеденты, напоминающие ввод «фазового времени» Так, А.Л.Чижевскому, изучавшему солнечно-земные связи и влияние солнечной активности на различные биологические и социальные процессы [6], приходилось сравнивать между собой разные реализации 11-летнего цикла солнечной активности. Он неточен. Нередко наблюдались реализации в 7 лет и в 17 лет. Для извлечения достоверных выводов из экспериментальных данных необходимо привести их к единому масштабу, т.е. по сути дела перейти к фазовому представлению цикла. Чижевский называл это «методом наложения эпох» [6].
Подобная «калибровка» данных смещает рассмотрение проблемы в сторону «синхронии», давая тем самым возможность исследовать эволюционирующие объекты в рамках методологии структурного подхода и на основе его формальной техники. Решающим шагом в этом направлении является установление изоморфизма между циклами. Конечно, осуществить это можно многими способами при сохранении последовательности фаз, что обеспечивается монотонностью преобразований (1).
Кардиограммно-управляемая реконструктивная медицинская диагностика
Законы преобразования (1) в применении к кардиологии не могут быть получены сразу на длительное количество циклов, поскольку сердце является достаточно капризным «механизмом». Признаки тахикардии или брадикардии могут проявиться неожиданно под действием самых различных факторов. Поэтому для предвычисления момента физического времени t для подачи стробирующего сигнала на систему регистрации согласно закону t = t (τ} на каждом цикле проводится коррекция (1) по принципу «предсказание-уточнение» с учетом результатов измерения параметров кардиограммы (прежде всего позиций зубцов) на нескольких предыдущих циклах.
Это неизбежно накладывает особые требования к качеству регистрируемой электрокардиограммы. Обычные электрокардиографы имеют чувствительность по уровню 20 мм, 10 мм, 5 мм / 1 мВ и достаточно узкий частотный диапазон от 0,05 Гц до 40-100/150 Гц в обычных электрокардиографах и от 0,05 до 250 Гц в электрокардиографах высокого разрешения, что не позволяет точно определить значения амплитудно-временных параметров зубцов электрокардиограммы. В [1] показано, что точное описание зубцов электрокардиограммы как по уровню, так и по времени, обеспечивает электрокардиограф на наноэлектродах, который имеет следующие технические характеристики:
- диапазон входных напряжений от ± 0,0002 мВ до ± 20 мВ (по ГОСТ 19867-89 от 0,03 мВ до 5 мВ);
- уровень внутренних шумов от пика до пика – от + 0,1 мкВ до – 0,1 мкВ (по ГОСТ 19867-89 менее 20 мкВ);
- диапазон частот – (0-20)/(0-40)/(0-75)/(0-100)(0-10000) Гц;
- частота квантования – 200/250/1000/2000/20000 Гц;
- число каналов – 1-3;
- число электродов – 3-7;
- передача ЭКГ на удаленный терминал при помощи накопления информации на встроенную в ЭКГ-аппарат флэш-памяти либо по прямому каналу связи с ПК при помощи порта USB.
Данный электрокардиограф позволяет измерить фрагменты электрокардиограммы, равные одному микровольту, менее одного микровольта либо нескольким микровольтам в расширенном частотном диапазоне от постоянного тока до 10000 Гц с разрешением по уровню 20 нВ.
В качестве примера приводим запись электрокардиограммы пациента П49 после перенесенного инфаркта (рис.1).
а) 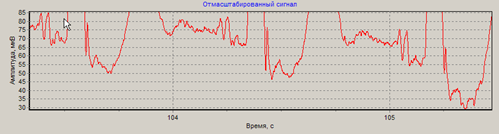
б) 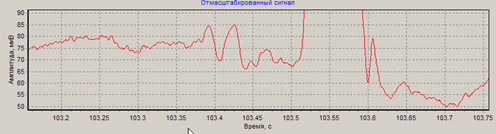
Рис. 1. Записи электрокардиограммы высокого разрешения:
а – низкоамплитудные зубцы P и U; б – фрагмент записи на 103 с.
Из рис.1а видно, что зубец Р имеет уровень, равный 15 мкВ, зубец U – 5 мкВ. На рис. 1б низкоамплитудные флуктуации составляют сотни нановольт.
На рис. 2 представлен график частоты сердечных сокращений (ЧСС) того же пациента, который подтверждает факт нестабильности периода кардиоцикла, который изменяется у данного пациента от 71 ударов в минуту до 74 ударов в минуту.
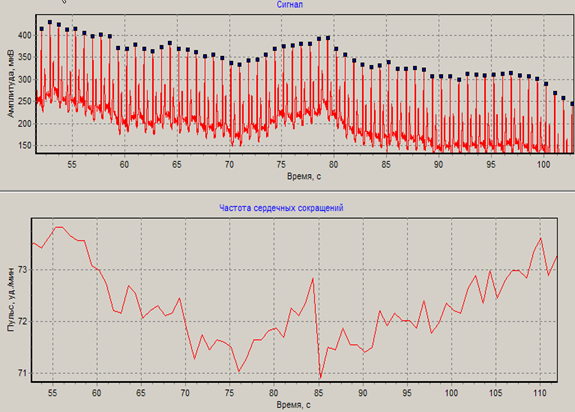
Рис.2. Частота сердечных сокращений пациента П49
Высокое разрешение при измерении электрокардиограмм в сочетании с их представлением в фазовом времени открывает новые возможности в исследовании сердечно-сосудистой системы. Прежде всего, это касается выявления и оценки тех ее характеристик, которые инвариантны относительно преобразований из группы Gθ.
Выражаясь проще, становится возможным выделение и изучение тех характеристик, которые общие для фазы θ во всех реализациях сердечных циклов. Такие задачи эффективно решаются в рамках теоретико-групповых статистических методов [8-10].
При этом доступная исследователю исходная информация очищается от «смысловых шумов» – от тех «неинвариантных свойств», которыми «зашумлены» отдельные реализации. Эта работа во многом похожа также на «разделение слоев» в «нелинейном томосинтезе» [8-10] и осуществляется на той же концептуальной основе. Однако в данном случае уместнее говорить о выделении «смысловых слоев», каждый из которых характеризуется своим параметром θ.
Подытоживая эти рассуждения, уместно сказать, что высокое разрешение при измерении электрокардиограмм в сочетании с их представлением в фазовом времени, как и в связи с развитием теоретико-группового статистического подхода к реконструкции объектов открывает путь для комплексного изучения проблем кардиологии математическими методами.
Решение реконструктивных задач для эволюционирующих объектов на основе теоретико-групповых статистических методов
Реконструктивные задачи для эволюционирующих объектов, решаемые в рамках структурного (теоретико-группового статистического) подхода, могут быть разделены на два класса:
- «квазистатические» или «чисто пространственные» задачи, каждая из которых решается для определенного момента фазового времени τ, т.е. зависимость решения от времени здесь только параметрическая;
- нетривиальные «динамические» задачи, в решениях которых выявляются пространственно-временные инварианты эволюционирующего объекта.
«Квазистатические» задачи
Что касается этого типа задач, на них с успехом переносится «математическая техника» теоретико-групповых статистических методов, развитых для решения задач НК [8-10]. Сюда входят как задачи томографии [10], так и реконструкции изображений [8]. В типичной ситуации решается серия статических задач для моментов времени τ = 2πk + θ при k = 1, 2, …, K при фиксированной фазе θ. Они решаются раздельно и связь состояний по параметру θ не учитывается. Тем не менее, такая серия решений дает уже много новой информации об объекте в состоянии с параметром θ, в частности, возможность сравнительного визуального анализа решений, выявления инвариантов и отклонения от них в отдельных решениях, а также прослеживания влияния разнообразных факторов на такие отклонения. На этом, в свою очередь, основывается разработка новых алгоритмов и программных инструментов для постобработки серии решений.
При τ = Δθ k + θ серия «квазистатических» решений позволяет отслеживать медленную эволюцию объекта вблизи состояния θ с круговой частотой Δω = Δθ/2π. Все соображения о сравнительном анализе решений и постобработке справедливы и в этом случае.
«Динамические» задачи
Изначальная внутренняя неустойчивость является «мотором» саморазвития любой открытой системы, в частности, организма. Важным аспектом такого развития является динамическая устойчивость – сохранение системой определенных динамических структурных инвариантов на определенном «значимом» участке ее эволюции, что дает право рассматривать ее как самоидентичный объект. В «динамических» задачах связь K состояний объекта по параметру θ учитывается с самого начала и серия (k = 1, 2, …, K) рассматривается как структурное целое.
Исследование внутренних динамических неустойчивостей сердечно-сосудистой системы принципиально важно для диагностики патологий в ней. Самая заметная из таких неустойчивостей, связанная с неточными ритмами сердцебиения, – «слабая», сама по себе не являющаяся индикатором каких-то заболеваний. Скорее, это эффективное средство адаптации к разнообразным воздействиям на организм (как внешним, так и возникающим внутри него). Для патологических неустойчивостей требуется ранняя диагностика, поскольку для них характерна тенденция к быстрому («нелинейному») развитию.
Типичными «динамическими» задачами являются установление «нормального» состояния для объекта контроля и выявление отклонений от него под воздействием разнообразных факторов. По сути дела, это задача математического описания гомеостазиса (т.е. поддержания постоянства существенных переменных организма), на основе теоретико-групповых статистических методов.
С позиций биологии и медицины единая норма здоровья это нечто трудноопределимое. Более корректным было бы говорить о разных «нормах» для разных контингентов людей, однако в рамках данной исследовательской программы интересы смещены даже не на это, а на разработку методов формализации «нормы» как структуры, описываемой своими структурными инвариантами.
Если речь идет об обычных «спокойных» состояниях организма, то в число инвариантных могут быть включены такие его характеристики как ЧСС, систолическое и диастолическое давление, систолический и минутный объем крови и др. При расширении набора состояний организма путем стрессовых воздействий на него набор инвариантных характеристик сузится. Важным классом «динамических» задач диагностики является также оценка времен релаксации организма после воздействий.
Простым примером такого фактора может быть стрессовая физическая нагрузка, когда ЧСС (явно неинвариантная величина) поднимается до 220 ударов в минуту и более. Для развития диагностических методов интересно сравнение серии рентгенограмм сердца в какой-то определенной точно фиксированной фазе с параметром θ за период, когда ЧСС спадает до нормы. В случае предельных (для данного организма) нагрузок становятся возможным уже и выявление некоторых небольших сдвигов в самих «инвариантных» характеристиках.
В рамках теоретико-группового статистического подхода [8,9] задача различения нормы и аномалии в объекте контроля сведена к задаче различения статистически значимой симметрии и диссимметрии в его информационном образе (серии рентгеновских проекций). Решение строится на основе проверки теоретико-групповой статистической гипотезы об инвариантности информационного образа относительно преобразований из гипотетической локальной группы Ли LS [8]. «Выдерживание» организмом инвариантных характеристик в пределах «нормы» – это нулевая гипотеза. Соответствующее определенной аномалии статистически значимое отклонение от инварианта – это альтернативная гипотеза. Понижение симметрии структуры (в частности, структуры, описываемой группой Gθ.), вызываемое этим фактором, оценивается на основе принципа диссимметризации П. Кюри [9], причем для количественной оценки понижения симметрии строятся статистические «меры различия» [8].
Подобно тому, как результат структурно-ориентированного НК может быть представлен в форме карты дефектности [9], строящейся на основе теоретико-групповых принципов, в медицинскую диагностику может быть введена «карта патологий», формирующаяся на тех же принципах. (Подчеркнем, что она дает «синхроническое» описание организма). Ее уместно строить не в трехмерном, а в каких-то других конфигурационных пространствах, отражая нарушения наиболее важных (с точки зрения установленной «нормы») структурно-функциональных связей организма и представляя, таким образом, своеобразный «структурно-функциональный портрет» пациента.
Результаты и выводы
Позитивный опыт, накопленный при решении ряда проблем неразрушающего контроля с применением статистических теоретико-групповых реконструктивных методов, позволил разработать аналогичные методы для решения задач реконструкции инвариантных характеристик эволюционирующих объектов, в первую очередь, для решения диагностических задач в кардиологии.
Наиболее значимыми результатами данной публикации являются следующие:
1. Развит структурный подход к объекту в процессе эволюции, как к открытой системе. Исследована сущность обратной реконструктивной задачи с позиций структурного подхода. Подробно обсуждены особенности обратных задач для открытых развивающихся систем.
2. Предложено и обосновано применение стробоскопических методов регистрации данных в системах вычислительной диагностики для реконструкции эволюционирующих объектов.
3. Решена проблема калибровки неточных ритмов эволюционирующих объектов и введено понятие фазового времени. Развиты методы стробоскопической реконструктивной диагностики в фазовом времени.
4. Предложены кардиограммно-управляемые системы реконструктивной медицинской диагностики. Обсуждены возможности их аппаратной реализации на основе электрокардиографа, позволяющего измерять фрагменты электрокардиограммы, равные одному микровольту, менее одного микровольта либо нескольким микровольтам в расширенном частотном диапазоне от постоянного тока до 10000 Гц с разрешением по уровню 20 нВ.
5. Рассмотрены основные типы «статических» и «динамических» задач при реконструкции инвариантных характеристик объектов в процессе эволюции. В рамках теоретико-групповых статистических методов обсуждены вопросы формализации «нормы» контроля и выявления аномалий как понижения симметрии фона под воздействием внешних факторов.
Потенциальная сфера приложений рассмотренных в данной работе математических методов реконструкции объектов в процессе эволюции представляется широкой, включая помимо медицинской диагностики также геофизику, астрофизику, оптимизацию управления в системе «человек-машина» и пр. К настоящему моменту решены основные теоретические вопросы, касающиеся разработки кардиограммно-управляемых рентгеновских систем для медицинской диагностики. Не вызывает сомнений, что достигнутые результаты могут быть перенесены на многие другие сферы приложения.
Работа выполнена при финансовой поддержке:
1)«Проведение фундаментальных исследований по выявлению изменений электрокардиографического сигнала нановольтового и микровольтового уровня с целью ранней диагностики сердечно-сосудистых заболеваний» по Госзаданию «Наука».
2)«Исследование искажений тонкой структуры (низкоамплитудных высокочастотных колебаний) биопотенциалов сердца и мозга, вносимых фильтрующими схемами медицинского диагностического оборудования; поиск путей устранения помех с сохранением тонкой структуры уровнем менее 1 мкВ в полосе частот 0 – 150 Гц» - проект № 12-08-00996 Российского фонда фундаментальных исследований.
Рецензенты:
Агафонников В.Ф., д.т.н., профессор кафедры конструирования узлов и деталей РЭС (КУДР) Томского университета систем управления и радиоэлектроники, г.Томск.
Светлаков А.А., д.т.н., профессор кафедры электронных средств автоматизации и управления Томского государственного университета систем управления и радиоэлектроники, г.Томск.



