Введение
В спортивной сфере, как и в любой другой области науки, перспективно применение методов математического компьютерного моделирования. Однако, ввиду плохой формализуемости знаний, а также большого количества факторов, влияющих на результат моделирования, качественные математические модели традиционными детерминированными методами в спортивной сфере построить достаточно трудно.
В последнее время для слабоструктурированных и плохо формализуемых предметных областей получает распространение сравнительно новый математический аппарат, называемый нейросетевыми технологиями. Нейрокомпьютерные и нейросетевые технологии являются одной из наиболее эффективных стратегий искусственного интеллекта. Предложенные в основополагающих работах У. Мак-Каллока, В. Питтса и Ф. Розенблатта [7; 8], нейронные сети реализуются по принципам построения и функционирования человеческого мозга. Они наследуют от своего прототипа – мозга его полезные свойства: способность извлечения знаний из статистических данных, способность обобщения их в виде закономерностей предметных областей, свойство интуиции [4; 6] как способность делать правильные заключения на неполной информации, строить прогнозы и вырабатывать управляющие воздействия в тех случаях, когда обычная логика оказывается бессильной. Как убедительно показывает наш собственный опыт [2-6], хорошо спроектированные и правильно обученные нейронные сети способны самостоятельно выявлять закономерности практически любых предметных областей и строить адекватные математические модели в промышленности, в экономике и бизнесе, в политологии и социологии, в криминалистике, в медицине, в экологии и энергосбережении, в исторических науках и др. По-видимому, не является исключением и спорт, в частности – фигурное катание.
Методика прогнозирования
При построении нейросетевой математической модели, предназначенной для прогнозирования победителя в мужском одиночном фигурном катании в 2014 году, было сформировано множество примеров, основанных на результатах предыдущих чемпионатов мира, чемпионатов Европы, а также Олимпиады-2010 в Ванкувере. Входные параметры модели, по которым оцениваются претенденты, взяты исходя из доступности информации о спортсменах в сети Интернет [1]: страна; возраст; рост; вес; начало занятия на коньках, (возраст участника, когда встал на коньки); шаги; вращения; прыжки; травмы; количество медалей до чемпионата; был ли мировой рекорд перед соревнованиями; и др. Выходной параметр модели кодировал результат выступления спортсмена – место в чемпионате.
Множество примеров из истории проведения чемпионатов мира, чемпионатов Европы и Олимпиады-2010 в Ванкувере было разбито на обучающее, использованное для обучения сети, и тестирующее, предназначенное для проверки ее прогностических свойств. Естественно, что примеры тестирующего множества при обучении сети не использовались.
Проектирование, оптимизация, обучение, тестирование нейронной сети и эксперименты над нейросетевой математической моделью выполнялись с помощью нейропакета [2]. Оптимальная структура нейронной сети представляла собой персептрон [3; 4], имеющий одиннадцать входных нейронов, один скрытый слой с четырьмя нейронами и один выходной нейрон.
В качестве активационных функций нейронов скрытого слоя и выходного нейрона использовались сигмоидные функции (рисунок 2), так что вычисления каждого ![]() -го нейрона осуществлялись с помощью формул:
-го нейрона осуществлялись с помощью формул:
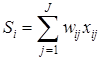 , (1)
, (1)
![]() . (2)
. (2)
в которых ![]() – количество входов
– количество входов ![]() -го нейрона,
-го нейрона, ![]() – сигналы, поступающие на вход
– сигналы, поступающие на вход ![]() -го нейрона (рисунок 3),
-го нейрона (рисунок 3), ![]() – его выходной сигнал,
– его выходной сигнал, ![]() – весовые коэффициенты (они же – силы синаптических связей), вычисляемые в результате обучения нейронной сети на обучающем множестве примеров.
– весовые коэффициенты (они же – силы синаптических связей), вычисляемые в результате обучения нейронной сети на обучающем множестве примеров.
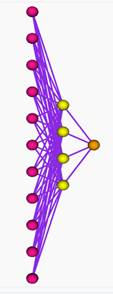
Рис. 1. Структура нейронной сети
После обучения прогностические свойства сети проверялись на тестирующих примерах. Результаты проверки представлены на рисунке 4, из которого видно, что полученные с помощью нейросети прогнозные значения таблицы НКЗ отличаются от фактических не более чем на 5,82%, что свидетельствует о том, что нейронная сеть, хотя и с небольшой погрешностью, но усвоила закономерности моделируемых процессов и что теперь эти закономерности можно изучать путем исследования полученной математической модели.

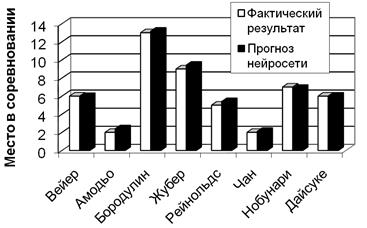
Рис. 4. Результат сопоставления фактического, заданного тестовым множеством, и прогнозного, полученного с помощью нейросети, результата – места в соревновании.
Результаты экспериментов и их обсуждение
Вычислительные эксперименты проводились с четырьмя потенциальными претендентами на победу в предстоящей зимней Олимпиаде-2014 в Сочи. Это: Евгений Плющенко, Патрик Чан, Джонни Вейер, Рейнольдс Кевин. Результат нейросетевого прогнозирования представлен на рисунке 5.
Выходной параметр нейронной сети кодирует результат соревнований – какое место займет претендент. Поэтому получившиеся значения ![]() , которые вычисляет нейронная сеть, можно расценивать как его шансы взойти на пьедестал. В дальнейшем этот выходной параметр нейросети мы иногда будем называть рейтингом спортсмена. Таким образом, анализируя результаты прогнозирования нейронной сети, изображенные на рис. 5, можно заключить, что на первое место наибольшие шансы имеет Патрик Чан, за второе и третье места борьба, по-видимому, развернется между Евгением Плющенко, Кевином Рейнольдсом и Джонни Вейером.
, которые вычисляет нейронная сеть, можно расценивать как его шансы взойти на пьедестал. В дальнейшем этот выходной параметр нейросети мы иногда будем называть рейтингом спортсмена. Таким образом, анализируя результаты прогнозирования нейронной сети, изображенные на рис. 5, можно заключить, что на первое место наибольшие шансы имеет Патрик Чан, за второе и третье места борьба, по-видимому, развернется между Евгением Плющенко, Кевином Рейнольдсом и Джонни Вейером.
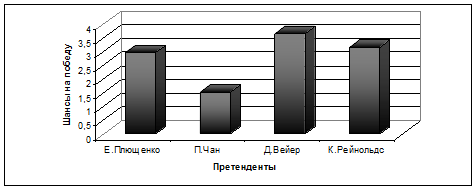
Рис. 5. Шансы претендентов на победу в Олимпиаде-2014
Как показывает мировой опыт, и в частности опыт Пермской научной школы искусственного интеллекта [2-6], применение методов нейросетевого математического моделирования позволяет не только предсказывать будущие события, но и проводить их исследования, ставить над моделями виртуальные компьютерные эксперименты и даже находить способы влияния на будущие события, корректировать их под свои желания и интересы. Так, изменяя входные параметры обученной нейронной сети и производя вычисления, можно получить ответы на многие вопросы. Например, изменяя возраст спортсмена и производя вычисления с помощью нейросети, можно проследить, как будут меняться его шансы на победу (рейтинг) с возрастом. Анализируя полученные таким образом кривые, изображенные на рисунке 6, можно заключить, что шансы на победу Е. Плющенко (даже с наличием травмы и возвращением на лед после нее) и П. Чана с возрастом будут постепенно падать. Шансы на победу Д. Вейера и К. Рейнольдса, наоборот, с увеличением их возраста будут возрастать.
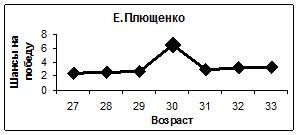
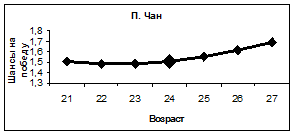
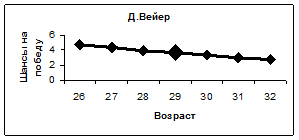
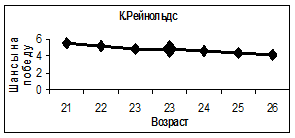
Рис. 6. Зависимость шансов на победу спортсменов от их возраста.
Маркером увеличенного размера отмечено состояние спортсмена на текущий момент времени
На рисунке 7 приведены результаты аналогичных компьютерных экспериментов, которые показывают, что виртуальное увеличение роста всех спортсменов приводит к уменьшению их рейтинга. Естественно, мы не можем рекомендовать спортсменам поменять их рост, но можно надеяться, что полученная методом математического моделирования закономерность может быть полезна для тренеров, например, при подборе кандидатов в будущие участники олимпийских игр.

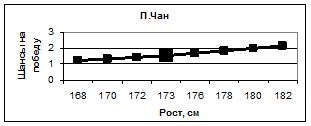
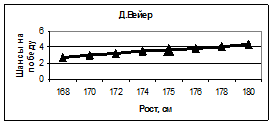
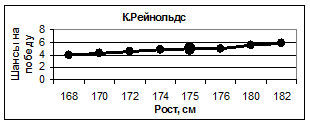
Рис. 7. Зависимость шансов на победу спортсменов от их роста
Изменяя вес спортсменов, производя вычисления с помощью нейросети, можно проследить, как зависят их шансы на победу от этого параметра. Полученные таким образом кривые, изображенные на рисунке 8, позволяют рекомендовать Е. Плющенко, П. Чану и Д. Вейеру для увеличения их шансов на победу сбавить вес, тогда как любые изменения веса К. Рейнольдса как в сторону уменьшения, так и в сторону увеличения отрицательно скажутся на его рейтинге.

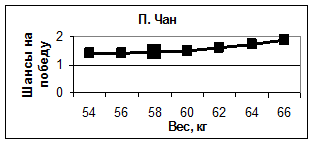
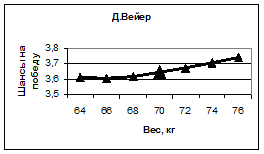
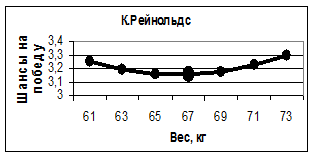
Рис. 8. Зависимость шансов на победу спортсменов от их веса
На рисунке 9 приведены кривые, показывающие зависимость рейтинга спортсменов от времени их начала занятий спортом. Анализируя эти кривые, можно заключить, что рейтинг К. Рейнольдса незначительно зависит от этого параметра, у П. Чана время оптимального начала занятий спортом (5 лет) совпадает с фактическим, как и у Д. Вейера, который встал на коньки в 11 лет, и у Е. Плющенко, начавшего тренировки в 4 года. Кривые, приведенные на этом рисунке, свидетельствуют также о том, что распространенное мнение «чем раньше встал ребенок на коньки – тем лучше для будущего спортсмена», является ошибочным. Наши вычисления показывают, что для каждого конкретного человека существует свой оптимальный период времени начала занятий тренировками.
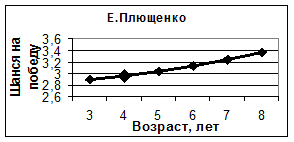
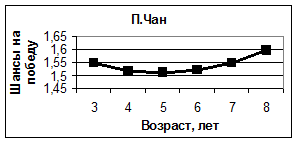
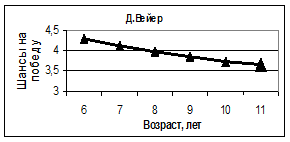
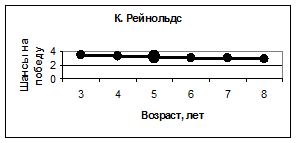
Рис. 9. Зависимость шанса на победу спортсменов от времени начала занятий спортом
Проводя целенаправленные исследования нейросетевой математической модели, можно разработать рекомендации – каким образом тому или иному спортсмену повысить его шансы на победу. Так, согласно результатам математического моделирования, представленным на рисунке 10, снижение веса на 1 кг, затем на 3 кг и на 4 кг приведет к заметному увеличению шансов на победу Е. Плющенко на 9%.
Согласно рисунку 11, снижение веса фигуриста П. Чана на 1 кг, а затем на 2 кг также приведет к увеличению его шансов на победу на 1,2%. Согласно рисунку 12, повышения шансов на победу на 25% может добиться фигурист Д. Вейер, если он снизит свой вес на 2 кг, повысит технику шагов, а затем повысит уровень вращения.
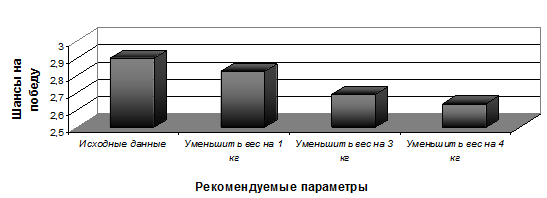
Рис. 10. Результаты моделирования влияния возможных изменений в физических данных Е. Плющенко на его рейтинг
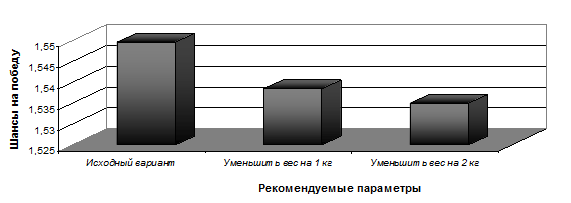
Рис. 11. Результаты моделирования влияния возможных изменений в физических данных П. Чана на его рейтинг
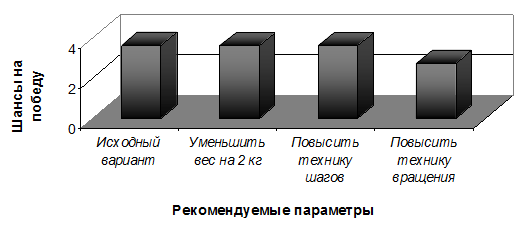
Рис. 12. Результаты моделирования влияния возможных изменений в физических данных Д. Вейера на его рейтинг
Согласно рис. 13, снижение веса Р. Кевина на 1 кг, повышение уровня базовых элементов (шага), а затем снижение веса на 2 кг приведут к увеличению его шансов на победу на 15%.
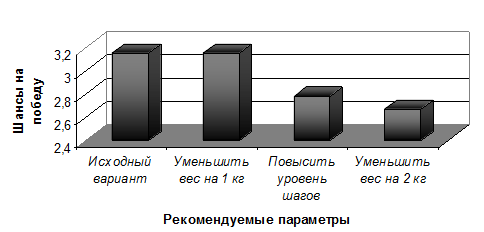
Рис. 13. Результаты моделирования влияния возможных изменений в физических данных Р. Кевина на его рейтинг
Заключение
1. Разработана нейросетевая математическая модель, предназначенная для прогнозирования шансов на победу в мужском одиночном фигурном катании на чемпионатах мира, Европы и олимпиадах. Показана ее адекватность.
2. С помощью математической модели определены шансы основных претендентов на победу в Олимпиаде-2014. Исследовано влияние некоторых параметров спортсменов на их спортивные результаты. Сделала попытка разработки рекомендаций по улучшению результативности каждого из рассмотренных спортсменов.
Рецензенты:
Русаков С.В., д.ф.-м.н., профессор, заведующий кафедрой прикладной математики и информатики, Пермский государственный национальный исследовательский университет, г.Пермь.
Пенский О.Г., д.т.н., доцент, профессор кафедры процессов управления и информационной безопасности, Пермский государственный национальный исследовательский университет, г.Пермь.



